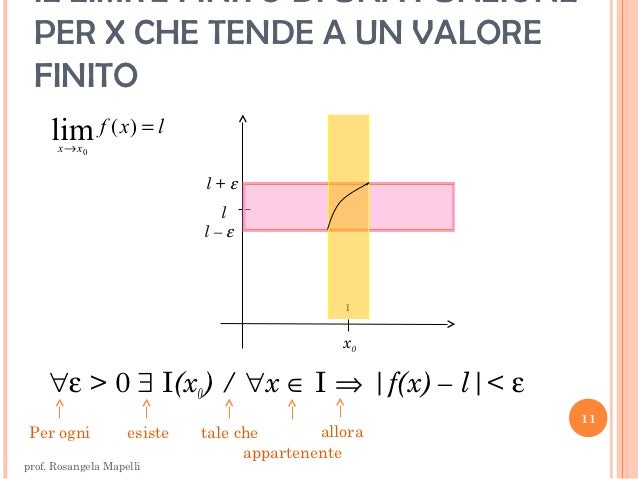
Limite Infinito Per X Che Tende A Un Valore Finito

Avete mai immaginato di avvicinarvi a un punto, infinitamente vicino, senza mai raggiungerlo? Questa è l'essenza del concetto di limite, un pilastro fondamentale del calcolo infinitesimale. In questo articolo, esploreremo un aspetto specifico: il limite infinito per x che tende a un valore finito. Il nostro obiettivo è rendere questo concetto accessibile a studenti delle scuole superiori e a chiunque voglia rafforzare le proprie basi matematiche.

Introduzione ai Limiti

Prima di tuffarci nell'infinito, ripassiamo brevemente cosa intendiamo per limite. In termini semplici, il limite di una funzione f(x) per x che tende a un valore c descrive il comportamento della funzione *quando* x si avvicina arbitrariamente a c, *senza* necessariamente essere uguale a c. Utilizziamo la notazione:

lim_x→c f(x) = L

Questo significa che, avvicinandoci a c, i valori di f(x) si avvicinano sempre di più a L. Ma cosa succede se, invece di avvicinarsi a un valore finito, f(x) cresce o decresce senza limiti?

Limiti Infiniti: Cosa Significa?

Un limite infinito si verifica quando, mentre x si avvicina a un valore c, i valori di f(x) diventano arbitrariamente grandi (positivi o negativi). In altre parole, f(x) "tende all'infinito" (positivo o negativo).

Usiamo una notazione simile, ma con il simbolo dell'infinito:

lim_x→c f(x) = +∞: f(x) cresce senza limiti positivamente.
lim_x→c f(x) = -∞: f(x) decresce senza limiti negativamente.

È cruciale capire che +∞ e -∞ *non* sono numeri reali. Rappresentano un comportamento: la funzione "esplode" in una direzione specifica.

Esempi Chiari e Accessibili

Vediamo alcuni esempi per chiarire il concetto. Consideriamo la funzione:

f(x) = 1/x

Cosa succede quando x si avvicina a 0? Analizziamo separatamente i due casi:

Avvicinandosi a 0 da destra (x > 0)

Immaginiamo x che assume valori sempre più piccoli e positivi: 0.1, 0.01, 0.001, e così via. Cosa succede a 1/x?

Se x = 0.1, 1/x = 10
Se x = 0.01, 1/x = 100
Se x = 0.001, 1/x = 1000

Chiaramente, 1/x diventa sempre più grande. Possiamo scrivere:

lim_x→0⁺ 1/x = +∞

Questo si legge: "Il limite di 1/x, per x che tende a 0 da destra, è più infinito".

Avvicinandosi a 0 da sinistra (x < 0)

Ora consideriamo x che assume valori sempre più piccoli e negativi: -0.1, -0.01, -0.001, e così via. Cosa succede a 1/x?

Se x = -0.1, 1/x = -10
Se x = -0.01, 1/x = -100
Se x = -0.001, 1/x = -1000

In questo caso, 1/x diventa sempre più piccolo (negativamente). Possiamo scrivere:

lim_x→0^- 1/x = -∞

Questo si legge: "Il limite di 1/x, per x che tende a 0 da sinistra, è meno infinito".

Asintoti Verticali

Quando una funzione ha un limite infinito in un punto c, la retta x = c è chiamata asintoto verticale. Nell'esempio di f(x) = 1/x, la retta x = 0 (l'asse y) è un asintoto verticale. La funzione si avvicina sempre di più a questa retta, senza mai toccarla.

Un Altro Esempio: f(x) = 1/x²

Consideriamo ora la funzione:

f(x) = 1/x²

Anche in questo caso, analizziamo cosa succede quando x si avvicina a 0. Notiamo che x² è sempre positivo (o zero).

Se x = 0.1, 1/x² = 100
Se x = -0.1, 1/x² = 100
Se x = 0.01, 1/x² = 10000
Se x = -0.01, 1/x² = 10000

Indipendentemente dal fatto che ci avviciniamo a 0 da destra o da sinistra, 1/x² diventa sempre più grande e positivo. Quindi:

lim_x→0 1/x² = +∞

Notate che *non* c'è bisogno di distinguere tra limite destro e sinistro in questo caso, perché entrambi tendono a +∞.

Perché Studiare i Limiti Infiniti?

Comprendere i limiti infiniti è fondamentale per diversi motivi:

Analisi del comportamento delle funzioni: Ci permette di capire come una funzione si comporta in prossimità di punti critici o all'infinito.
Studio degli asintoti: Ci aiuta a identificare gli asintoti di una funzione, che forniscono importanti informazioni sul suo grafico.
Calcolo delle derivate e degli integrali: I limiti sono alla base della definizione di derivata e integrale, concetti cruciali nel calcolo infinitesimale.
Applicazioni pratiche: I limiti infiniti trovano applicazione in vari campi, come la fisica (studio del comportamento di campi elettromagnetici), l'ingegneria (analisi di sistemi che tendono a una condizione di instabilità) e l'economia (modellizzazione di fenomeni con crescita esponenziale).

Come Affrontare Esercizi sui Limiti Infiniti

Ecco alcuni consigli pratici per affrontare esercizi che coinvolgono limiti infiniti:

Analisi del denominatore: Prestate particolare attenzione al denominatore di una frazione. Se il denominatore tende a zero mentre il numeratore tende a un valore diverso da zero, è probabile che il limite sia infinito.
Studio del segno: Determinate il segno del risultato (positivo o negativo) analizzando il segno del numeratore e del denominatore quando x si avvicina al valore limite.
Verifica dei limiti destro e sinistro: In molti casi, è necessario calcolare separatamente i limiti destro e sinistro per determinare se il limite esiste e qual è il suo valore.
Utilizzo di grafici: Tracciare il grafico della funzione può fornire un'intuizione visiva del suo comportamento e aiutare a confermare i risultati analitici.
Risoluzione di forme indeterminate: Talvolta ci si imbatte in forme indeterminate come "∞/∞" o "0/0". In questi casi, è necessario utilizzare tecniche algebriche (come la fattorizzazione o la razionalizzazione) o il teorema di L'Hôpital per semplificare l'espressione e calcolare il limite.

Esercizi Proposti

Mettete alla prova le vostre conoscenze con questi esercizi:

Calcolare: lim_x→2 1/(x-2)
Calcolare: lim_x→-3 (x+1)/(x+3)²
Determinare gli asintoti verticali della funzione f(x) = (x² - 4)/(x² - 1)

Conclusione

I limiti infiniti possono sembrare intimidatori all'inizio, ma con una comprensione chiara dei concetti e un po' di pratica, diventeranno uno strumento prezioso nel vostro arsenale matematico. Ricordate che l'infinito non è un numero, ma un'idea che descrive un comportamento senza limiti. Speriamo che questo articolo vi abbia fornito una solida base per esplorare ulteriormente questo affascinante argomento. Continuate a esercitarvi e a porvi domande: la matematica è un viaggio continuo di scoperta!