Leggi Orarie Moto Rettilineo Uniformemente Accelerato

Ciao! Hai mai osservato un'auto da corsa sfrecciare in accelerazione, oppure una pallina rotolare lungo un piano inclinato? Se la risposta è sì, allora hai già avuto un assaggio del Moto Rettilineo Uniformemente Accelerato (MRUA). Questo articolo è pensato per chiunque voglia capire a fondo questo concetto fondamentale della fisica, che siate studenti delle scuole superiori, appassionati di scienza o semplicemente curiosi di come funziona il mondo che ci circonda.

Il nostro obiettivo è rendere le leggi orarie del MRUA accessibili e intuitive, utilizzando esempi pratici e un linguaggio chiaro, evitando il gergo troppo tecnico. Preparati ad un viaggio nel mondo dell'accelerazione costante!

Cos'è il Moto Rettilineo Uniformemente Accelerato?

Immagina di essere su una bicicletta, su una strada perfettamente dritta, e di iniziare a pedalare aumentando costantemente la tua velocità. Questo è, in linea di massima, un MRUA. Tecnicamente, definiamo MRUA un moto che possiede le seguenti caratteristiche:

• Rettilineo: Il corpo si muove lungo una linea retta, senza cambiare direzione.
• Uniformemente Accelerato: L'accelerazione del corpo rimane costante nel tempo. Questo significa che la velocità aumenta (o diminuisce) sempre dello stesso valore in ogni intervallo di tempo uguale.

L'accelerazione è proprio la chiave di tutto. È la grandezza fisica che descrive quanto rapidamente la velocità di un oggetto cambia nel tempo. Si misura in metri al secondo quadrato (m/s²). Una accelerazione di 2 m/s² significa che la velocità aumenta di 2 metri al secondo ogni secondo.

Esempi di MRUA

Ecco alcuni esempi comuni di MRUA:

• Caduta libera (in assenza di attrito): Un oggetto che cade sotto l'influenza della sola forza di gravità (trascurando la resistenza dell'aria) sperimenta un'accelerazione costante, pari a circa 9.8 m/s² (l'accelerazione di gravità).
• Un'auto che accelera da ferma: Quando un'auto parte da ferma e aumenta la sua velocità in modo uniforme (con l'acceleratore premuto in modo costante), sta compiendo un MRUA.
• Un treno che frena in modo uniforme: Anche la decelerazione (un'accelerazione negativa) costante è un esempio di MRUA.

Le Leggi Orarie del MRUA: Descrivendo il Movimento

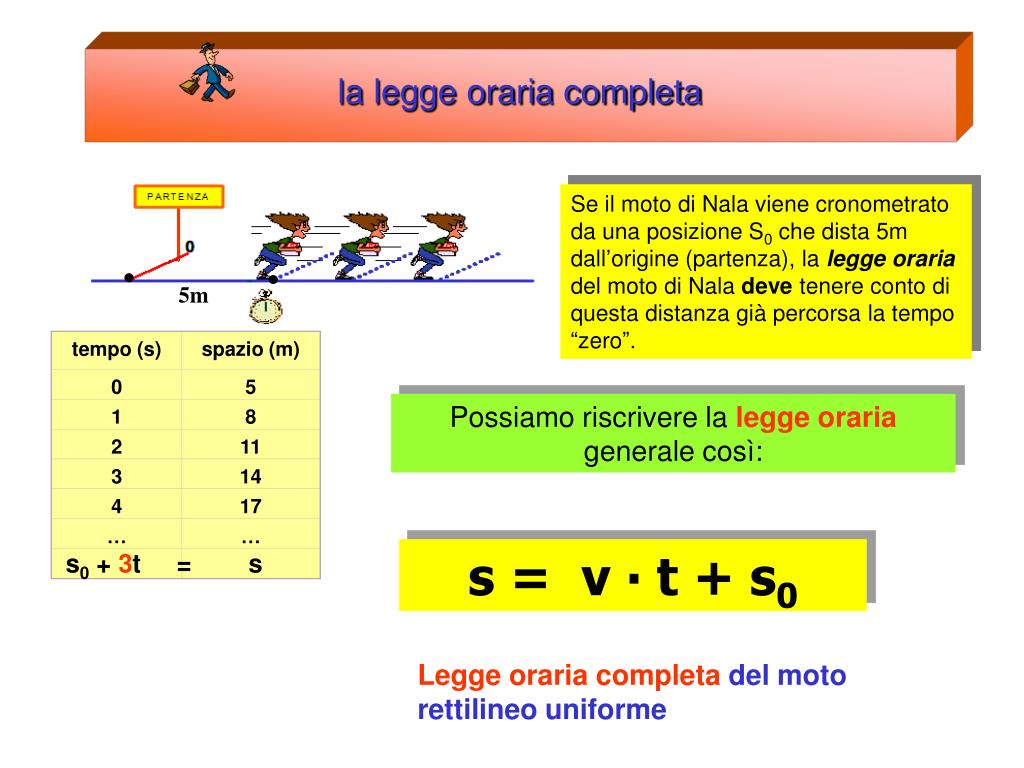
Le leggi orarie sono equazioni matematiche che descrivono la posizione, la velocità e l'accelerazione di un corpo in funzione del tempo. Nel caso del MRUA, queste leggi sono particolarmente semplici e potenti.

Consideriamo un corpo che si muove lungo una linea retta con un'accelerazione costante *a*. Definiamo inoltre:

• t: il tempo trascorso.
• v₀: la velocità iniziale del corpo (la velocità al tempo t=0).
• x₀: la posizione iniziale del corpo (la posizione al tempo t=0).
• v(t): la velocità del corpo al tempo *t*.
• x(t): la posizione del corpo al tempo *t*.

Con queste definizioni, possiamo enunciare le leggi orarie del MRUA:

1. Legge della Velocità

La velocità del corpo al tempo *t* è data da:

v(t) = v₀ + a * t

Questa equazione ci dice che la velocità al tempo *t* è uguale alla velocità iniziale *v₀* più l'incremento di velocità dovuto all'accelerazione *a* moltiplicata per il tempo trascorso *t*. In altre parole, la velocità aumenta (o diminuisce) linearmente con il tempo.

Esempio: Un'auto parte da ferma (v₀ = 0 m/s) con un'accelerazione di 3 m/s². Dopo 5 secondi, la sua velocità sarà:

v(5) = 0 + 3 * 5 = 15 m/s

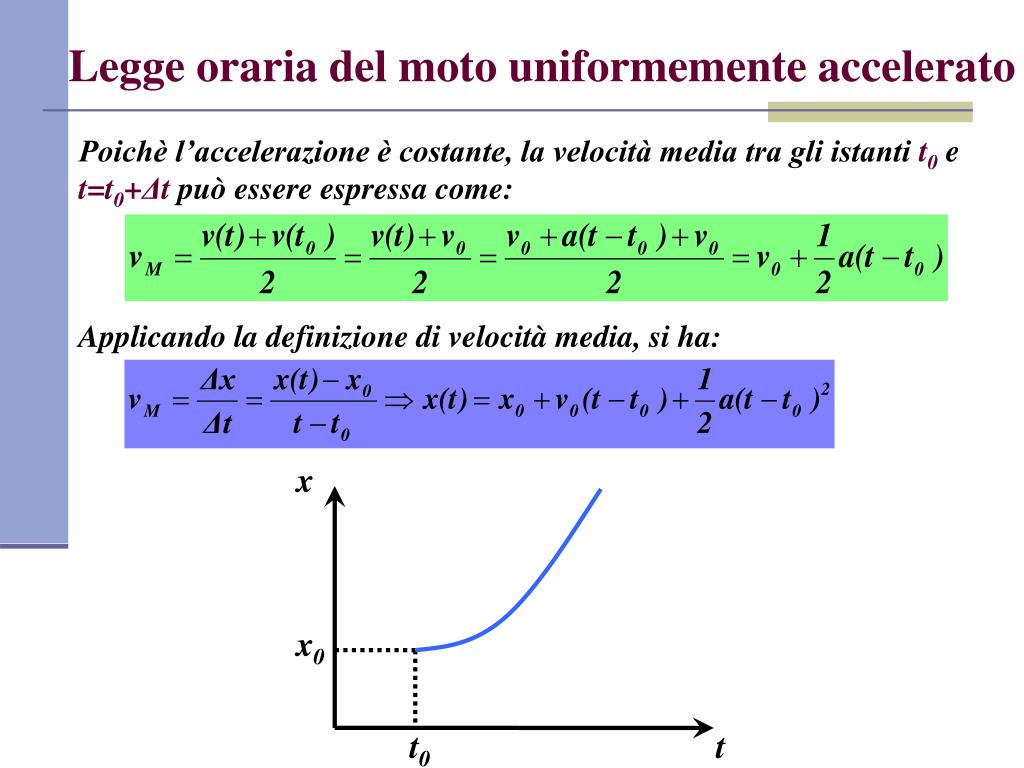
2. Legge della Posizione

La posizione del corpo al tempo *t* è data da:

x(t) = x₀ + v₀ * t + (1/2) * a * t²

Questa equazione è leggermente più complessa, ma ci dice che la posizione al tempo *t* è uguale alla posizione iniziale *x₀* più lo spostamento dovuto alla velocità iniziale *v₀* per il tempo *t*, più un termine quadratico che tiene conto dell'accelerazione *a*.

Esempio: Un ciclista parte da una posizione x₀ = 2 metri con una velocità iniziale v₀ = 4 m/s e accelera a 1 m/s². Dopo 3 secondi, la sua posizione sarà:

x(3) = 2 + 4 * 3 + (1/2) * 1 * 3² = 2 + 12 + 4.5 = 18.5 metri

3. Equazione di Torricelli

Esiste una terza equazione, derivata dalle prime due, molto utile quando non conosciamo il tempo ma conosciamo la velocità iniziale, la velocità finale, l'accelerazione e lo spostamento. Questa è l'Equazione di Torricelli:

v² = v₀² + 2 * a * (x - x₀)

Dove *v* è la velocità finale, *v₀* è la velocità iniziale, *a* è l'accelerazione e (x - x₀) è lo spostamento.

Esempio: Un aereo decolla da fermo (v₀ = 0 m/s) e accelera con un'accelerazione di 5 m/s² fino a raggiungere una velocità di decollo di 80 m/s. Qual è la lunghezza minima della pista necessaria?

Usando l'equazione di Torricelli, possiamo ricavare lo spostamento (x - x₀):

80² = 0² + 2 * 5 * (x - x₀)

6400 = 10 * (x - x₀)

(x - x₀) = 640 metri

Quindi, la pista deve essere lunga almeno 640 metri.

Come Usare le Leggi Orarie nella Pratica

Ora che conosciamo le leggi orarie, vediamo come possiamo utilizzarle per risolvere problemi pratici:

1. Identifica il tipo di moto: Assicurati che il problema descriva effettivamente un MRUA (moto rettilineo con accelerazione costante).
2. Definisci un sistema di riferimento: Scegli un'origine e una direzione positiva. Questo ti aiuterà a definire i segni delle grandezze fisiche (posizione, velocità, accelerazione).
3. Scrivi i dati del problema: Annota tutti i valori noti (v₀, x₀, *a*, *t*, ecc.) e identifica le incognite (cosa devi calcolare).
4. Scegli la legge oraria appropriata: Se devi calcolare la velocità, usa la legge della velocità. Se devi calcolare la posizione, usa la legge della posizione. Se non hai il tempo, usa l'equazione di Torricelli.
5. Risolvi l'equazione: Sostituisci i valori noti nell'equazione e risolvi per l'incognita.
6. Verifica il risultato: Controlla che il risultato abbia senso fisicamente e che le unità di misura siano corrette.

Un Esempio Complesso: Inseguimento

Un poliziotto, fermo ad un semaforo, vede passare un'auto che supera il limite di velocità a 25 m/s. Il poliziotto parte all'inseguimento con un'accelerazione costante di 2 m/s². Quanto tempo impiega il poliziotto per raggiungere l'auto e a che distanza dal semaforo avviene l'inseguimento?

Analisi: Abbiamo due oggetti in MRUA: l'auto (con accelerazione zero, quindi moto rettilineo uniforme) e il poliziotto. Vogliamo trovare il tempo *t* in cui le loro posizioni sono uguali.

Auto:

• v_0,auto = 25 m/s
• a_auto = 0 m/s²
• x_0,auto = 0 m (assumiamo che il semaforo sia l'origine)
• x_auto(t) = 0 + 25t + (1/2)*0*t² = 25t

Poliziotto:

• v_0,pol = 0 m/s
• a_pol = 2 m/s²
• x_0,pol = 0 m
• x_pol(t) = 0 + 0*t + (1/2)*2*t² = t²

Inseguimento: Le posizioni sono uguali quando:

x_auto(t) = x_pol(t)

25t = t²

t² - 25t = 0

t(t - 25) = 0

Le soluzioni sono t = 0 (il momento in cui l'auto passa il poliziotto) e t = 25 secondi. Quindi, il poliziotto raggiunge l'auto dopo 25 secondi.

La distanza dal semaforo è:

x_auto(25) = 25 * 25 = 625 metri

x_pol(25) = 25² = 625 metri

L'inseguimento avviene a 625 metri dal semaforo.

Oltre la Teoria: Il MRUA nel Mondo Reale

Le leggi del MRUA non sono solo formule astratte. Sono fondamentali per comprendere e prevedere il comportamento di molti sistemi fisici. Gli ingegneri le utilizzano per progettare automobili, aerei, montagne russe e molto altro. I fisici le usano per studiare il movimento dei proiettili, la caduta dei corpi e molti altri fenomeni.

Pensate a quanto sia importante conoscere l'accelerazione di un'auto per calcolare lo spazio di frenata necessario per evitare un incidente. Oppure, immaginate di dover calcolare la traiettoria di un missile: la precisione è fondamentale, e le leggi del MRUA (insieme a concetti più avanzati) sono alla base di questi calcoli.

Comprendere il MRUA ti fornisce una base solida per affrontare concetti più complessi della fisica, come il moto parabolico, il moto circolare e la dinamica. È un tassello fondamentale per comprendere come funziona il mondo che ci circonda.

Conclusione

In questo articolo, abbiamo esplorato in dettaglio il Moto Rettilineo Uniformemente Accelerato (MRUA), definendo cos'è, presentando le sue leggi orarie e mostrando come applicarle a problemi pratici. Spero che questo viaggio nel mondo dell'accelerazione costante ti sia stato utile e ti abbia fornito una solida base per approfondire ulteriormente i tuoi studi di fisica.

Ricorda: la fisica non è solo un insieme di formule, ma un modo per comprendere e interpretare il mondo che ci circonda. Continua ad esplorare, a sperimentare e a porre domande! La conoscenza è la chiave per sbloccare i segreti dell'universo.