Lato Obliquo Parallelogramma Conoscendo Base E Altezza

Capita spesso di trovarsi di fronte a problemi di geometria, soprattutto quando si tratta di calcolare aree. In questo articolo, affronteremo un caso specifico: come calcolare l'area di un parallelogramma obliquo quando conosciamo la base e l'altezza. Potrebbe sembrare complicato, ma vedremo che con un po' di chiarezza e le formule giuste, diventa un'operazione semplice.

Molti studenti si bloccano di fronte a figure geometriche "strane", come il parallelogramma obliquo, che differisce dal rettangolo per l'assenza di angoli retti. La paura di sbagliare, la mancanza di una comprensione solida dei concetti di base, o semplicemente l'ansia da compito in classe possono rendere l'apprendimento un'esperienza frustrante. Cercheremo di superare queste difficoltà insieme, passo dopo passo.

Cos'è un Parallelogramma Obliquo?

Prima di addentrarci nel calcolo dell'area, definiamo cos'è esattamente un parallelogramma obliquo. Immagina un rettangolo che viene "spinto" lateralmente. I suoi lati opposti rimangono paralleli, ma gli angoli non sono più retti (90 gradi). Questa è la chiave: lati opposti paralleli e angoli non retti.

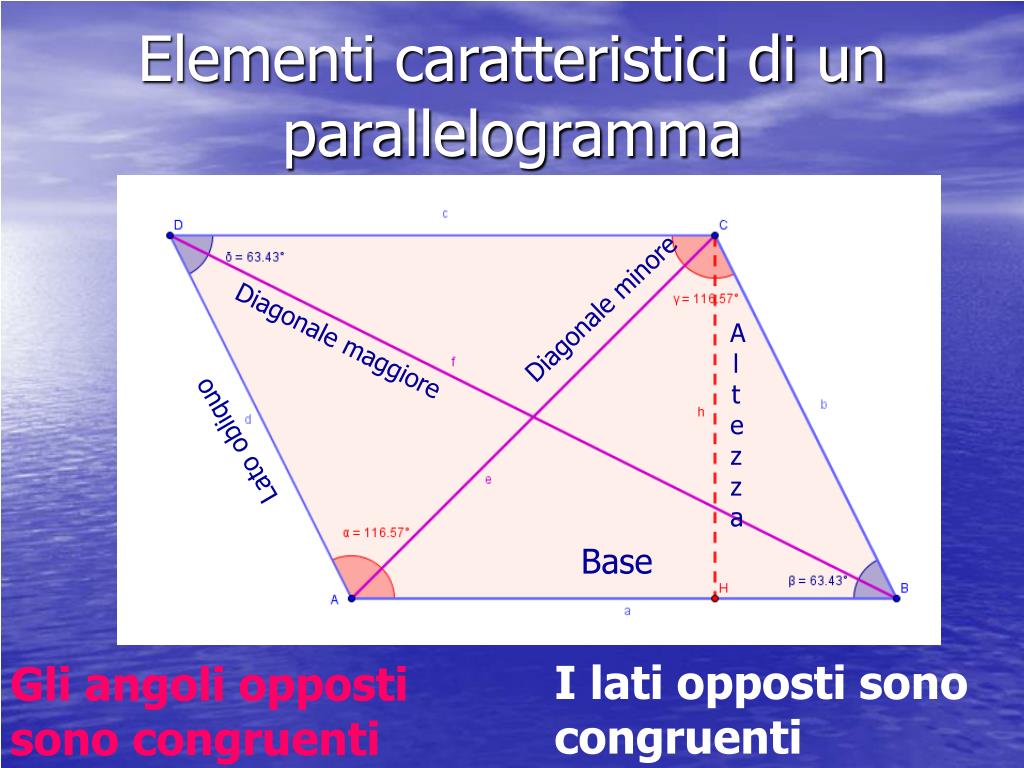
Ecco le caratteristiche principali:

Quattro lati.
Lati opposti paralleli.
Angoli opposti uguali.
Angoli adiacenti supplementari (la loro somma fa 180 gradi).
Le diagonali si intersecano nel loro punto medio.

Differenza tra Parallelogramma Obliquo e Rettangolo

La differenza fondamentale, come già accennato, è l'angolo. Un rettangolo ha quattro angoli retti. Il parallelogramma obliquo no. Questo significa che non possiamo semplicemente moltiplicare la lunghezza di due lati adiacenti per trovare l'area, come faremmo con un rettangolo.

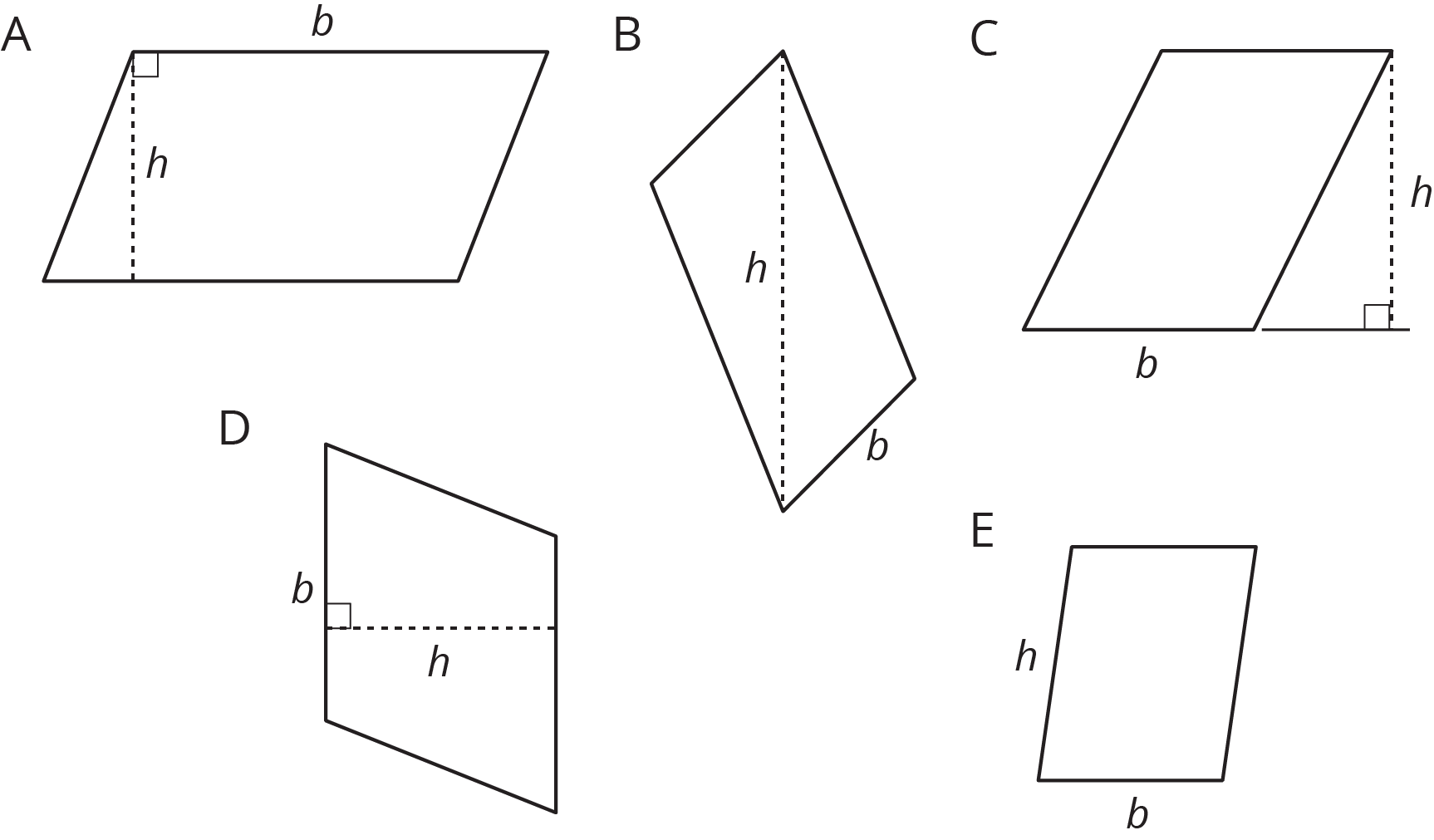
Il Concetto di Altezza in un Parallelogramma Obliquo

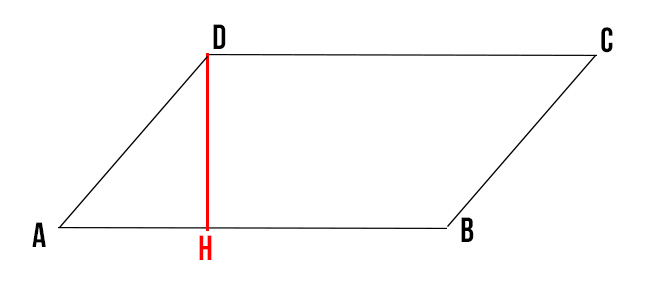
L'altezza è un concetto cruciale. Non è la lunghezza di uno dei lati obliqui! L'altezza è la distanza perpendicolare tra la base e il lato opposto. Immagina di tracciare una linea retta (formando un angolo di 90 gradi) dalla base al lato opposto. Quella linea è l'altezza.

Visualizzare l'altezza può essere un po' complicato. Pensa ad una goccia di pioggia che cade verticalmente sulla base del parallelogramma. La distanza che percorre la goccia fino a raggiungere la base è l'altezza.

Calcolo dell'Area: La Formula Magica

Ora arriviamo al punto cruciale: come calcolare l'area di questo parallelogramma obliquo. La formula è sorprendentemente semplice:

Area = Base x Altezza

Sì, è tutto qui! È la stessa formula che useresti per un rettangolo, solo che devi assicurarti di usare l'altezza corretta, quella perpendicolare alla base.

Esempio Pratico

Supponiamo di avere un parallelogramma obliquo con una base di 10 cm e un'altezza di 5 cm. L'area sarebbe:

Area = 10 cm x 5 cm = 50 cm²

Quindi, l'area del parallelogramma è di 50 centimetri quadrati.

Come Trovare l'Altezza se Non è Data

A volte, il problema non ti fornisce direttamente l'altezza. Potrebbe darti la lunghezza di un lato obliquo e l'angolo tra quel lato e la base. In questo caso, dobbiamo ricorrere alla trigonometria, in particolare alla funzione seno.

Se conosciamo l'angolo (α) tra la base e il lato obliquo (l), possiamo calcolare l'altezza (h) usando la seguente formula:

h = l x sin(α)

Dove:

h = altezza
l = lunghezza del lato obliquo
α = angolo tra la base e il lato obliquo
sin(α) = seno dell'angolo α

Esempio con Trigonometria

Supponiamo di avere un parallelogramma con una base di 12 cm, un lato obliquo di 8 cm, e l'angolo tra la base e il lato obliquo è di 30 gradi. Dobbiamo prima calcolare l'altezza:

h = 8 cm x sin(30°) = 8 cm x 0.5 = 4 cm

Ora che abbiamo l'altezza, possiamo calcolare l'area:

Area = 12 cm x 4 cm = 48 cm²

L'area del parallelogramma è quindi di 48 centimetri quadrati.

Controindicazioni e Aspetti da Considerare

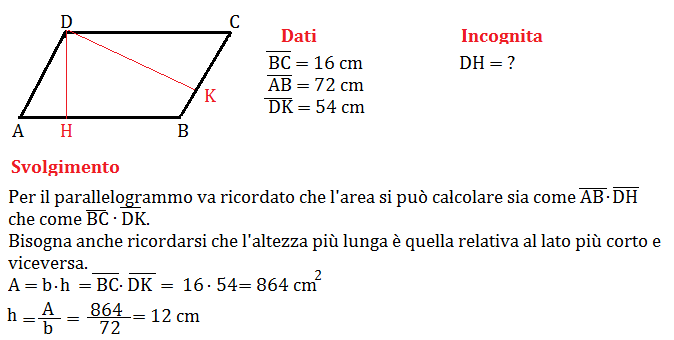
Alcune persone potrebbero obiettare che questo metodo funziona solo se conosciamo la base e l'altezza "corrette". È vero! L'importante è identificare la base e l'altezza che sono perpendicolari tra loro. Possiamo scegliere qualsiasi lato come base, ma l'altezza deve essere la distanza perpendicolare tra quel lato e il suo lato opposto.

Un altro punto da considerare è l'importanza delle unità di misura. Assicurati che la base e l'altezza siano espresse nella stessa unità (ad esempio, entrambe in centimetri). Altrimenti, dovrai convertire una delle due misure prima di calcolare l'area.

Applicazioni Pratiche

Capire come calcolare l'area di un parallelogramma obliquo non è solo un esercizio accademico. Ha diverse applicazioni pratiche:

Architettura: Nel design di edifici e strutture, forme parallelogrammiche possono essere utilizzate per creare effetti visivi interessanti o per adattarsi a vincoli specifici del terreno.
Ingegneria: Nel calcolo delle forze su strutture inclinate, la comprensione delle proprietà dei parallelogrammi è fondamentale.
Design: Nel design grafico e nell'arte, i parallelogrammi obliqui possono essere utilizzati per creare composizioni dinamiche e interessanti.
Matematica e Fisica: La scomposizione di vettori spesso utilizza la rappresentazione di forze come lati di un parallelogramma.

Consigli e Strategie per la Risoluzione dei Problemi

Ecco alcuni consigli per affrontare i problemi che coinvolgono il calcolo dell'area di un parallelogramma obliquo:

Disegna sempre un diagramma: Visualizzare il problema ti aiuterà a capire meglio le relazioni tra i lati, gli angoli e l'altezza.
Identifica la base e l'altezza: Assicurati di utilizzare l'altezza perpendicolare alla base che hai scelto.
Se necessario, usa la trigonometria: Se non ti viene data l'altezza, utilizza le funzioni trigonometriche (seno, coseno, tangente) per calcolarla.
Verifica le unità di misura: Assicurati che tutte le misure siano espresse nella stessa unità.
Controlla il tuo lavoro: Una volta calcolata l'area, ricontrolla i tuoi calcoli per evitare errori.

In Sintesi: La Chiave del Successo

Calcolare l'area di un parallelogramma obliquo non è poi così difficile. Ricorda la formula fondamentale (Area = Base x Altezza) e assicurati di usare l'altezza corretta (la distanza perpendicolare tra la base e il lato opposto). Se necessario, usa la trigonometria per calcolare l'altezza. Con un po' di pratica, diventerai un esperto nel calcolo delle aree di parallelogrammi obliqui!

Speriamo che questo articolo ti sia stato utile. La matematica non deve essere una barriera, ma uno strumento per comprendere meglio il mondo che ci circonda. Prenditi il tempo per esplorare, sperimentare e non aver paura di fare domande.

Ora, ti invito a riflettere: come potresti applicare questa conoscenza nella tua vita quotidiana o in un progetto che stai realizzando?