L'altezza Di Un Triangolo Equilatero è Uguale Al Lato

Ti sei mai trovato di fronte a un problema di geometria, fissando un triangolo equilatero e chiedendoti come calcolare la sua altezza? Non sei solo! Molti si bloccano di fronte a questa sfida, soprattutto se non hanno a portata di mano la formula giusta. La buona notizia è che capire la relazione tra l'altezza e il lato di un triangolo equilatero è più semplice di quanto sembri, e una volta compresa, ti aprirà un mondo di possibilità nella risoluzione dei problemi geometrici.
Questo articolo è qui per guidarti passo dopo passo attraverso il processo, rendendo la geometria accessibile e persino divertente. Dimentica le formule astratte e le spiegazioni complicate: ti forniremo un approccio chiaro, pratico e pieno di esempi per padroneggiare questo concetto fondamentale. Preparati a svelare i segreti del triangolo equilatero!
Cos'è un Triangolo Equilatero?
Prima di addentrarci nel calcolo dell'altezza, ripassiamo brevemente cosa definisce un triangolo equilatero. Un triangolo equilatero è un triangolo con tre lati uguali. Di conseguenza, anche tutti e tre gli angoli sono uguali e misurano 60 gradi ciascuno. Questa simmetria rende il triangolo equilatero una figura geometrica particolarmente elegante e, per fortuna, piuttosto semplice da gestire.
Pensa a una fetta di torta perfettamente divisa in tre parti uguali. Ogni fetta ha la forma di un triangolo equilatero. Questa immagine ti aiuterà a visualizzare le proprietà di questa figura.
L'Altezza di un Triangolo: Una Definizione
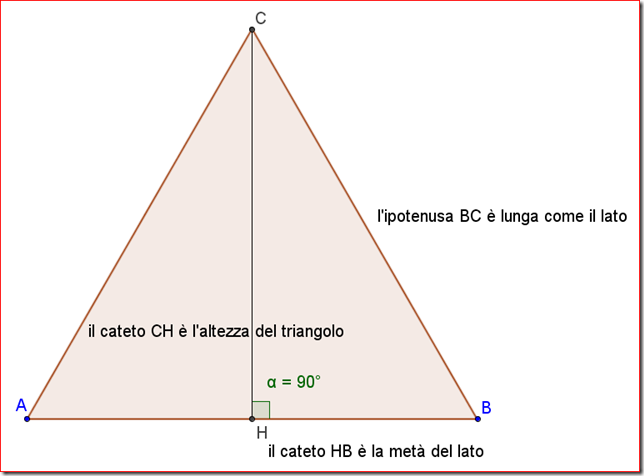
L'altezza di un triangolo è un segmento di retta perpendicolare che va da un vertice al lato opposto (o al prolungamento del lato opposto). In un triangolo equilatero, l'altezza ha una proprietà speciale: divide il triangolo in due triangoli rettangoli congruenti. Questo è un punto cruciale per capire la relazione tra l'altezza e il lato.
Immagina di tracciare una linea dritta dal vertice superiore del tuo triangolo equilatero fino al punto medio del lato inferiore. Quella linea è l'altezza. Nota come ha creato due triangoli più piccoli, entrambi con un angolo retto.
La Relazione Fondamentale: Altezza e Lato
Ed ecco la magia: l'altezza di un triangolo equilatero è strettamente legata alla lunghezza del suo lato. La formula che descrive questa relazione è la seguente:
Altezza (h) = (Lato (l) * √3) / 2
Dove:
* h rappresenta l'altezza del triangolo. * l rappresenta la lunghezza di un lato del triangolo. * √3 rappresenta la radice quadrata di 3 (circa 1.732).Questa formula deriva dal teorema di Pitagora, applicato a uno dei triangoli rettangoli formati dall'altezza. Possiamo visualizzare il triangolo equilatero diviso in due triangoli rettangoli. L'altezza è un cateto, metà del lato è l'altro cateto, e il lato del triangolo equilatero è l'ipotenusa.
In altre parole, l'altezza di un triangolo equilatero è sempre circa 0.866 volte la lunghezza del suo lato. Questa è una costante importante da ricordare!
Come Derivare la Formula (Per i Più Curiosi)
Se sei curioso di sapere da dove viene questa formula, ecco una breve spiegazione basata sul teorema di Pitagora:
1. Considera un triangolo equilatero con lato 'l'. Traccia l'altezza 'h' che divide il triangolo in due triangoli rettangoli.
2. Ogni triangolo rettangolo ha un'ipotenusa di lunghezza 'l', un cateto di lunghezza 'h' (l'altezza) e un altro cateto di lunghezza 'l/2' (metà del lato).
3. Applica il teorema di Pitagora: a² + b² = c² dove a = h, b = l/2, e c = l.
4. Quindi: h² + (l/2)² = l²
5. Risolvi per h²: h² = l² - (l/2)² = l² - l²/4 = (3/4)l²
6. Prendi la radice quadrata di entrambi i lati: h = √(3/4)l² = (√3/2)l
Ecco! Abbiamo derivato la formula dell'altezza di un triangolo equilatero.
Esempi Pratici: Mettiamoci al Lavoro!
Per rendere il tutto più concreto, vediamo alcuni esempi pratici:
Esempio 1: Supponiamo di avere un triangolo equilatero con un lato di 10 cm. Qual è la sua altezza?
Applichiamo la formula: h = (10 cm * √3) / 2 ≈ (10 cm * 1.732) / 2 ≈ 8.66 cm.
Quindi, l'altezza del triangolo è circa 8.66 cm.
Esempio 2: Se l'altezza di un triangolo equilatero è 5 cm, qual è la lunghezza del suo lato?
Questa volta, dobbiamo riorganizzare la formula: l = (2 * h) / √3 = (2 * 5 cm) / 1.732 ≈ 5.77 cm.
Quindi, la lunghezza del lato del triangolo è circa 5.77 cm.
Perché è Importante Conoscere Questa Relazione?
Capire la relazione tra l'altezza e il lato di un triangolo equilatero è fondamentale per risolvere una varietà di problemi geometrici. Questa conoscenza ti permette di:
* Calcolare l'area di un triangolo equilatero (Area = (base * altezza) / 2). * Determinare le dimensioni di un triangolo equilatero conoscendo solo un lato o l'altezza. * Risolvere problemi di trigonometria più complessi. * Applicare questi concetti in contesti pratici come l'architettura, l'ingegneria e il design.Consigli Utili per Ricordare la Formula
Ecco alcuni trucchi per ricordare facilmente la formula:
* Visualizzazione: Immagina sempre il triangolo equilatero diviso in due triangoli rettangoli. * Mnemonico: Crea una frase memorabile che ti aiuti a ricordare la formula (ad esempio, "L'altezza è lato per radice di tre diviso due"). * Pratica: Risolvi molti esercizi per familiarizzare con la formula e le sue applicazioni. * Derivazione: Comprendere la derivazione della formula (attraverso il teorema di Pitagora) ti aiuterà a ricordarla meglio.Applicazioni nel Mondo Reale
I triangoli equilateri, e quindi la comprensione della relazione tra i loro lati e l'altezza, si trovano ovunque intorno a noi. Considera le seguenti applicazioni:
* Architettura: Molte strutture architettoniche utilizzano triangoli equilateri per la loro stabilità e resistenza. Pensiamo a ponti, cupole e telai di edifici. * Ingegneria: Gli ingegneri utilizzano triangoli equilateri nella progettazione di componenti meccanici e strutturali. * Design: I triangoli equilateri sono spesso utilizzati in design grafici, loghi e modelli tessili per la loro estetica piacevole. * Natura: Le forme triangolari si trovano in natura, ad esempio nelle strutture cristalline e nelle celle dei favi.Conclusione
Speriamo che questo articolo ti abbia aiutato a comprendere la relazione tra l'altezza e il lato di un triangolo equilatero. Ricorda la formula: Altezza = (Lato * √3) / 2. Pratica con gli esempi e non aver paura di applicare questa conoscenza a problemi più complessi.
La geometria può sembrare intimidatoria all'inizio, ma con la giusta guida e un po' di pratica, può diventare uno strumento potente per comprendere e risolvere problemi nel mondo che ci circonda. Ora, vai e conquista il mondo dei triangoli equilateri!