La Prova Del 9 Come Si Fa

Ti sei mai trovato a fare un lungo calcolo, magari durante un esame o mentre bilanciavi il budget familiare, e ti sei chiesto se il risultato fosse corretto? Esiste un metodo rapido e affascinante per verificare la correttezza di operazioni aritmetiche: è la prova del nove. Questo articolo è pensato per te, studente, professionista o semplicemente curioso, che desideri apprendere o rispolverare questa tecnica matematica antica e utile. Impareremo insieme come applicarla in modo semplice ed efficace.

Cos'è la Prova del Nove?

La prova del nove è un metodo rapido per controllare se un'operazione aritmetica (addizione, sottrazione, moltiplicazione e divisione) è probabilmente corretta. Attenzione all'avverbio "probabilmente": non è una garanzia assoluta, ma fornisce un'indicazione forte. Si basa sul concetto dei resti modulo 9 e sfrutta le proprietà della divisibilità per 9.

In sostanza, trasformiamo i numeri coinvolti nell'operazione in cifre singole (tra 0 e 9) sommandone le cifre ripetutamente fino a ottenere un'unica cifra. Queste cifre vengono poi usate per ricreare l'operazione originale, ma con numeri molto più piccoli. Se il risultato ottenuto con queste cifre ridotte corrisponde al risultato ridotto dell'operazione originale, allora l'operazione è probabilmente corretta.

A Chi è Utile la Prova del Nove?

La prova del nove è particolarmente utile a:

• Studenti: Per controllare i compiti a casa e durante gli esami, evitando errori banali.
• Contabili e Commercialisti: Per una verifica rapida di calcoli complessi e bilanci.
• Chiunque faccia calcoli a mano: Per avere una conferma immediata della correttezza del risultato.

Come Si Fa la Prova del Nove: Passo Passo

Vediamo ora come applicare la prova del nove a ciascuna delle quattro operazioni aritmetiche fondamentali.

Addizione

Supponiamo di voler verificare se l'addizione 345 + 678 = 1023 è corretta.

1. Calcola il resto modulo 9 per ogni addendo:
   • Per 345: 3 + 4 + 5 = 12. Poiché 12 è maggiore di 9, sommiamo di nuovo: 1 + 2 = 3. Il resto modulo 9 di 345 è 3.
   • Per 678: 6 + 7 + 8 = 21. 2 + 1 = 3. Il resto modulo 9 di 678 è 3.
2. Calcola il resto modulo 9 della somma:
   • Per 1023: 1 + 0 + 2 + 3 = 6. Il resto modulo 9 di 1023 è 6.
3. Verifica: Somma i resti modulo 9 degli addendi (3 + 3 = 6) e confrontalo con il resto modulo 9 della somma (6). In questo caso, 6 = 6, quindi l'addizione è probabilmente corretta.

Esempio pratico:

Immagina di dover sommare il costo di diversi articoli al supermercato: 125€ + 34€ + 87€ = 246€. Applichiamo la prova del nove:

• 125: 1 + 2 + 5 = 8
• 34: 3 + 4 = 7
• 87: 8 + 7 = 15 -> 1 + 5 = 6
• 246: 2 + 4 + 6 = 12 -> 1 + 2 = 3

Ora sommiamo i resti degli addendi: 8 + 7 + 6 = 21 -> 2 + 1 = 3. Il risultato (3) corrisponde al resto della somma (3). La somma è probabilmente corretta.

Sottrazione

Supponiamo di voler verificare se la sottrazione 987 - 456 = 531 è corretta.

1. Calcola il resto modulo 9 per il minuendo e il sottraendo:
   • Per 987: 9 + 8 + 7 = 24. 2 + 4 = 6.
   • Per 456: 4 + 5 + 6 = 15. 1 + 5 = 6.
2. Calcola il resto modulo 9 della differenza:
   • Per 531: 5 + 3 + 1 = 9. Poiché 9 è divisibile per 9, il resto modulo 9 è 0.
3. Verifica: Sottrai il resto modulo 9 del sottraendo dal resto modulo 9 del minuendo (6 - 6 = 0) e confrontalo con il resto modulo 9 della differenza (0). In questo caso, 0 = 0, quindi la sottrazione è probabilmente corretta.
4. Caso particolare: Se il risultato della sottrazione dei resti fosse negativo, aggiungi 9 al risultato finché non diventa positivo. Ad esempio, se avessimo ottenuto -2, avremmo aggiunto 9 per ottenere 7.

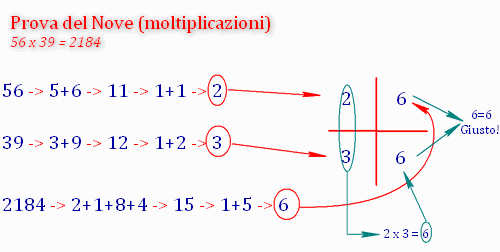
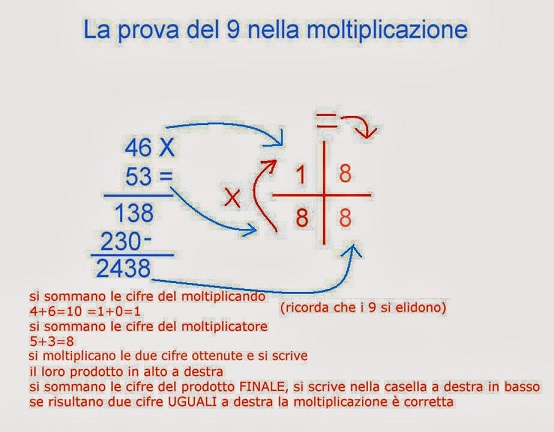
Moltiplicazione

Supponiamo di voler verificare se la moltiplicazione 123 x 45 = 5535 è corretta.

1. Calcola il resto modulo 9 per i due fattori:
   • Per 123: 1 + 2 + 3 = 6.
   • Per 45: 4 + 5 = 9. Il resto modulo 9 è 0.
2. Calcola il resto modulo 9 del prodotto:
   • Per 5535: 5 + 5 + 3 + 5 = 18. 1 + 8 = 9. Il resto modulo 9 è 0.
3. Verifica: Moltiplica i resti modulo 9 dei fattori (6 x 0 = 0) e confrontalo con il resto modulo 9 del prodotto (0). In questo caso, 0 = 0, quindi la moltiplicazione è probabilmente corretta.

Ricorda: qualsiasi numero moltiplicato per 0 dà come risultato 0. Quindi, se uno dei fattori ha resto 0, anche il prodotto dovrà avere resto 0 per essere considerato probabilmente corretto.

Divisione

La prova del nove nella divisione è un po' più complessa, ma comunque fattibile. Supponiamo di voler verificare se la divisione 789 ÷ 3 = 263 è corretta.

1. Verifica che la divisione sia senza resto. Se c'è un resto, la prova del nove va adattata (vedi esempio successivo).
2. Calcola il resto modulo 9 per il divisore e il quoziente:
   • Per 3: Il resto modulo 9 è 3.
   • Per 263: 2 + 6 + 3 = 11. 1 + 1 = 2.
3. Calcola il resto modulo 9 del dividendo:
   • Per 789: 7 + 8 + 9 = 24. 2 + 4 = 6.
4. Verifica: Moltiplica il resto modulo 9 del divisore per il resto modulo 9 del quoziente (3 x 2 = 6) e confrontalo con il resto modulo 9 del dividendo (6). In questo caso, 6 = 6, quindi la divisione è probabilmente corretta.

Divisione con resto:

Supponiamo di voler verificare se 800 ÷ 7 = 114 con resto 2 è corretta.

1. Calcola il resto modulo 9 per il divisore e il quoziente:
   • Per 7: Il resto modulo 9 è 7.
   • Per 114: 1 + 1 + 4 = 6.
2. Calcola il resto modulo 9 del dividendo:
   • Per 800: 8 + 0 + 0 = 8.
3. Verifica: Moltiplica il resto modulo 9 del divisore per il resto modulo 9 del quoziente (7 x 6 = 42). Poi calcola il resto di questo risultato (4 + 2 = 6). Infine, somma il resto della divisione (2) al resto ottenuto (6 + 2 = 8). Confronta questo risultato con il resto modulo 9 del dividendo (8). In questo caso, 8 = 8, quindi la divisione è probabilmente corretta.

Perché Funziona la Prova del Nove?

La prova del nove funziona perché si basa sulle proprietà dei resti modulo 9. In breve, il resto della divisione di un numero per 9 è uguale al resto della divisione per 9 della somma delle sue cifre. Questo si basa sul fatto che 10 è congruo a 1 modulo 9 (cioè, 10 - 1 è divisibile per 9). Quindi, qualsiasi potenza di 10 è anch'essa congrua a 1 modulo 9. Questo ci permette di ridurre un numero alla somma delle sue cifre senza alterarne il resto modulo 9.

Limitazioni della Prova del Nove

Come accennato all'inizio, la prova del nove non è infallibile. Ha alcune limitazioni importanti:

• Non rileva errori che siano multipli di 9: Ad esempio, se hai scambiato due cifre consecutive, la prova del nove non lo rileverà, perché la somma delle cifre rimane la stessa. Per esempio: 123 + 456 = 579; se scrivessimo 123 + 456 = 570, la prova del nove non segnalerebbe l'errore perché la somma delle cifre di 579 (21 -> 3) è la stessa di 570 (12 -> 3).
• Non garantisce la correttezza, ma solo la probabile correttezza: Potrebbe esserci un errore che la prova del nove non rileva, eppure l'operazione sembra corretta.

Esempio di errore non rilevato:

Supponiamo di aver calcolato 12 x 34 = 408, ma per errore scriviamo 12 x 34 = 480. Vediamo cosa succede con la prova del nove:

• 12: 1 + 2 = 3
• 34: 3 + 4 = 7
• 408: 4 + 0 + 8 = 12 -> 1 + 2 = 3
• 480: 4 + 8 + 0 = 12 -> 1 + 2 = 3

Moltiplicando i resti dei fattori: 3 x 7 = 21 -> 2 + 1 = 3. Questo corrisponde al resto di entrambi i risultati (sia quello corretto che quello errato). La prova del nove non rileva l'errore.

Consigli e Trucchi

• Semplifica il calcolo: Quando sommi le cifre, puoi ignorare i 9, perché non influenzano il resto modulo 9. Ad esempio, in 918, puoi ignorare il 9 e sommare solo 1 + 8 = 9, che dà resto 0.
• Usa la prova del nove in combinazione con altre tecniche: Per una maggiore sicurezza, combina la prova del nove con una stima approssimativa del risultato. Ad esempio, se stai moltiplicando 123 x 45, puoi stimare che il risultato sarà circa 100 x 50 = 5000. Questo ti aiuterà a individuare errori grossolani.
• Fai pratica: Più ti eserciti, più velocemente e accuratamente sarai in grado di applicare la prova del nove.

Conclusione

La prova del nove è uno strumento semplice e potente per verificare la correttezza dei calcoli aritmetici. Pur non essendo infallibile, offre una rapida e utile conferma della correttezza, soprattutto per gli errori più comuni. Imparare e utilizzare questa tecnica ti permetterà di avere maggiore fiducia nei tuoi calcoli e di evitare errori costosi. Quindi, la prossima volta che farai un calcolo, non dimenticare di applicare la prova del nove: potrebbe salvarti da brutte sorprese!