La Materia Con Seni E Coseni

L'universo che ci circonda, dalla più piccola particella subatomica alle vaste galassie, è governato da leggi fisiche che possono essere descritte matematicamente. Tra gli strumenti più potenti e versatili a nostra disposizione per comprendere e modellare questi fenomeni, troviamo le funzioni seno e coseno. Queste funzioni trigonometriche, apparentemente semplici, si rivelano pilastri fondamentali in una vasta gamma di discipline scientifiche e ingegneristiche, consentendoci di analizzare e prevedere comportamenti complessi e apparentemente casuali. Questo articolo si propone di esplorare la materia attraverso la lente di seni e coseni, rivelando la loro onnipresenza e la loro importanza cruciale.

L'Essenza di Seni e Coseni: Oltre il Triangolo Rettangolo

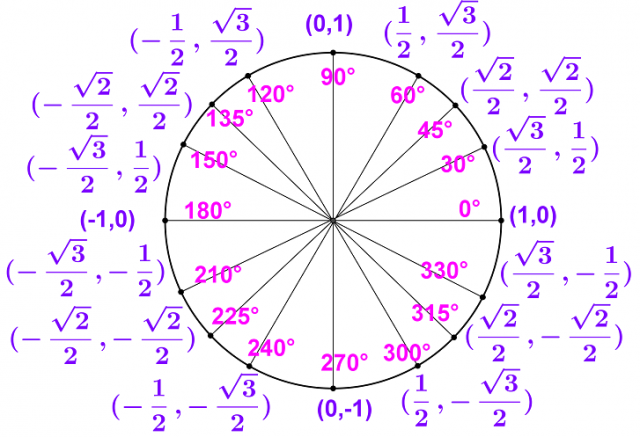
Comunemente introdotte nel contesto dei triangoli rettangoli, dove il seno di un angolo è definito come il rapporto tra il lato opposto e l'ipotenusa, e il coseno come il rapporto tra il lato adiacente e l'ipotenusa, le funzioni seno e coseno trascendono questa definizione limitata. La loro vera potenza emerge quando le consideriamo come funzioni periodiche. Questo significa che il loro valore si ripete regolarmente su un intervallo definito. Immaginiamo un punto che si muove attorno a un cerchio unitario (un cerchio con raggio 1). La coordinata x di questo punto rappresenta il coseno dell'angolo formato tra la linea che collega il punto all'origine e l'asse orizzontale, mentre la coordinata y rappresenta il seno dello stesso angolo.

Questa rappresentazione circolare rivela la natura ondulatoria di seni e coseni. Il grafico di queste funzioni è una sinusoide, una curva liscia e oscillante che si ripete all'infinito. Le caratteristiche principali di una sinusoide sono l'ampiezza (la distanza massima dalla linea centrale), il periodo (la lunghezza di un ciclo completo) e la fase (che determina la posizione orizzontale della curva).

Onde: La Manifestazione Fisica di Seni e Coseni

Uno degli ambiti in cui le funzioni seno e coseno trovano la loro applicazione più naturale è lo studio delle onde. Che si tratti di onde sonore, onde luminose, onde elettromagnetiche o onde sull'acqua, tutte possono essere descritte matematicamente utilizzando combinazioni di seni e coseni. La forma d'onda di un suono puro, ad esempio, è una sinusoide. L'ampiezza della sinusoide corrisponde al volume del suono, mentre la frequenza (l'inverso del periodo) corrisponde all'altezza del suono.

Le onde luminose, anch'esse descritte da funzioni sinusoidali, determinano il colore che percepiamo. Diverse frequenze corrispondono a diversi colori nello spettro visibile. La luce bianca, ad esempio, è una combinazione di onde luminose di diverse frequenze.

Anche le onde elettromagnetiche, che comprendono onde radio, microonde, raggi infrarossi, raggi ultravioletti, raggi X e raggi gamma, sono descritte da funzioni sinusoidali. La loro frequenza determina il tipo di onda elettromagnetica e le sue proprietà.

Analisi di Fourier: Decomporre la Complessità

Uno strumento matematico incredibilmente potente che sfrutta la natura periodica di seni e coseni è l'Analisi di Fourier. Questa tecnica ci permette di decomporre un segnale complesso, come un suono o un'immagine, in una somma di sinusoidi di diverse frequenze, ampiezze e fasi. In altre parole, possiamo considerare qualsiasi segnale come una sovrapposizione di onde semplici.

L'Analisi di Fourier ha applicazioni innumerevoli. Viene utilizzata in:

• Elaborazione del segnale audio: per equalizzare il suono, rimuovere il rumore e comprimere i file audio (come gli MP3).
• Elaborazione delle immagini: per migliorare la qualità delle immagini, rimuovere il rumore e comprimere i file immagine (come i JPEG).
• Telecomunicazioni: per modulare e demodulare i segnali radio e televisivi.
• Medicina: per analizzare segnali biologici come l'elettrocardiogramma (ECG) e l'elettroencefalogramma (EEG).
• Sismologia: per analizzare le onde sismiche e studiare la struttura interna della Terra.

Un esempio concreto è rappresentato dagli equalizzatori audio. Questi dispositivi utilizzano l'Analisi di Fourier per identificare le diverse frequenze presenti in un segnale audio e permettono all'utente di aumentare o diminuire l'ampiezza di specifiche frequenze, modificando così il timbro del suono.

Fenomeni Oscillatori: Dal Pendolo all'Elettronica

Molti fenomeni naturali e artificiali presentano un comportamento oscillatorio, ovvero un movimento che si ripete periodicamente attorno a una posizione di equilibrio. Esempi classici includono il pendolo, la molla e i circuiti elettrici oscillanti. La descrizione matematica di questi fenomeni coinvolge inevitabilmente le funzioni seno e coseno.

Il pendolo semplice, ad esempio, ha un periodo di oscillazione che dipende dalla sua lunghezza e dall'accelerazione di gravità. La posizione del pendolo nel tempo può essere descritta da una funzione sinusoidale. Allo stesso modo, un oggetto attaccato a una molla oscillerà attorno alla sua posizione di equilibrio con una frequenza che dipende dalla massa dell'oggetto e dalla costante elastica della molla. Anche in questo caso, la posizione dell'oggetto nel tempo è descritta da una sinusoide.

Nei circuiti elettrici oscillanti, come i circuiti LC (induttore-condensatore), l'energia viene scambiata periodicamente tra l'induttore e il condensatore, generando una corrente oscillante. La corrente e la tensione nel circuito variano sinusoidalmente nel tempo. Questi circuiti sono fondamentali per la creazione di oscillatori, che sono componenti essenziali in molti dispositivi elettronici, come radio, televisori e computer.

Dati Reali: La Meteorologia e le Maree

Le funzioni seno e coseno non sono solo astrazioni matematiche, ma trovano applicazione pratica nell'analisi di dati reali. Ad esempio, le temperature medie giornaliere nel corso di un anno possono essere approssimate da una funzione sinusoidale. L'ampiezza della sinusoide rappresenta la differenza tra la temperatura media massima e la temperatura media minima, mentre il periodo è di un anno.

Un altro esempio è rappresentato dalle maree. L'altezza dell'acqua del mare varia periodicamente a causa dell'attrazione gravitazionale della Luna e del Sole. Questa variazione può essere modellata utilizzando una combinazione di funzioni sinusoidali di diverse frequenze, corrispondenti ai diversi cicli di marea (diurno, semidiurno, etc.). Le previsioni delle maree, cruciali per la navigazione e la gestione delle coste, si basano su modelli matematici che utilizzano seni e coseni.

Analizzando i dati storici delle maree, è possibile estrarre le componenti sinusoidali principali e utilizzarle per prevedere le maree future con un certo grado di accuratezza. Questi modelli tengono conto anche di altri fattori, come la forma della costa e la profondità del mare, che influenzano il comportamento delle maree.

Navigazione: dalla Stella Polare al GPS

Storicamente, la navigazione astronomica si basava sulla misurazione degli angoli tra le stelle e l'orizzonte. Queste misurazioni, combinate con la conoscenza della posizione delle stelle nel tempo, permettevano ai marinai di determinare la loro latitudine e longitudine. La trigonometria, e quindi le funzioni seno e coseno, erano strumenti essenziali per effettuare questi calcoli.

Anche i moderni sistemi di navigazione satellitare, come il GPS, si basano su principi trigonometrici. Il GPS utilizza segnali provenienti da una rete di satelliti per determinare la posizione di un ricevitore sulla Terra. Il ricevitore calcola la sua distanza da almeno quattro satelliti, misurando il tempo impiegato dai segnali per raggiungere il ricevitore. Utilizzando la trilaterazione, un processo geometrico che coinvolge il calcolo di distanze e angoli, il ricevitore determina la sua posizione con grande precisione. Le funzioni seno e coseno sono fondamentali per effettuare i calcoli trigonometrici necessari per la trilaterazione.

Conclusione: Un Linguaggio Universale

Le funzioni seno e coseno, spesso percepite come argomenti astratti della matematica, si rivelano essere strumenti potenti e versatili per comprendere e modellare il mondo che ci circonda. Dalla fisica alla musica, dall'ingegneria alla medicina, dalla meteorologia alla navigazione, le loro applicazioni sono innumerevoli e pervasive. La loro natura periodica le rende particolarmente adatte per lo studio dei fenomeni oscillatori e ondulatori, che sono ubiquitari in natura.

Comprendere le proprietà e le applicazioni di seni e coseni è fondamentale per chiunque voglia approfondire la propria conoscenza della scienza e della tecnologia. Vi invitiamo ad esplorare ulteriormente questo affascinante campo, sperimentando con simulazioni, analizzando dati reali e applicando i concetti appresi a problemi concreti. La padronanza di questi strumenti matematici aprirà nuove prospettive e vi permetterà di interpretare il mondo con occhi diversi. Imparare ad usare seni e coseni, significa imparare un linguaggio universale, un linguaggio che descrive le fondamenta dell'universo.