Interferenza Costruttiva E Distruttiva Esercizi Svolti

Capita a volte di sentire un suono più forte del previsto, magari quando due altoparlanti suonano la stessa nota. Oppure, al contrario, un suono quasi sparire. Questo è il risultato dell'interferenza, un fenomeno ondulatorio fondamentale che si manifesta quando due o più onde si sovrappongono. In questo articolo, esploreremo l'interferenza costruttiva e distruttiva, analizzando esempi pratici ed esercizi svolti per comprenderne a fondo i meccanismi. Affronteremo il tema senza perdersi in tecnicismi eccessivi, cercando di rendere il concetto accessibile a tutti.

Cos'è l'Interferenza? Un'introduzione

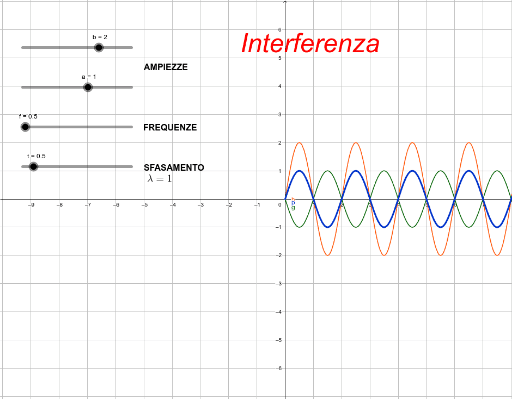
Immagina di lanciare due sassi in uno stagno. Vedrai formarsi delle onde concentriche che si propagano. Dove queste onde si incontrano, succede qualcosa di interessante: in alcuni punti l'acqua si alza più del normale, in altri si abbassa. Questo è un esempio di interferenza. In termini più formali, l'interferenza è la sovrapposizione di due o più onde, che si traduce in un'onda risultante la cui ampiezza è la somma algebrica delle ampiezze delle onde originali.

Interferenza Costruttiva: Quando le Onde Si Sommano

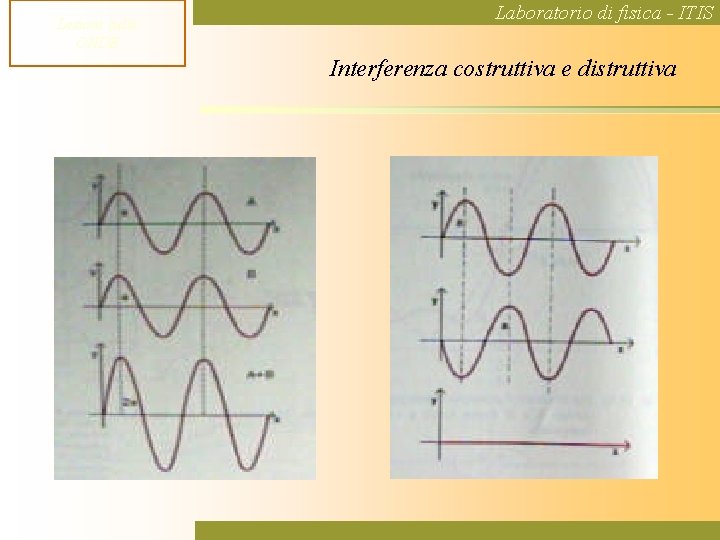
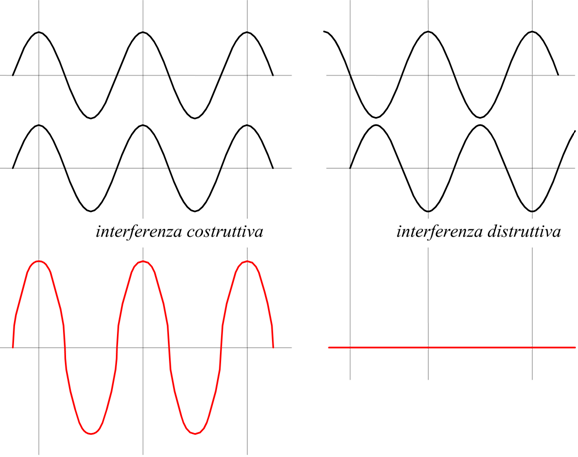
L'interferenza costruttiva si verifica quando le creste di due onde si sovrappongono, oppure quando i ventri (i punti più bassi) di due onde si sovrappongono. In questo caso, le ampiezze delle onde si sommano, creando un'onda risultante con un'ampiezza maggiore. Il risultato è un'onda più intensa.

Condizione: Le onde devono essere in fase, cioè le creste devono coincidere con le creste e i ventri con i ventri. Questo implica una differenza di percorso uguale a un numero intero di lunghezze d'onda (0λ, 1λ, 2λ, 3λ, etc.).
Esempio: Due altoparlanti che emettono lo stesso suono in fase creano un suono più forte in determinati punti.
Formula: Δx = nλ, dove Δx è la differenza di percorso, n è un numero intero (0, 1, 2, ...) e λ è la lunghezza d'onda.

Interferenza Distruttiva: Quando le Onde Si Annullano

L'interferenza distruttiva si verifica quando la cresta di un'onda si sovrappone al ventre di un'altra onda. In questo caso, le ampiezze delle onde si sottraggono, creando un'onda risultante con un'ampiezza minore. Se le ampiezze delle onde sono uguali, si può avere un'annullamento completo.

Condizione: Le onde devono essere in opposizione di fase, cioè le creste di una onda devono coincidere con i ventri dell'altra. Questo implica una differenza di percorso uguale a un numero semi-intero di lunghezze d'onda (0.5λ, 1.5λ, 2.5λ, etc.).
Esempio: Cancellazione del rumore nelle cuffie: il dispositivo genera un'onda sonora che è l'opposto di quella ambientale, causando interferenza distruttiva e riducendo il rumore percepito.
Formula: Δx = (n + 1/2)λ, dove Δx è la differenza di percorso, n è un numero intero (0, 1, 2, ...) e λ è la lunghezza d'onda.

Esercizi Svolti: Mettiamo in Pratica la Teoria

Per consolidare la comprensione dei concetti, affrontiamo alcuni esercizi pratici.

Esercizio 1: Due Sorgenti Sonore

Due altoparlanti identici emettono un suono con una lunghezza d'onda di 0.5 metri. Un ascoltatore si trova a 2 metri dal primo altoparlante e a 2.75 metri dal secondo. Si verifica interferenza costruttiva o distruttiva nel punto in cui si trova l'ascoltatore?

Soluzione:

Calcola la differenza di percorso (Δx): Δx = 2.75 m - 2 m = 0.75 m
Verifica se Δx è un multiplo intero o semi-intero della lunghezza d'onda (λ): Dividiamo Δx per λ: 0.75 m / 0.5 m = 1.5.
Conclusione: Poiché 1.5 è un numero semi-intero, si verifica interferenza distruttiva.

Esercizio 2: Esperimento di Young (Doppia Fenditura)

In un esperimento di Young, la distanza tra le due fenditure è di 0.1 mm e la distanza tra le fenditure e lo schermo è di 1 metro. Se la luce utilizzata ha una lunghezza d'onda di 500 nm (nanometri), qual è la distanza tra la frangia centrale luminosa (massimo centrale) e la prima frangia luminosa successiva (primo massimo)?

Soluzione:

La formula per la posizione dei massimi in un esperimento di Young è: y = (nλL) / d, dove:

y è la distanza dal massimo centrale
n è l'ordine del massimo (0 per il massimo centrale, 1 per il primo massimo, etc.)
λ è la lunghezza d'onda
L è la distanza tra le fenditure e lo schermo
d è la distanza tra le fenditure

Calcola la posizione del massimo centrale (n=0): y₀ = (0 * 500 nm * 1 m) / 0.1 mm = 0 m
Calcola la posizione del primo massimo (n=1): y₁ = (1 * 500 * 10^-9 m * 1 m) / (0.1 * 10^-3 m) = 0.005 m = 5 mm
Calcola la distanza tra i due massimi: Δy = y₁ - y₀ = 5 mm - 0 mm = 5 mm
Conclusione: La distanza tra la frangia centrale luminosa e la prima frangia luminosa successiva è di 5 mm.

Esercizio 3: Interferenza in una Pellicola Sottile

Una pellicola sottile di olio (indice di rifrazione n = 1.42) galleggia sull'acqua (indice di rifrazione n = 1.33). La luce bianca incide normalmente sulla pellicola. Quale spessore minimo deve avere la pellicola affinché la luce con una lunghezza d'onda di 560 nm sia riflessa intensamente (interferenza costruttiva)? Considera il fatto che la luce subisce un'inversione di fase quando si riflette da un materiale con un indice di rifrazione maggiore.

Soluzione:

In questo caso, la luce che si riflette sulla superficie superiore dell'olio subisce un'inversione di fase (perché l'indice di rifrazione dell'olio è maggiore di quello dell'aria). La luce che si riflette sulla superficie inferiore dell'olio *non* subisce un'inversione di fase (perché l'indice di rifrazione dell'olio è maggiore di quello dell'acqua). Per avere interferenza costruttiva, la differenza di percorso (2t, dove t è lo spessore della pellicola) deve essere uguale a un numero semi-intero di lunghezze d'onda *nella pellicola*, più l'inversione di fase. La lunghezza d'onda nella pellicola è λ/n, dove λ è la lunghezza d'onda nel vuoto.

La condizione per interferenza costruttiva è quindi: 2t = (m + 1/2) (λ/n), dove m è un numero intero (0, 1, 2, ...).

Per trovare lo spessore minimo, usiamo m = 0: 2t = (1/2) (λ/n)

Risolviamo per t: t = (λ) / (4n) = (560 nm) / (4 * 1.42) = 98.59 nm

Conclusione: Lo spessore minimo della pellicola affinché la luce con una lunghezza d'onda di 560 nm sia riflessa intensamente è di circa 98.59 nm.

Applicazioni Pratiche dell'Interferenza

L'interferenza non è solo un concetto teorico. Trova applicazioni concrete in diversi campi:

Cancellazione del rumore: Come accennato, le cuffie a cancellazione del rumore utilizzano l'interferenza distruttiva per ridurre il rumore ambientale.
Olografia: L'olografia si basa sull'interferenza per registrare e ricostruire immagini tridimensionali.
Rivestimenti antiriflesso: Le lenti degli occhiali e le fotocamere sono spesso rivestite con materiali sottili che sfruttano l'interferenza distruttiva per ridurre i riflessi.
Interferometri: Gli interferometri sono strumenti di precisione che utilizzano l'interferenza per misurare distanze, spessori e variazioni di indice di rifrazione con elevata accuratezza.

Controversie e Approfondimenti

Sebbene i principi dell'interferenza siano ben consolidati, la comprensione completa di fenomeni complessi come l'interferenza quantistica rimane un campo attivo di ricerca. Alcuni potrebbero sostenere che la modellizzazione classica dell'interferenza è sufficiente per la maggior parte delle applicazioni pratiche, mentre altri sottolineano l'importanza di considerare gli effetti quantistici per una descrizione più accurata a livello fondamentale. In ogni caso, l'interferenza rappresenta un concetto chiave per comprendere il comportamento ondulatorio della luce e di altre onde.

In Sintesi

L'interferenza, sia costruttiva che distruttiva, è un fenomeno ondulatorio che influenza profondamente il modo in cui percepiamo e interagiamo con il mondo che ci circonda. Comprendere i suoi principi è fondamentale per diverse discipline, dalla fisica all'ingegneria. Attraverso esercizi pratici e applicazioni reali, abbiamo visto come l'interferenza non sia solo una teoria, ma una forza tangibile con impatti concreti.

Ora, rifletti su questo: quali altri esempi di interferenza riesci a individuare nella tua vita quotidiana? Come potrebbe essere sfruttata ulteriormente per migliorare la tecnologia o risolvere problemi specifici?