Il Rombo Ha I Lati Uguali

L'affermazione "Il rombo ha i lati uguali" è una verità fondamentale della geometria euclidea. Ma cosa significa veramente? E perché è importante? In questo articolo, esploreremo a fondo questa proprietà caratteristica del rombo, analizzando le sue implicazioni, le sue relazioni con altre figure geometriche, e le sue applicazioni nel mondo reale.

Le Proprietà Fondamentali del Rombo

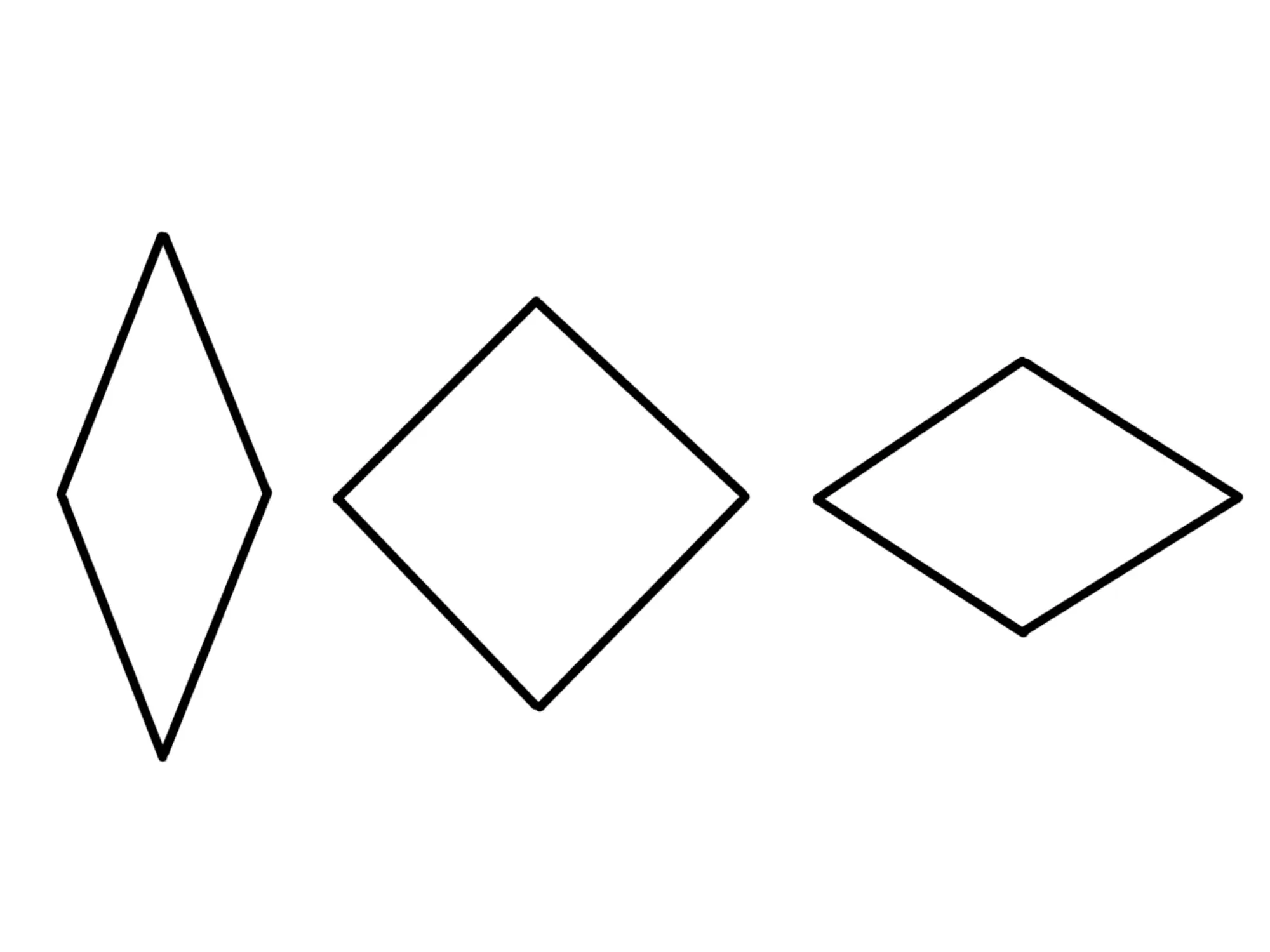
Un rombo è un quadrilatero speciale che possiede alcune proprietà distintive. La più importante, come già detto, è che tutti i suoi quattro lati sono congruenti, ovvero hanno la stessa lunghezza. Questa caratteristica lo distingue da altri quadrilateri, come il rettangolo o il trapezio.

Lati Congruenti: La Chiave di Volta

La congruenza dei lati è la definizione stessa di rombo. Se un quadrilatero ha tutti i lati uguali, allora è un rombo. Non ci sono eccezioni. Questa proprietà è fondamentale per derivare altre caratteristiche del rombo.

Angoli Opposti Uguali e Angoli Adiacenti Supplementari

Un'altra proprietà importante del rombo è che i suoi angoli opposti sono congruenti. Questo significa che gli angoli che non condividono un lato sono uguali tra loro. Inoltre, gli angoli adiacenti (quelli che condividono un lato) sono supplementari, ovvero la loro somma è 180 gradi.

Diagonali Perpendicolari e Bisettrici

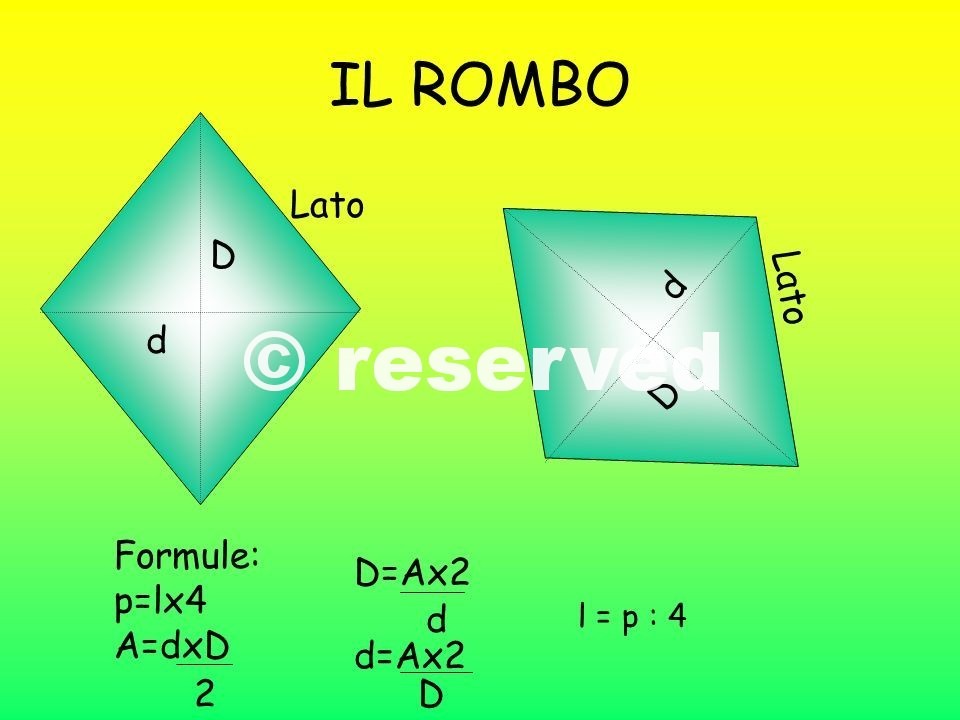
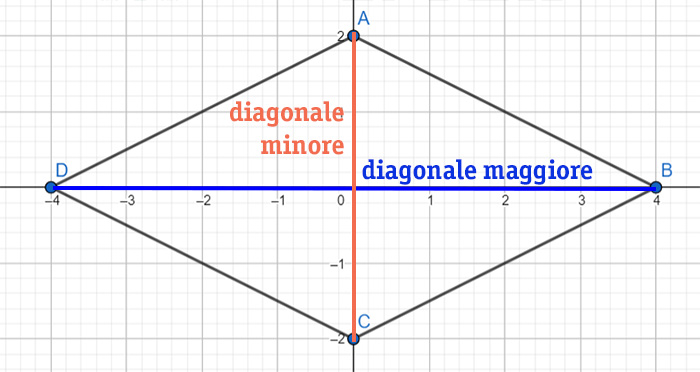
Le diagonali di un rombo (i segmenti che congiungono i vertici opposti) si intersecano perpendicolarmente. Questo significa che formano quattro angoli retti nel punto in cui si incontrano. Inoltre, le diagonali di un rombo sono anche bisettrici degli angoli ai vertici. Questo significa che ogni diagonale divide l'angolo al vertice in due angoli congruenti.

Rombo vs. Quadrato: Una Sottile Differenza

Il quadrato è un caso speciale di rombo. Un quadrato è un rombo che ha anche tutti gli angoli retti (90 gradi). In altre parole, un quadrato soddisfa sia la definizione di rombo (lati uguali) che quella di rettangolo (angoli retti). Pertanto, ogni quadrato è un rombo, ma non tutti i rombi sono quadrati.

La differenza cruciale sta negli angoli. Un rombo può avere angoli diversi da 90 gradi, mentre un quadrato deve necessariamente averli tutti retti.

Dimostrazione Geometrica della Congruenza dei Lati

La congruenza dei lati può essere dimostrata formalmente utilizzando i principi della geometria euclidea. Una dimostrazione semplice si basa sulla costruzione di triangoli congruenti all'interno del rombo. Tracciando le diagonali, si formano quattro triangoli rettangoli congruenti (per il criterio lato-angolo-lato, o LAL), il che implica che tutti i lati del rombo sono uguali.

Questa dimostrazione rigorosa consolida la validità dell'affermazione "Il rombo ha i lati uguali" all'interno del sistema assiomatico della geometria.

Applicazioni Pratiche del Rombo

Il rombo, pur essendo una figura geometrica astratta, trova numerose applicazioni nel mondo reale. Le sue proprietà uniche lo rendono utile in diversi campi, dall'architettura al design, fino all'ingegneria.

Architettura e Design

Le forme romboidali sono spesso utilizzate in architettura per creare disegni e pattern decorativi. I pavimenti con piastrelle a forma di rombo, ad esempio, offrono un aspetto elegante e dinamico. Anche nel design di mobili e oggetti, il rombo può essere impiegato per aggiungere un tocco di originalità e modernità.

Pensate alle finestre a forma di rombo che si trovano spesso negli edifici storici, oppure ai pattern geometrici romboidali che decorano tessuti e carta da parati. La versatilità del rombo lo rende un elemento di design molto apprezzato.

Ingegneria e Strutture

In ingegneria, la forma del rombo può essere sfruttata per la costruzione di strutture leggere e resistenti. Ad esempio, le strutture reticolari romboidali offrono un'ottima rigidità e possono sopportare carichi elevati. Queste strutture sono utilizzate in ponti, torri e altre costruzioni complesse.

La geometria del rombo, con le sue diagonali perpendicolari e gli angoli specifici, permette di distribuire le forze in modo efficiente, rendendo le strutture più stabili e resistenti.

Cristallografia

Nel campo della cristallografia, molti cristalli presentano forme romboidali. La forma esterna di un cristallo riflette la sua struttura interna, e la presenza di facce romboidali indica una specifica disposizione degli atomi all'interno del cristallo. Lo studio di queste forme aiuta a comprendere le proprietà dei materiali.

L'analisi delle forme cristalline, inclusi i rombi, è fondamentale per la caratterizzazione dei materiali e per lo sviluppo di nuove tecnologie.

Esempi Concreti

* Segnali stradali: Alcuni segnali stradali, come quelli di pericolo, hanno forma romboidale per attirare l'attenzione degli automobilisti.

* Aquiloni: La forma a rombo è molto comune negli aquiloni, in quanto offre un buon equilibrio e stabilità durante il volo.

* Logo aziendale: Molte aziende utilizzano il rombo nel loro logo per comunicare solidità, stabilità e innovazione.

Conclusione

L'affermazione "Il rombo ha i lati uguali" è molto più di una semplice definizione geometrica. È la base per comprendere le proprietà, le applicazioni e le relazioni di questa figura con altre forme geometriche. La sua presenza nel mondo reale, dall'architettura all'ingegneria, dimostra la sua importanza pratica e la sua versatilità.

Invitiamo quindi il lettore a osservare attentamente il mondo che lo circonda, alla ricerca di rombi nascosti in oggetti di uso quotidiano, strutture architettoniche e disegni decorativi. La geometria è ovunque, e comprenderla significa apprezzare la bellezza e l'ordine che governano il nostro universo.

Speriamo che questo articolo abbia contribuito a chiarire le proprietà del rombo e a stimolare la curiosità del lettore verso la geometria. Approfondire la conoscenza della geometria è un investimento prezioso per sviluppare il pensiero critico e la capacità di risolvere problemi.