Il Punto Di Intersezione Delle Altezze Di Un Triangolo

La geometria euclidea, con la sua eleganza e precisione, ci offre una miriade di concetti affascinanti. Uno di questi è l'ortocentro di un triangolo, un punto cruciale determinato dall'intersezione delle sue altezze. Comprendere cos'è l'ortocentro e come si calcola è fondamentale per apprezzare appieno le proprietà dei triangoli e le loro applicazioni in vari campi.

Definizione e Concetti Fondamentali

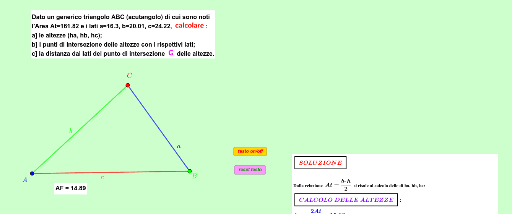
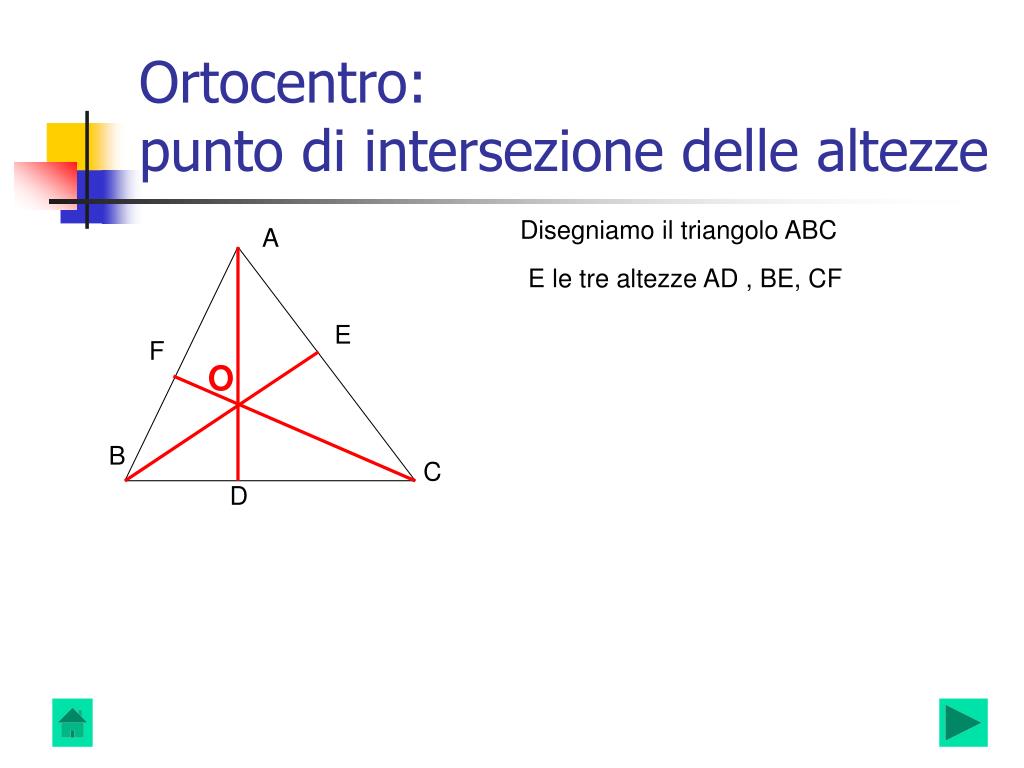
L'altezza di un triangolo è un segmento di retta che parte da un vertice e cade perpendicolarmente sul lato opposto, o sul prolungamento di esso. Ogni triangolo ha quindi tre altezze, una per ciascun vertice. L'ortocentro è semplicemente il punto in cui queste tre altezze si incontrano. Questo punto di intersezione possiede proprietà uniche e la sua posizione varia a seconda del tipo di triangolo.

Triangoli Acutangoli, Rettangoli e Ottusangoli

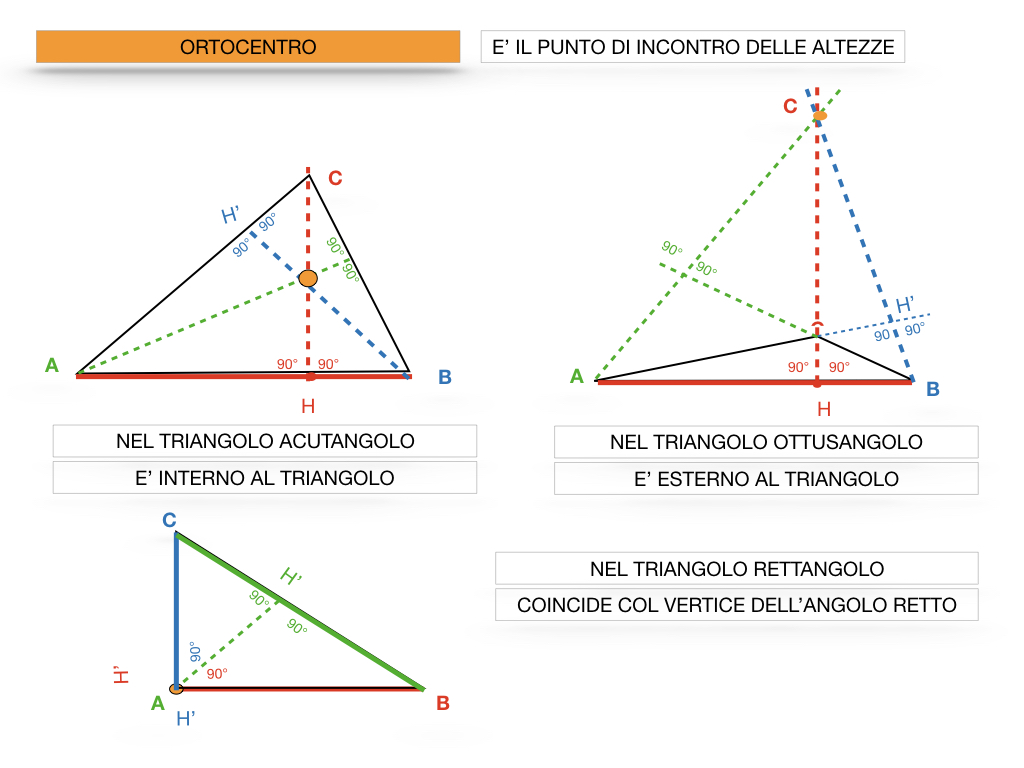
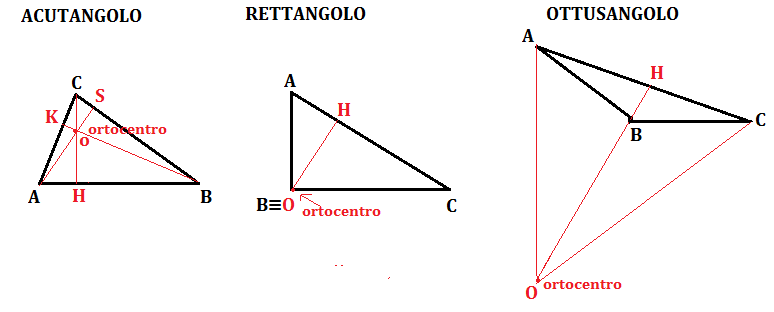
La posizione dell'ortocentro varia in base al tipo di triangolo:

• Triangolo Acutangolo: In un triangolo acutangolo, dove tutti gli angoli sono minori di 90 gradi, l'ortocentro si trova all'interno del triangolo.
• Triangolo Rettangolo: In un triangolo rettangolo, dove uno degli angoli è esattamente 90 gradi, l'ortocentro coincide con il vertice dell'angolo retto. Questo è un caso particolare e facilmente identificabile.
• Triangolo Ottusangolo: In un triangolo ottusangolo, dove uno degli angoli è maggiore di 90 gradi, l'ortocentro si trova all'esterno del triangolo. Questo perché le altezze relative agli angoli acuti si intersecano al di fuori del triangolo.

Comprendere queste distinzioni è cruciale per visualizzare e interpretare correttamente le proprietà dell'ortocentro.

Come Trovare l'Ortocentro: Metodi e Calcoli

Esistono diversi metodi per determinare la posizione dell'ortocentro di un triangolo. Alcuni sono geometrici, altri analitici.

Metodo Geometrico

Il metodo geometrico è concettualmente semplice: si tracciano le tre altezze del triangolo. Il punto in cui si intersecano è l'ortocentro. Questo metodo è utile per visualizzare l'ortocentro e comprenderne la relazione con le altezze, ma può essere impreciso a causa degli errori di disegno.

Metodo Analitico

Il metodo analitico, basato sulla geometria analitica, offre maggiore precisione. Richiede la conoscenza delle coordinate dei vertici del triangolo. Ecco i passaggi principali:

1. Calcolare le pendenze dei lati: Dati i vertici A(x₁, y₁), B(x₂, y₂) e C(x₃, y₃), si calcolano le pendenze dei lati AB, BC e CA utilizzando la formula: m = (y₂ - y₁) / (x₂ - x₁).
2. Calcolare le pendenze delle altezze: La pendenza di un'altezza è l'inverso negativo della pendenza del lato a cui è perpendicolare. Ad esempio, l'altezza relativa al lato BC ha pendenza -1/m(BC).
3. Scrivere le equazioni delle altezze: Utilizzando la forma punto-pendenza dell'equazione di una retta (y - y₁ = m(x - x₁)), si scrivono le equazioni di due altezze. Ad esempio, l'equazione dell'altezza relativa al lato BC e passante per A è: y - y₁ = (-1/m(BC))(x - x₁).
4. Risolvere il sistema di equazioni: Si risolve il sistema formato dalle equazioni delle due altezze. La soluzione (x, y) rappresenta le coordinate dell'ortocentro.

Questo metodo richiede una buona conoscenza dell'algebra e della geometria analitica, ma fornisce risultati precisi.

Esempio Pratico

Consideriamo un triangolo con vertici A(1, 2), B(4, 6) e C(7, 1). Seguiamo i passaggi del metodo analitico:

1. Pendenze dei lati:
   • m(AB) = (6 - 2) / (4 - 1) = 4/3
   • m(BC) = (1 - 6) / (7 - 4) = -5/3
   • m(CA) = (2 - 1) / (1 - 7) = -1/6
2. Pendenze delle altezze:
   • Altezza relativa a BC: 3/5
   • Altezza relativa a CA: 6
3. Equazioni delle altezze:
   • Altezza relativa a BC passante per A: y - 2 = (3/5)(x - 1) => y = (3/5)x + 7/5
   • Altezza relativa a CA passante per B: y - 6 = 6(x - 4) => y = 6x - 18
4. Risoluzione del sistema:
   • (3/5)x + 7/5 = 6x - 18
   • (3/5)x - 6x = -18 - 7/5
   • (-27/5)x = -97/5
   • x = 97/27 ≈ 3.59
   • y = 6(97/27) - 18 = 582/27 - 486/27 = 96/27 = 32/9 ≈ 3.56

Quindi, l'ortocentro del triangolo ABC è approssimativamente (3.59, 3.56).

Proprietà Importanti dell'Ortocentro

L'ortocentro non è solo un punto di intersezione; possiede diverse proprietà interessanti:

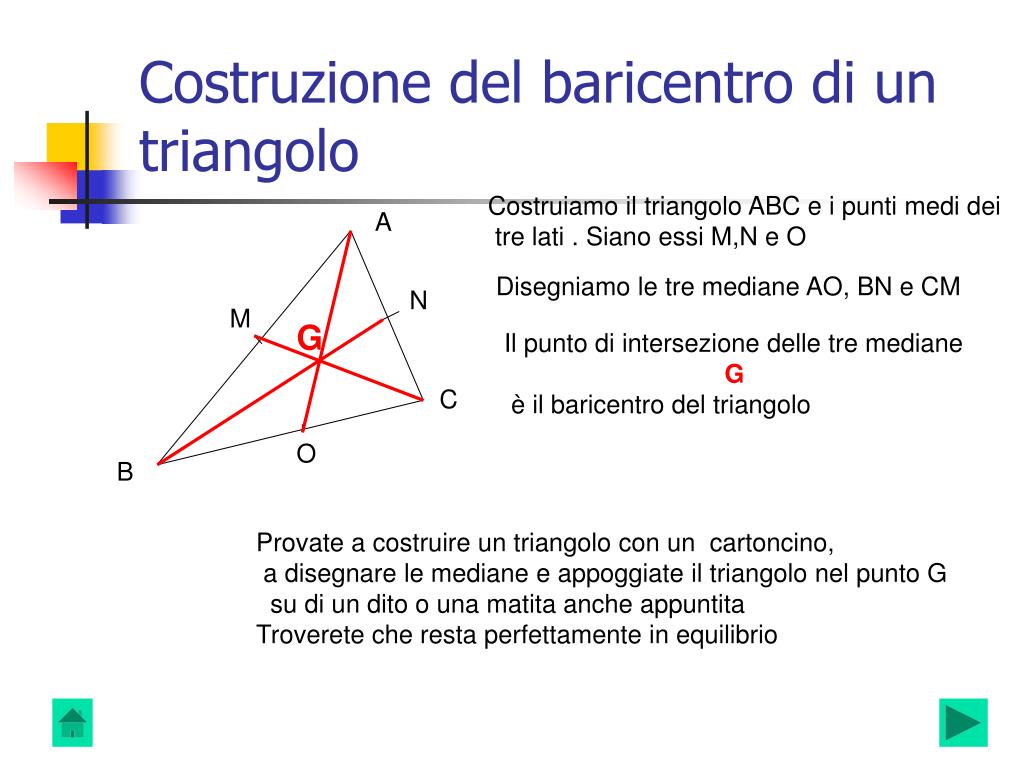
• Relazione con il Circocentro e il Baricentro: L'ortocentro, il circocentro (centro della circonferenza circoscritta) e il baricentro (centro di massa) di un triangolo sono collineari. Questa linea è chiamata retta di Eulero. Questa proprietà stabilisce una connessione profonda tra diversi punti notevoli del triangolo.
• L'Ortocentro come Vertice: Se si considerano le altezze di un triangolo come lati di un nuovo triangolo, l'ortocentro del triangolo originale diventa un vertice di questo nuovo triangolo.
• Simmetria: L'ortocentro rivela alcune simmetrie all'interno del triangolo e nelle sue relazioni con le altezze.

Applicazioni Pratiche

Sebbene l'ortocentro possa sembrare un concetto puramente teorico, trova applicazioni in diversi campi:

Ingegneria e Architettura

In ingegneria strutturale, la comprensione delle proprietà dei triangoli e dei loro punti notevoli, inclusa l'ortocentro, è essenziale per progettare strutture stabili e resistenti. Ad esempio, nella costruzione di ponti e torri, i triangoli vengono utilizzati per distribuire il carico in modo uniforme. La posizione precisa dell'ortocentro può influenzare la stabilità e la distribuzione delle forze all'interno della struttura.

Grafica Computerizzata e Animazione

Nella grafica computerizzata, i triangoli sono spesso utilizzati per rappresentare superfici tridimensionali. La conoscenza dell'ortocentro può essere utile per calcolare le normali alle superfici e per implementare algoritmi di rendering e illuminazione.

Geodesia e Cartografia

In geodesia e cartografia, i triangoli geodetici sono utilizzati per misurare e mappare la superficie terrestre. La posizione precisa dei vertici e dei punti notevoli, come l'ortocentro, è fondamentale per garantire l'accuratezza delle misurazioni e delle mappe.

Astronomia

In astronomia, la triangolazione è utilizzata per determinare le distanze tra gli oggetti celesti. La conoscenza delle proprietà dei triangoli, incluso l'ortocentro, può essere utile per migliorare l'accuratezza delle misurazioni astronomiche.

Conclusioni

L'ortocentro di un triangolo è un punto notevole con proprietà affascinanti e applicazioni pratiche. Dalla sua definizione geometrica al suo calcolo analitico, dalla sua relazione con altri punti notevoli alle sue applicazioni in ingegneria, grafica computerizzata e altre discipline, l'ortocentro dimostra la potenza e l'eleganza della geometria euclidea. Comprendere questo concetto non solo arricchisce la nostra conoscenza della geometria, ma ci fornisce anche strumenti utili per risolvere problemi pratici in vari campi.

Esplora, sperimenta e approfondisci la tua conoscenza dei triangoli e dei loro punti notevoli. La bellezza della matematica risiede nella sua capacità di rivelare connessioni inaspettate e di fornire soluzioni eleganti ai problemi complessi.