Il Numero 0 è Pari O Dispari

La domanda se il numero zero sia pari o dispari suscita spesso curiosità e a volte anche dibattiti. A prima vista, potrebbe sembrare una questione puramente teorica, senza alcuna implicazione pratica. Tuttavia, capire la parità di zero è fondamentale per la coerenza di diverse aree della matematica e dell'informatica. Questo articolo esplorerà in dettaglio perché zero è considerato un numero pari, esaminando le definizioni, le dimostrazioni e le implicazioni che ne derivano.

Definizione di Numeri Pari e Dispari

Per comprendere la parità di zero, è essenziale definire cosa si intende per numero pari e dispari. Un numero è considerato pari se è un multiplo di 2, ovvero se può essere diviso per 2 senza lasciare resto. Matematicamente, un numero intero 'n' è pari se esiste un altro numero intero 'k' tale che n = 2k. Un numero è considerato dispari se, quando diviso per 2, lascia un resto di 1. In altre parole, un numero intero 'n' è dispari se esiste un numero intero 'k' tale che n = 2k + 1.

Applicazione della Definizione a Zero

Applichiamo ora queste definizioni a zero. Possiamo esprimere zero come un multiplo di 2? Sì. Zero può essere scritto come 0 = 2 * 0. Poiché esiste un numero intero (in questo caso, 0 stesso) che moltiplicato per 2 dà 0, allora zero soddisfa la definizione di un numero pari. Non lascia alcun resto quando diviso per 2, confermando ulteriormente la sua parità.

Argomentazioni a Favore della Parità di Zero

Oltre alla definizione, ci sono diverse argomentazioni che supportano la classificazione di zero come numero pari.

Coerenza con i Modelli Numerici

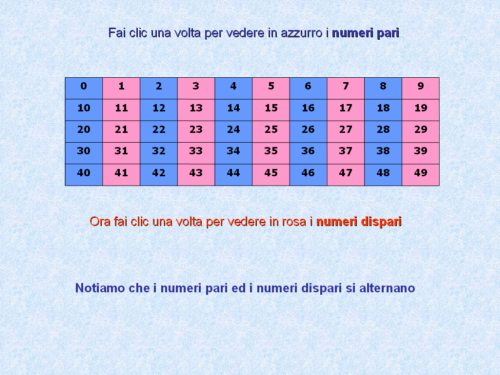
Consideriamo la successione di numeri interi: ..., -3, -2, -1, 0, 1, 2, 3, ... Notiamo che i numeri pari e dispari si alternano. Se zero fosse dispari, romperemmo questo schema. La sequenza diventerebbe: ..., dispari, pari, dispari, dispari, pari, dispari, ... Questo creerebbe un'incongruenza in un modello altrimenti ben definito.

Proprietà Algebriche

Le proprietà algebriche dei numeri pari e dispari forniscono ulteriori prove. Ad esempio:

• La somma di due numeri pari è pari: Se prendiamo due numeri pari qualsiasi, come 2 e 4, la loro somma (6) è anch'essa pari. Questo vale anche se uno dei numeri è zero: 2 + 0 = 2 (pari).
• La somma di due numeri dispari è pari: Ad esempio, 3 + 5 = 8 (pari). Se zero fosse dispari, la somma di un numero dispari e zero sarebbe pari, il che contraddirebbe la proprietà (dato che la somma dovrebbe essere dispari se zero fosse dispari).
• La somma di un numero pari e un numero dispari è dispari: Ad esempio, 2 + 3 = 5 (dispari). Questo rimane vero se uno dei numeri pari è zero: 0 + 3 = 3 (dispari).

Queste proprietà si mantengono coerenti solo se zero è considerato pari.

Test di Divisibilità per 2

Un numero è pari se è divisibile per 2. Zero è divisibile per 2, poiché 0 / 2 = 0, senza alcun resto. Questo è un altro modo per dimostrare che zero soddisfa la definizione di un numero pari.

Implicazioni e Applicazioni Pratiche

La parità di zero non è solo un concetto teorico; ha implicazioni pratiche in diverse aree, tra cui:

Informatica

In informatica, i test di parità sono usati per rilevare errori nella trasmissione dei dati. Un bit di parità è aggiunto a un gruppo di bit per rendere il numero totale di bit '1' pari o dispari, a seconda del tipo di test di parità (pari o dispari). La corretta identificazione di zero come numero pari è cruciale per il corretto funzionamento di questi test.

Matematica

In teoria dei numeri, la parità di zero è fondamentale per diverse dimostrazioni e teoremi. Ad esempio, il concetto di numeri pari e dispari è utilizzato in teoremi relativi alla divisibilità e alla fattorizzazione.

Algoritmi

Molti algoritmi utilizzano la parità di un numero come condizione per eseguire determinate operazioni. Se zero fosse erroneamente considerato dispari, questi algoritmi potrebbero comportarsi in modo inatteso o errato.

Esempi Concreti

Consideriamo alcuni esempi che dimostrano come la parità di zero influisce su diverse operazioni matematiche e informatiche:

• Calcolo Modulo: L'operatore modulo (%) restituisce il resto di una divisione. Se calcoliamo 5 % 2 otteniamo 1 (dispari). Se calcoliamo 4 % 2 otteniamo 0 (pari). Allo stesso modo, 0 % 2 restituisce 0, confermando che zero si comporta come un numero pari.
• Funzioni che dipendono dalla parità: Molti linguaggi di programmazione hanno funzioni che si comportano diversamente a seconda che un numero sia pari o dispari. Se zero fosse considerato dispari, queste funzioni produrrebbero risultati inattesi quando applicate a zero.
• Array e Indici: In molti linguaggi di programmazione, gli array iniziano con l'indice 0. La parità di questo indice iniziale influisce su come gli elementi dell'array vengono elaborati in determinati algoritmi.

Confutazione di Argomentazioni Contraddittorie

Occasionalmente, si può incontrare l'argomentazione che zero non è né pari né dispari. Questa affermazione deriva spesso da una comprensione incompleta della definizione di numeri pari e dispari. Come abbiamo dimostrato, zero soddisfa la definizione di numero pari e si comporta coerentemente con le proprietà algebriche associate ai numeri pari.

Un'altra possibile fonte di confusione è l'idea che zero rappresenta "nulla". Tuttavia, in matematica, zero è un numero ben definito con proprietà specifiche, e la sua classificazione come pari è essenziale per mantenere la coerenza del sistema numerico.

Conclusione

In definitiva, la risposta alla domanda "Il numero zero è pari o dispari?" è chiara e inequivocabile: zero è un numero pari. Questa conclusione è supportata dalla definizione di numeri pari, dalla coerenza con i modelli numerici, dalle proprietà algebriche e dalle applicazioni pratiche in matematica e informatica. Accettare la parità di zero è fondamentale per una comprensione completa e coerente del sistema numerico. Ignorare o contestare questa realtà porterebbe a incongruenze e potenziali errori in vari ambiti scientifici e tecnici.

Quindi, la prossima volta che ti imbatti in questa domanda, rispondi con sicurezza: zero è pari. Diffondi la conoscenza e aiuta a dissipare qualsiasi confusione residua su questo argomento fondamentale.