I Numeri Primi Fino A 100

Ti sei mai chiesto quali sono i mattoni fondamentali dei numeri? Forse hai sempre pensato ai numeri primi come a qualcosa di astratto, relegato alle lezioni di matematica del liceo. Ma la verità è che i numeri primi sono essenziali per comprendere la struttura stessa dei numeri e hanno applicazioni concrete nella vita di tutti i giorni, dalla crittografia che protegge le tue transazioni online alla composizione di algoritmi complessi.

Molti di noi ricordano vagamente di aver studiato i numeri primi, ma spesso la loro importanza e la loro applicabilità concreta sfuggono. Questo articolo è pensato per te, che magari ti sei dimenticato cosa sono i numeri primi, o che vuoi semplicemente riscoprirli sotto una luce nuova e più interessante. Ci concentreremo sui numeri primi fino a 100, esplorando cosa sono, come identificarli e perché sono così importanti. Non useremo gergo matematico inutilmente complicato, ma ci concentreremo su spiegazioni chiare e pratiche.

Cosa sono i Numeri Primi?

Un numero primo è un numero naturale maggiore di 1 che ha solamente due divisori: 1 e se stesso. In altre parole, un numero primo non può essere diviso esattamente per nessun altro numero, tranne 1 e il numero stesso. Questo significa che se provi a dividere un numero primo per qualsiasi altro numero (eccetto 1 e se stesso), otterrai sempre un resto.

Ad esempio, il numero 7 è un numero primo perché può essere diviso solo per 1 e per 7. Se provi a dividerlo per 2, 3, 4, 5 o 6, otterrai sempre un resto. Il numero 4, invece, non è un numero primo perché può essere diviso per 1, 2 e 4.

È importante sottolineare che il numero 1 non è considerato un numero primo. La definizione formale richiede che un numero primo abbia esattamente due divisori, mentre 1 ne ha solo uno (se stesso).

Come Identificare i Numeri Primi Fino A 100

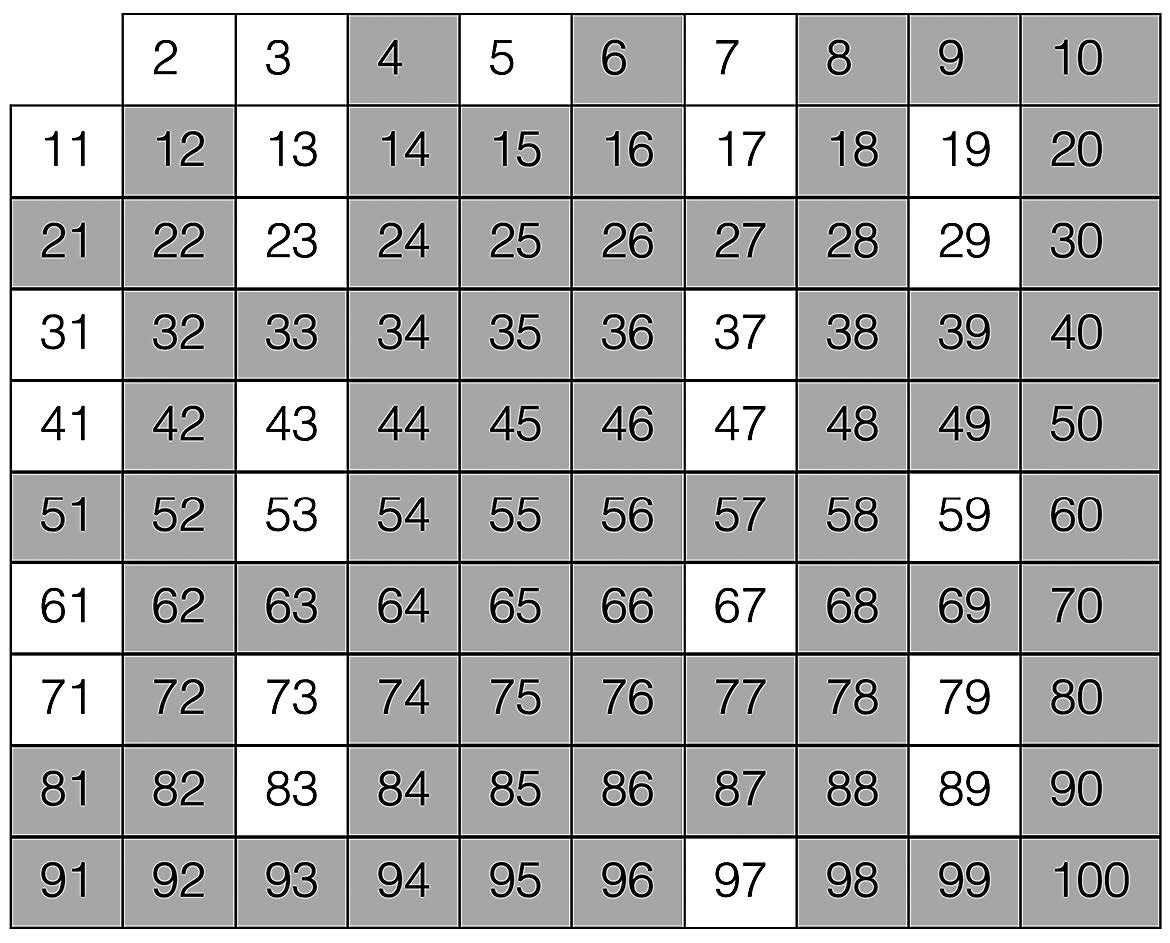
Esistono diversi metodi per identificare i numeri primi. Uno dei più antichi e semplici è il Crivello di Eratostene, un algoritmo che prende il nome dal matematico greco Eratostene di Cirene.

Il Crivello di Eratostene: Un Metodo Antico e Affidabile

Il Crivello di Eratostene è un metodo visivo e intuitivo per trovare i numeri primi entro un certo intervallo. Ecco come funziona:

1. Scrivi tutti i numeri naturali da 2 fino al numero massimo che ti interessa (in questo caso, 100).
2. Il primo numero della lista, 2, è un numero primo. Cerchialo.
3. Cancella tutti i multipli di 2 (4, 6, 8, 10, e così via) fino a 100.
4. Il numero successivo non cancellato nella lista è il numero primo successivo (in questo caso, 3). Cerchialo.
5. Cancella tutti i multipli di 3 (6, 9, 12, 15, e così via) fino a 100. Nota che alcuni numeri (come 6) saranno già stati cancellati.
6. Continua questo processo, cerchiando il prossimo numero non cancellato (che sarà sempre un numero primo) e cancellando tutti i suoi multipli.
7. Quando raggiungi un numero il cui quadrato è maggiore del numero massimo della tua lista (in questo caso, 100), tutti i numeri rimasti non cancellati sono numeri primi.

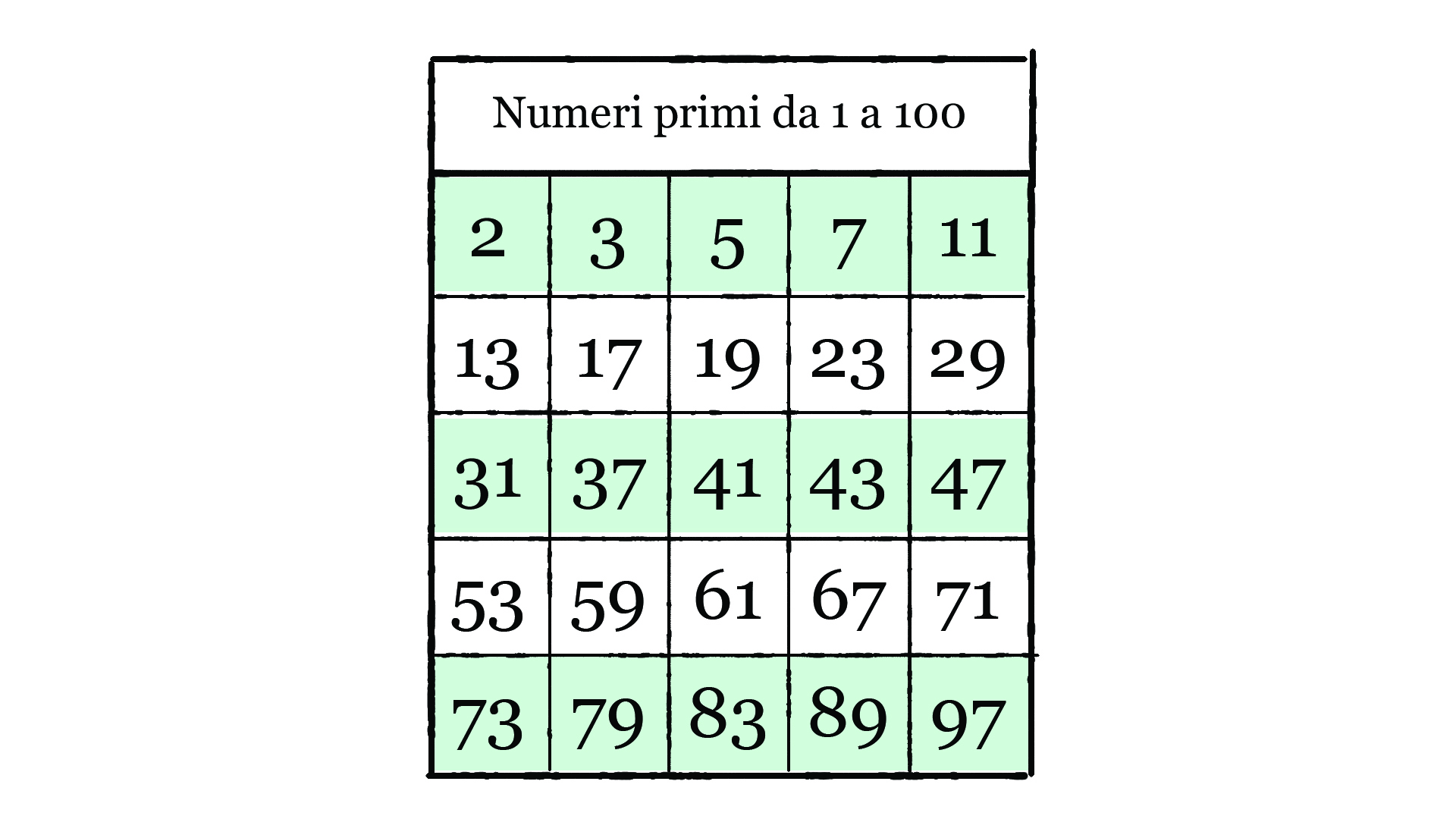
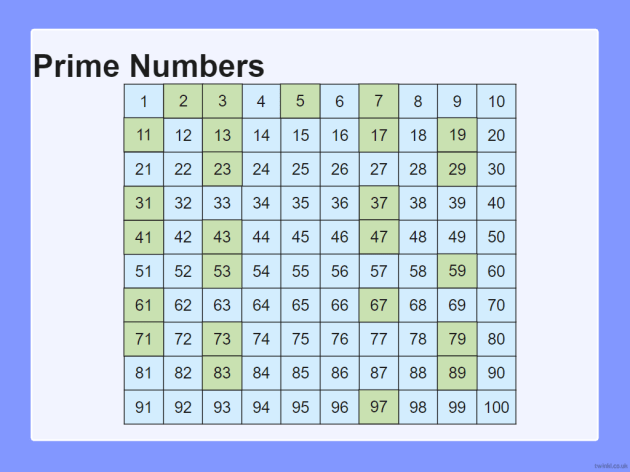
Seguendo questo metodo, troverai che i numeri primi fino a 100 sono:

2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47, 53, 59, 61, 67, 71, 73, 79, 83, 89, 97.

Un Approccio Più Moderno: La Divisione per Tentativi

Un altro metodo per identificare i numeri primi, anche se meno efficiente per intervalli ampi, è la divisione per tentativi. Consiste nel dividere il numero che vogliamo testare per tutti i numeri interi compresi tra 2 e la radice quadrata del numero stesso. Se nessuna di queste divisioni dà come resto zero, allora il numero è primo.

Ad esempio, per verificare se 37 è un numero primo, lo divideremmo per 2, 3, 4, 5 e 6 (perché la radice quadrata di 37 è circa 6.08). Nessuna di queste divisioni dà come resto zero, quindi 37 è un numero primo.

Questo metodo è più facile da implementare in un programma per computer, ma diventa rapidamente inefficiente per numeri molto grandi.

Perché i Numeri Primi Sono Così Importanti?

La vera magia dei numeri primi risiede nella loro capacità di essere i "mattoni" con cui si costruiscono tutti gli altri numeri. Questo è espresso dal Teorema Fondamentale dell'Aritmetica, che afferma che ogni numero intero maggiore di 1 può essere scritto in modo univoco come prodotto di numeri primi, a meno dell'ordine dei fattori.

Ad esempio, il numero 12 può essere scritto come 2 x 2 x 3 (o 2² x 3). Non esiste un'altra combinazione di numeri primi che possa dare 12 come risultato.

Questa proprietà rende i numeri primi fondamentali per la teoria dei numeri e ha implicazioni pratiche enormi.

Crittografia: Proteggere le Nostre Informazioni Online

Uno degli usi più importanti dei numeri primi è nella crittografia, la scienza di codificare le informazioni in modo che solo le persone autorizzate possano leggerle. Molti sistemi di crittografia moderni, come l'algoritmo RSA, si basano sulla difficoltà di fattorizzare numeri molto grandi in numeri primi.

In pratica, questo significa che se vuoi inviare un messaggio sicuro a qualcuno, puoi codificarlo usando una chiave pubblica (che è derivata da due numeri primi molto grandi). Solo la persona che possiede la chiave privata corrispondente (derivata anch'essa da quei numeri primi) sarà in grado di decodificare il messaggio. La sicurezza di questo sistema dipende dal fatto che fattorizzare numeri primi molto grandi è un compito computazionalmente impossibile con la tecnologia attuale.

Quindi, ogni volta che fai un acquisto online, accedi al tuo conto bancario o invii un'email, i numeri primi stanno lavorando silenziosamente in background per proteggere le tue informazioni.

Altre Applicazioni Pratiche

Oltre alla crittografia, i numeri primi hanno anche applicazioni in altri campi, tra cui:

• Generazione di numeri casuali: Molti algoritmi per generare numeri casuali si basano su proprietà dei numeri primi.
• Codici correttori di errore: I numeri primi sono usati per creare codici che possono rilevare e correggere errori nella trasmissione di dati.
• Fisica teorica: Alcuni modelli in fisica teorica utilizzano proprietà dei numeri primi per descrivere fenomeni complessi.
• Informatica: Nella progettazione di tabelle hash e algoritmi di ricerca.

Oltre il 100: Esplorando l'Infinito dei Numeri Primi

Abbiamo esplorato i numeri primi fino a 100, ma la verità è che i numeri primi sono infiniti. Questo è stato dimostrato da Euclide più di 2000 anni fa, in una delle dimostrazioni più eleganti e concisi della matematica.

La dimostrazione di Euclide si basa sulla riduzione all'assurdo. Supponiamo per assurdo che ci sia un numero finito di numeri primi: p₁, p₂, ..., pₙ. Consideriamo ora il numero N = (p₁ * p₂ * ... * pₙ) + 1. Questo numero N è o primo, o composto.

• Se N è primo, allora abbiamo trovato un nuovo numero primo che non era nella nostra lista originale, contraddicendo la nostra ipotesi.
• Se N è composto, allora deve essere divisibile per un numero primo. Ma N non è divisibile per nessuno dei numeri primi nella nostra lista originale (perché la divisione darebbe sempre un resto di 1). Quindi, esiste un altro numero primo che non era nella nostra lista originale, ancora una volta contraddicendo la nostra ipotesi.

In entrambi i casi, la nostra ipotesi che ci sia un numero finito di numeri primi porta a una contraddizione. Pertanto, l'ipotesi deve essere falsa, e ci sono infiniti numeri primi.

La ricerca di numeri primi sempre più grandi è un'attività affascinante e continua tutt'ora. Il numero primo più grande conosciuto, aggiornato a [inserire data aggiornamento], ha milioni di cifre e viene scoperto grazie a progetti di calcolo distribuito, dove migliaia di computer in tutto il mondo collaborano per risolvere questo problema complesso.

Conclusione

I numeri primi, apparentemente semplici, sono in realtà i pilastri fondamentali su cui si basa gran parte della matematica e dell'informatica moderna. Dalla crittografia che protegge le nostre comunicazioni online alla base di molti algoritmi complessi, i numeri primi sono ovunque, anche se spesso non ce ne rendiamo conto.

Spero che questo articolo ti abbia aiutato a riscoprire la bellezza e l'importanza dei numeri primi, e che ti abbia ispirato a esplorare ulteriormente questo affascinante ramo della matematica.