I Numeri Primi Da 1 A 100

Ti sei mai chiesto quali sono i mattoni fondamentali di tutti i numeri? Parliamo dei numeri primi, entità matematiche affascinanti che giocano un ruolo cruciale in diversi campi, dalla crittografia alla semplice comprensione dei numeri interi. In questo articolo, esploreremo i numeri primi da 1 a 100, svelandone le proprietà e capendo perché sono così importanti. Questo articolo è pensato per chiunque sia interessato alla matematica, studenti, appassionati o semplicemente curiosi di saperne di più sui numeri.

Cosa Sono i Numeri Primi?

Un numero primo è un numero intero maggiore di 1 che ha solo due divisori positivi: 1 e se stesso. In altre parole, un numero primo non può essere diviso esattamente da nessun altro numero tranne 1 e lui stesso. Ad esempio, 7 è un numero primo perché può essere diviso solo per 1 e 7. Il numero 4, invece, non è primo perché può essere diviso per 1, 2 e 4.

Definizione chiave: Un numero primo è un numero intero maggiore di 1 con esattamente due divisori: 1 e se stesso.

È importante notare che il numero 1 non è considerato un numero primo. La definizione di numero primo richiede esattamente due divisori, e 1 ha solo un divisore (se stesso).

Perché i Numeri Primi Sono Importanti?

I numeri primi sono i blocchi costitutivi di tutti gli altri numeri interi. Questo concetto è formalizzato dal Teorema Fondamentale dell'Aritmetica, che afferma che ogni intero maggiore di 1 può essere espresso in modo univoco come un prodotto di numeri primi (a meno dell'ordine dei fattori).

Ad esempio, il numero 12 può essere scomposto in 2 x 2 x 3 (o 2² x 3). I numeri 2 e 3 sono entrambi numeri primi, e questa è l'unica combinazione di numeri primi che moltiplicati insieme danno 12.

Ma l'importanza dei numeri primi va oltre la pura teoria matematica. Sono fondamentali nella crittografia moderna. Molti algoritmi di crittografia, come RSA, si basano sulla difficoltà di fattorizzare numeri molto grandi in numeri primi. In altre parole, è facile moltiplicare due numeri primi enormi per ottenere un numero ancora più grande, ma è estremamente difficile, anche per i computer più potenti, determinare quali sono i due numeri primi originali partendo dal loro prodotto. Questa difficoltà è ciò che rende sicure molte delle nostre comunicazioni online.

I Numeri Primi da 1 a 100

Ora concentriamoci sui numeri primi compresi tra 1 e 100. Trovarli manualmente può essere un po' noioso, ma esiste un metodo semplice chiamato Crivello di Eratostene.

Il Crivello di Eratostene

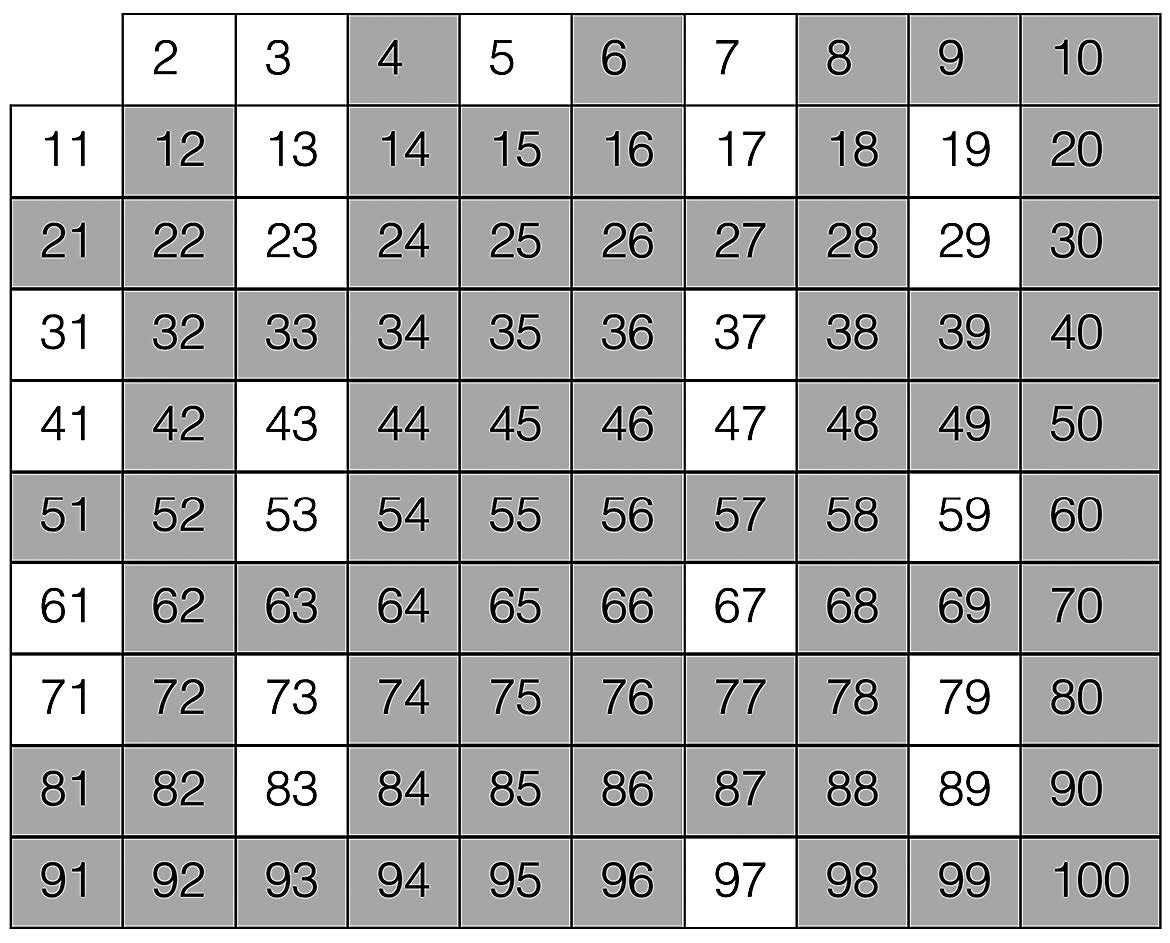
Il Crivello di Eratostene è un antico algoritmo per trovare tutti i numeri primi fino a un certo limite. Ecco come funziona:

Scrivi tutti i numeri interi da 2 fino al limite desiderato (in questo caso, 100).
Il primo numero della lista (2) è un numero primo. Cerchialo.
Cancella tutti i multipli di 2 (4, 6, 8, 10, ecc.) fino a 100.
Il numero successivo non cancellato nella lista (3) è un numero primo. Cerchialo.
Cancella tutti i multipli di 3 (6, 9, 12, 15, ecc.) fino a 100. Nota che alcuni di questi numeri (come 6) sono già stati cancellati.
Continua questo processo, cerchiando il numero successivo non cancellato (che sarà sempre un numero primo) e cancellando tutti i suoi multipli.
Quando arrivi a un numero il cui quadrato è maggiore del limite (in questo caso, 100), tutti i numeri non cancellati nella lista sono numeri primi.

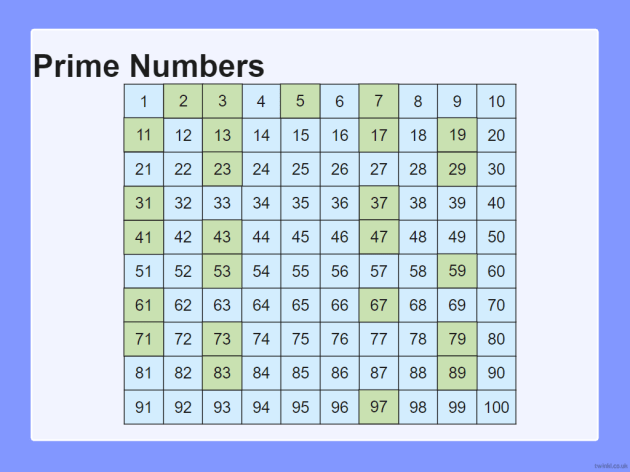
Utilizzando il Crivello di Eratostene, possiamo identificare i seguenti numeri primi tra 1 e 100:

Ci sono 25 numeri primi tra 1 e 100.

Pattern e Curiosità

Anche se i numeri primi sembrano distribuiti in modo casuale, ci sono alcuni pattern e curiosità interessanti da considerare:

Gap tra i numeri primi: Noterai che la distanza tra i numeri primi diventa in media più grande man mano che ci si sposta verso numeri più grandi. Ad esempio, i numeri primi 2 e 3 sono consecutivi, ma tra 89 e 97 c'è un gap di 8 numeri.
Numeri primi gemelli: Coppie di numeri primi che differiscono di 2 (come 3 e 5, 5 e 7, 11 e 13) sono chiamati numeri primi gemelli. La congettura dei numeri primi gemelli afferma che ci sono infiniti numeri primi gemelli, ma questa congettura non è ancora stata provata.
Distribuzione dei numeri primi: La distribuzione dei numeri primi è un argomento di studio attivo in matematica. Il Teorema dei Numeri Primi fornisce una stima della densità dei numeri primi: approssimativamente, ci sono circa n / ln(n) numeri primi minori di n.

Come Riconoscere i Numeri Primi?

Come facciamo a determinare se un numero è primo, specialmente quando si tratta di numeri più grandi? Oltre al Crivello di Eratostene, esistono diversi metodi, anche se diventano sempre più complessi con l'aumentare della dimensione del numero.

Divisione per prova: Il metodo più semplice è provare a dividere il numero per tutti i numeri interi da 2 fino alla sua radice quadrata. Se nessuno di questi numeri lo divide esattamente, allora è un numero primo. Ad esempio, per verificare se 37 è primo, proviamo a dividerlo per 2, 3, 4, 5 e 6. Nessuno di questi numeri lo divide esattamente, quindi 37 è un numero primo.
Test di primalità: Esistono algoritmi più sofisticati chiamati test di primalità, come il test di Miller-Rabin, che possono determinare se un numero è probabilmente primo con un'alta probabilità. Questi test sono utilizzati nella crittografia per generare numeri primi molto grandi.

I Numeri Primi Nella Vita Reale

Anche se potresti non pensare ai numeri primi nella tua vita quotidiana, come abbiamo già detto, sono essenziali per la sicurezza di internet. Ogni volta che effettui un acquisto online, invii un'email o utilizzi un bancomat, i numeri primi sono al lavoro dietro le quinte per proteggere le tue informazioni.

Inoltre, i numeri primi trovano applicazioni in:

Generazione di numeri casuali: Alcuni algoritmi di generazione di numeri casuali utilizzano numeri primi per garantire che i numeri generati siano il più possibile imprevedibili.
Teoria dei codici: I numeri primi sono utilizzati nella costruzione di codici di correzione degli errori, che vengono utilizzati per rilevare e correggere errori nella trasmissione dei dati.
Musica e arte: Alcuni compositori e artisti hanno utilizzato numeri primi per creare strutture e pattern nelle loro opere.

Conclusione

I numeri primi, apparentemente semplici, sono in realtà entità matematiche potenti con implicazioni profonde in diverse aree della scienza e della tecnologia. Comprendere i numeri primi da 1 a 100 è un ottimo punto di partenza per esplorare il mondo affascinante della teoria dei numeri. Speriamo che questo articolo ti abbia fornito una solida base e ti abbia ispirato a saperne di più sui numeri primi e le loro molteplici applicazioni. Continua a esplorare, a domandare e a scoprire le meraviglie della matematica!