I Divisori Di 15 Quali Sono
Comprendere i divisori di un numero è un concetto fondamentale in matematica, che si applica non solo in ambito scolastico, ma anche in diverse situazioni della vita reale. In questo articolo, esploreremo in dettaglio i divisori del numero 15, analizzando cosa sono, come identificarli e perché sono importanti.
Cosa Sono i Divisori?
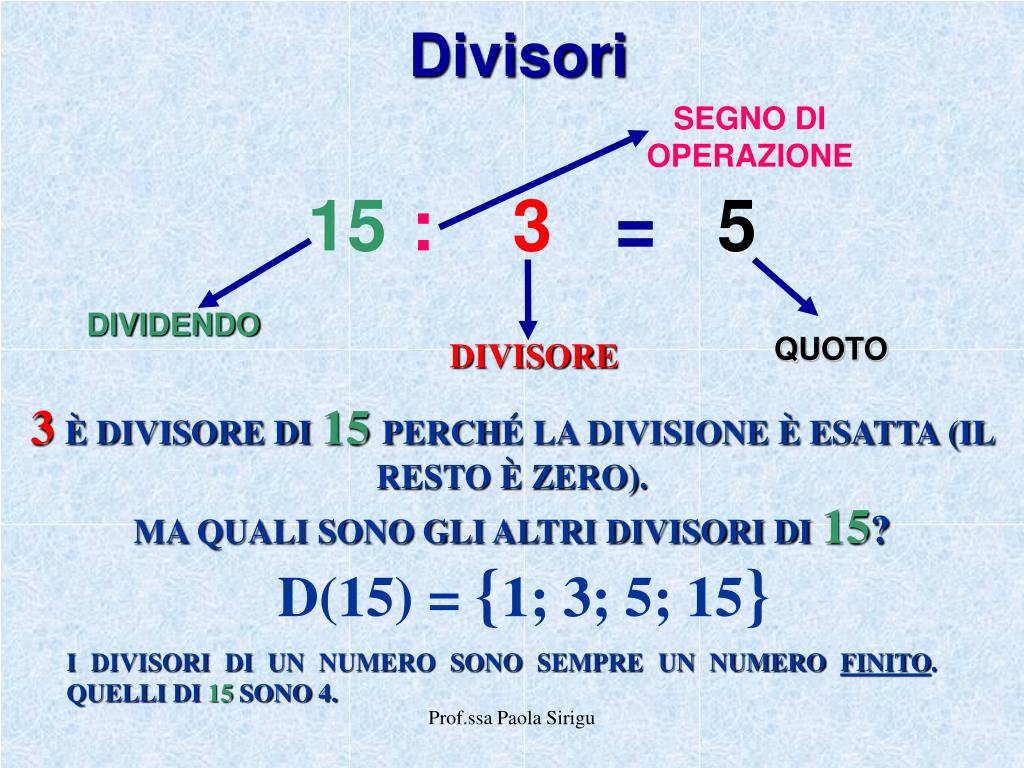
Un divisore di un numero intero è un altro numero intero che lo divide esattamente, senza lasciare resto. In altre parole, se dividiamo un numero per un suo divisore, il risultato è un altro numero intero. Ad esempio, 3 è un divisore di 12 perché 12 ÷ 3 = 4, che è un numero intero.
Definizione formale: Un numero intero a è un divisore di un numero intero b se esiste un numero intero c tale che b = a × c.
Come Trovare i Divisori di un Numero
Esistono diversi metodi per trovare i divisori di un numero. Il metodo più semplice è provare a dividere il numero per tutti gli interi positivi inferiori o uguali alla sua radice quadrata. Se la divisione dà un risultato intero, allora sia il divisore che il risultato della divisione sono divisori del numero originale.
Esempio: Per trovare i divisori di 15, possiamo procedere come segue:
* Dividiamo 15 per 1: 15 ÷ 1 = 15 (1 e 15 sono divisori). * Dividiamo 15 per 2: 15 ÷ 2 = 7.5 (2 non è un divisore perché il risultato non è un intero). * Dividiamo 15 per 3: 15 ÷ 3 = 5 (3 e 5 sono divisori). * Dividiamo 15 per 4: 15 ÷ 4 = 3.75 (4 non è un divisore).Notiamo che la radice quadrata di 15 è circa 3.87. Abbiamo controllato fino a 3 e trovato tutti i divisori minori della radice quadrata. Non è necessario controllare oltre perché i divisori maggiori si troveranno automaticamente (come 5 e 15 nel nostro esempio).
I Divisori di 15
Applicando il metodo descritto sopra, possiamo determinare che i divisori di 15 sono: 1, 3, 5 e 15. Questi sono gli unici numeri interi positivi che dividono 15 senza lasciare resto.
È importante ricordare che 1 e il numero stesso sono sempre divisori di qualsiasi numero intero (diverso da zero).
Divisori Positivi e Negativi
Tecnicamente, anche i numeri negativi possono essere divisori. Se un numero positivo è un divisore, anche il suo negativo lo è. Quindi, i divisori di 15 includono anche -1, -3, -5 e -15. Tuttavia, quando si parla semplicemente di "divisori", si intendono solitamente quelli positivi.
Perché Conoscere i Divisori è Importante?
La conoscenza dei divisori è fondamentale in diversi contesti matematici e pratici:
* Fattorizzazione: I divisori sono la base per la fattorizzazione di un numero, ovvero la sua scomposizione in fattori primi. Ad esempio, 15 = 3 × 5. * Massimo Comune Divisore (MCD): Per calcolare il MCD tra due o più numeri, è necessario conoscere i loro divisori comuni. * Minimo Comune Multiplo (MCM): Analogamente, il MCM si calcola utilizzando i divisori e i fattori primi dei numeri in questione. * Frazioni: La semplificazione delle frazioni richiede l'identificazione di divisori comuni tra numeratore e denominatore. * Algebra: La risoluzione di equazioni e la manipolazione di espressioni algebriche spesso coinvolgono la conoscenza dei divisori. * Crittografia: In alcuni algoritmi crittografici, la difficoltà di fattorizzare numeri grandi in fattori primi (ovvero trovare i loro divisori) è alla base della sicurezza del sistema.Esempi Pratici
Ecco alcuni esempi di come i divisori di 15 possono essere utilizzati in situazioni reali:
* Suddivisione di un gruppo: Immagina di avere 15 studenti e di volerli dividere in gruppi uguali. I divisori di 15 (1, 3, 5 e 15) ti dicono che puoi formare 1 gruppo da 15, 3 gruppi da 5, 5 gruppi da 3, o 15 gruppi da 1. * Organizzazione di oggetti: Hai 15 oggetti (ad esempio, caramelle) e vuoi disporli in file uguali. Ancora una volta, i divisori di 15 ti aiutano a determinare le possibili configurazioni. Puoi fare 1 fila da 15, 3 file da 5, 5 file da 3 o 15 file da 1. * Pianificazione di attività: Devi completare 15 compiti e vuoi distribuirli uniformemente su diversi giorni. I divisori di 15 ti dicono quanti compiti puoi fare al giorno se vuoi completarli in un numero intero di giorni (1 compito al giorno per 15 giorni, 3 compiti al giorno per 5 giorni, 5 compiti al giorno per 3 giorni, o 15 compiti al giorno per 1 giorno).Il Numero 15 e i Numeri Primi
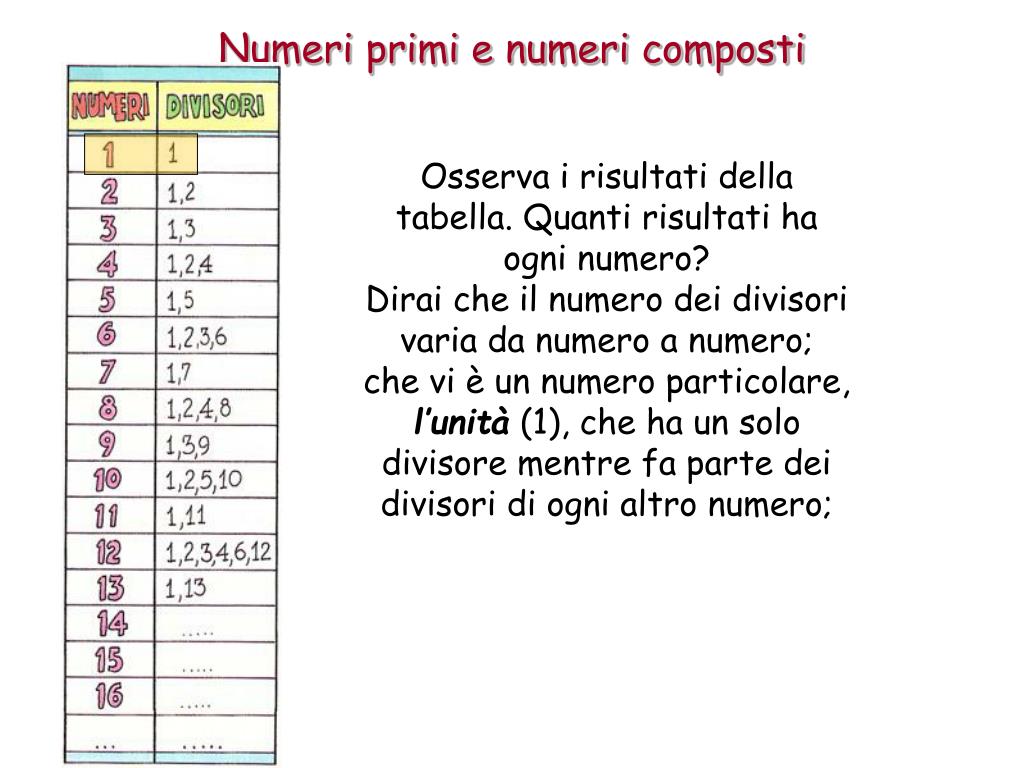
Un numero primo è un numero intero maggiore di 1 che ha solo due divisori: 1 e se stesso. Ad esempio, 2, 3, 5, 7, 11 sono numeri primi.
Il numero 15 non è un numero primo perché ha quattro divisori: 1, 3, 5 e 15. Un numero che ha più di due divisori è chiamato numero composto. 15 è un esempio di numero composto.
La fattorizzazione prima di 15 è 3 × 5. Questo significa che 15 può essere espresso come il prodotto di due numeri primi.
La Regola di Divisibilità per 3 e 5
Conoscere le regole di divisibilità rende più facile individuare i divisori di un numero. Per il numero 15, ci sono due regole importanti da considerare:
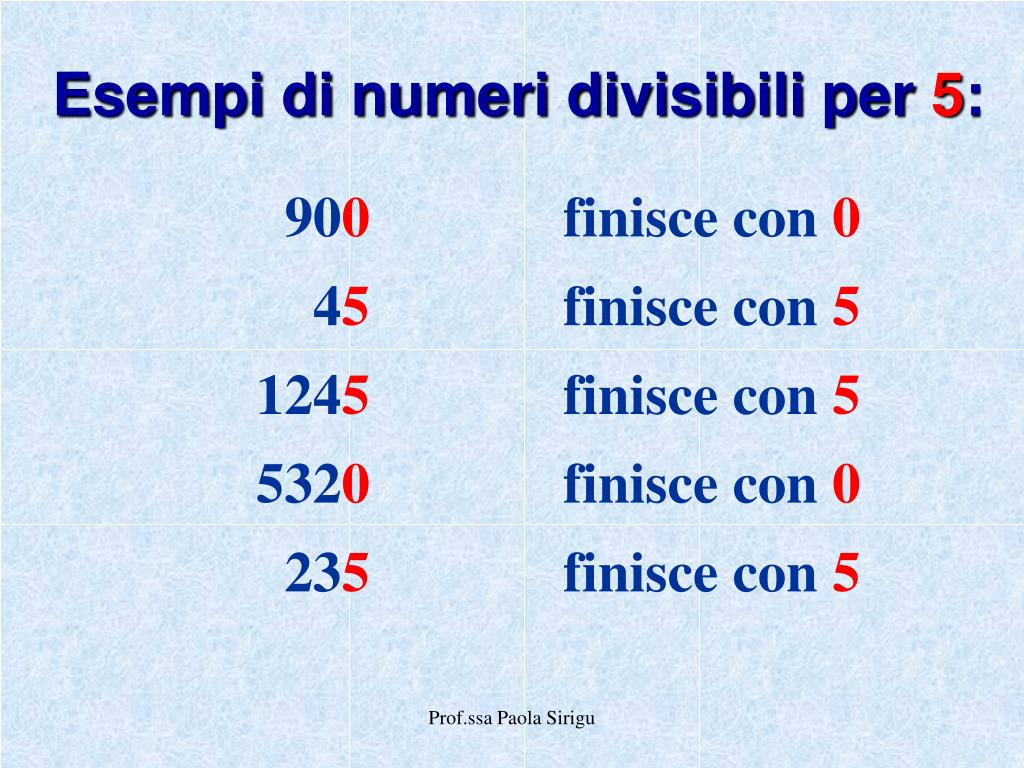
* Divisibilità per 3: Un numero è divisibile per 3 se la somma delle sue cifre è divisibile per 3. Nel caso di 15, la somma delle cifre è 1 + 5 = 6, che è divisibile per 3. Quindi, 15 è divisibile per 3. * Divisibilità per 5: Un numero è divisibile per 5 se la sua ultima cifra è 0 o 5. Poiché l'ultima cifra di 15 è 5, 15 è divisibile per 5.Approfondimento: Divisori e Applicazioni Avanzate
Oltre alle applicazioni di base menzionate, i divisori giocano un ruolo cruciale in aree più avanzate della matematica e dell'informatica:
* Teoria dei Numeri: La teoria dei numeri è un ramo della matematica che studia le proprietà dei numeri interi, inclusi i divisori, i numeri primi, le congruenze e le equazioni diofantine. * Algebra Modulare: L'algebra modulare, che coinvolge le operazioni sui resti della divisione, è strettamente legata ai divisori e trova applicazioni nella crittografia e nella codifica. * Algoritmi: Molti algoritmi, specialmente quelli relativi alla ricerca, all'ordinamento e alla compressione dei dati, utilizzano concetti legati ai divisori e alla fattorizzazione. * Grafica Computerizzata: La suddivisione di oggetti e superfici in elementi più piccoli per la visualizzazione grafica spesso si basa su principi legati alla divisibilità.Conclusione
Abbiamo visto che i divisori di 15 sono 1, 3, 5 e 15. La comprensione dei divisori non è solo un esercizio matematico, ma una competenza utile in molte situazioni quotidiane e in discipline più avanzate. Imparare a identificare i divisori di un numero, comprenderne il significato e applicarli in contesti diversi può migliorare la tua capacità di risolvere problemi e affrontare sfide in modo più efficace.
Ti invitiamo a continuare ad esplorare il mondo dei numeri e delle loro proprietà. Prova a trovare i divisori di altri numeri, come 24, 36 o 48, e cerca di applicare le regole di divisibilità che hai imparato. Più ti eserciti, più diventerai abile nell'identificare i divisori e comprenderne l'importanza.