Geometria Analitica Nello Spazio Esercizi Svolti Pdf

Quante volte ti sei trovato a fissare un esercizio di geometria analitica nello spazio, sentendo un nodo alla gola e una frustrazione crescente? Non sei solo! Molti studenti, e persino professionisti, si scontrano con la difficoltà di visualizzare e manipolare oggetti in tre dimensioni utilizzando le coordinate.

La geometria analitica nello spazio, con le sue equazioni di piani, rette e superfici, può sembrare un labirinto inestricabile. Ma la verità è che, con la giusta guida e un approccio metodico, si può trasformare in uno strumento potente per risolvere problemi complessi e sviluppare una comprensione più profonda del mondo che ci circonda.

Perché la Geometria Analitica Nello Spazio è Importante?

Prima di immergerci negli esercizi svolti, è fondamentale capire perché questo ramo della matematica è così cruciale. La geometria analitica nello spazio non è solo un esercizio accademico; ha applicazioni pratiche innumerevoli:

Ingegneria: Progettazione di strutture, modellazione di oggetti 3D, simulazioni di fluidodinamica.
Grafica computerizzata: Creazione di mondi virtuali, rendering di immagini realistiche, animazione 3D.
Fisica: Studio del movimento dei corpi nello spazio, analisi di campi vettoriali, modellazione di fenomeni naturali.
Architettura: Progettazione di edifici, calcolo di volumi e superfici, visualizzazione di spazi interni ed esterni.
Medicina: Imaging diagnostico (TAC, risonanza magnetica), pianificazione di interventi chirurgici, modellazione di organi e tessuti.

Come puoi vedere, la capacità di pensare e risolvere problemi in tre dimensioni è un'abilità preziosa in molti campi. Per questo motivo, padroneggiare la geometria analitica nello spazio può aprirti molte porte.

Il Tuo Alleato: Esercizi Svolti in PDF

Uno degli strumenti più efficaci per superare le difficoltà della geometria analitica nello spazio è lo studio degli esercizi svolti. Avere a disposizione esempi concreti, con la spiegazione passo-passo del procedimento risolutivo, permette di:

Comprendere i concetti: Vedere come vengono applicate le formule e i teoremi in situazioni reali.
Sviluppare la logica: Analizzare il ragionamento che porta alla soluzione.
Acquisire sicurezza: Imparare a riconoscere i diversi tipi di problemi e ad applicare le strategie corrette.
Evitare errori comuni: Confrontare il proprio procedimento con quello corretto e individuare le lacune.

Un buon PDF di esercizi svolti dovrebbe includere una varietà di problemi, dai più semplici ai più complessi, coprendo tutti gli argomenti fondamentali della geometria analitica nello spazio.

Argomenti Chiave e Esercizi Tipo

Ecco alcuni degli argomenti più importanti che dovresti cercare in un PDF di esercizi svolti, insieme a esempi di problemi tipo:

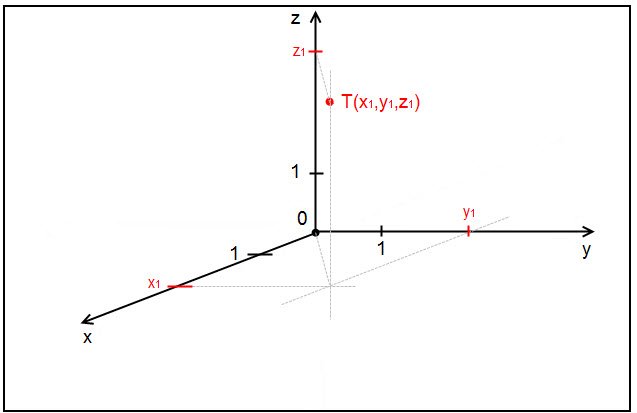
1. Vettori nello Spazio

Concetti chiave: Rappresentazione di vettori, operazioni con vettori (somma, differenza, prodotto scalare, prodotto vettoriale), versori, modulo di un vettore, angolo tra due vettori.

Esercizio tipo: Dati i punti A(1, 2, 3) e B(4, 5, 6), determinare il vettore AB, il suo modulo e il versore associato. Calcolare l'angolo tra il vettore AB e il vettore v = (2, -1, 0).

2. Rette nello Spazio

Concetti chiave: Equazione parametrica di una retta, equazione cartesiana di una retta, vettore direzione, punto di passaggio, posizione reciproca di due rette (parallele, incidenti, sghembe), distanza di un punto da una retta.

Esercizio tipo: Determinare l'equazione parametrica della retta passante per i punti A(1, 0, -1) e B(2, 1, 0). Stabilire se la retta è parallela al piano di equazione x + y - z = 0.

3. Piani nello Spazio

Concetti chiave: Equazione cartesiana di un piano, vettore normale, punto di passaggio, posizione reciproca di due piani (paralleli, incidenti), distanza di un punto da un piano, angolo tra due piani.

Esercizio tipo: Determinare l'equazione del piano passante per il punto P(1, 1, 1) e perpendicolare al vettore v = (2, -1, 3). Calcolare la distanza del punto Q(0, 0, 0) dal piano.

4. Superfici

Concetti chiave: Sfere, cilindri, coni, paraboloidi, iperboloidi, ellissoidi. Equazioni canoniche e loro traslazioni e rotazioni.

Esercizio tipo: Individuare il tipo di superficie rappresentata dall'equazione x² + y² + z² - 2x + 4y - 6z = 0. Determinarne il centro e il raggio (nel caso di una sfera).

Come Sfruttare al Meglio gli Esercizi Svolti

Non limitarti a leggere passivamente gli esercizi svolti. Per ottenere il massimo beneficio, segui questi consigli:

Prova a risolvere il problema da solo: Prima di guardare la soluzione, cerca di affrontare il problema con le tue forze. Anche se non riesci a risolverlo completamente, questo ti aiuterà a identificare le tue difficoltà e a capire meglio la soluzione proposta.
Analizza la soluzione passo-passo: Concentrati sul ragionamento che porta alla soluzione. Cerca di capire perché è stata scelta una determinata strategia e come sono state applicate le formule.
Verifica la soluzione: Controlla che la soluzione ottenuta sia corretta, sostituendo i valori trovati nell'equazione originale o utilizzando altri metodi.
Rifai l'esercizio senza guardare la soluzione: Dopo aver studiato la soluzione, prova a rifare l'esercizio da solo, senza consultare il PDF. Questo ti aiuterà a consolidare le tue conoscenze e a sviluppare la tua autonomia.
Cerca esercizi simili: Una volta che hai capito come risolvere un determinato tipo di problema, cerca altri esercizi simili e prova a risolverli da solo. Questo ti aiuterà a generalizzare le tue conoscenze e a sviluppare la tua capacità di problem solving.

Dove Trovare PDF di Esercizi Svolti di Geometria Analitica Nello Spazio

Esistono diverse risorse online dove puoi trovare PDF di esercizi svolti di geometria analitica nello spazio:

Siti web di università e scuole superiori: Molte istituzioni pubblicano online materiale didattico, tra cui esercizi svolti e temi d'esame.
Forum e community online: Esistono forum dedicati alla matematica dove puoi trovare esercizi svolti e chiedere aiuto a altri studenti e appassionati.
Libri di testo e eserciziari: Molti libri di testo di geometria analitica contengono esercizi svolti. In alternativa, puoi acquistare un eserciziario specifico.
Motori di ricerca: Utilizzando parole chiave come "esercizi svolti geometria analitica spazio pdf" puoi trovare una vasta gamma di risorse online.

Ricorda di valutare attentamente la qualità del materiale che trovi online. Assicurati che gli esercizi siano risolti correttamente e che le spiegazioni siano chiare e comprensibili. Non esitare a consultare diverse fonti per avere una visione più completa e approfondita.

Oltre gli Esercizi: Consigli Aggiuntivi

Oltre allo studio degli esercizi svolti, ecco alcuni consigli aggiuntivi per migliorare la tua comprensione della geometria analitica nello spazio:

Visualizza gli oggetti: Cerca di immaginare gli oggetti geometrici nello spazio. Disegna schizzi e modelli per aiutarti a visualizzare le relazioni tra punti, rette, piani e superfici.
Utilizza software di geometria dinamica: Esistono software gratuiti che ti permettono di visualizzare e manipolare oggetti geometrici in tre dimensioni. Questi strumenti possono aiutarti a sviluppare la tua intuizione spaziale.
Collabora con altri studenti: Studiare insieme ad altri studenti può aiutarti a comprendere meglio i concetti e a risolvere i problemi più difficili. Scambiatevi idee, discutete le soluzioni e aiutatevi a vicenda.
Non avere paura di chiedere aiuto: Se ti trovi in difficoltà, non esitare a chiedere aiuto al tuo insegnante, a un tutor o a altri studenti.
Sii paziente e perseverante: La geometria analitica nello spazio può essere difficile, ma con la pratica e la perseveranza puoi superare le tue difficoltà e padroneggiare questo affascinante ramo della matematica.

La chiave per il successo nella geometria analitica nello spazio è la pratica costante e un approccio metodico. Con gli esercizi svolti in PDF come tuo alleato, e seguendo i consigli che ti ho dato, sarai in grado di superare le tue difficoltà e di sbloccare il tuo potenziale.

Ricorda: la matematica è come uno sport. Più ti alleni, più diventi bravo. Quindi, non arrenderti e continua a esercitarti! Buon lavoro!