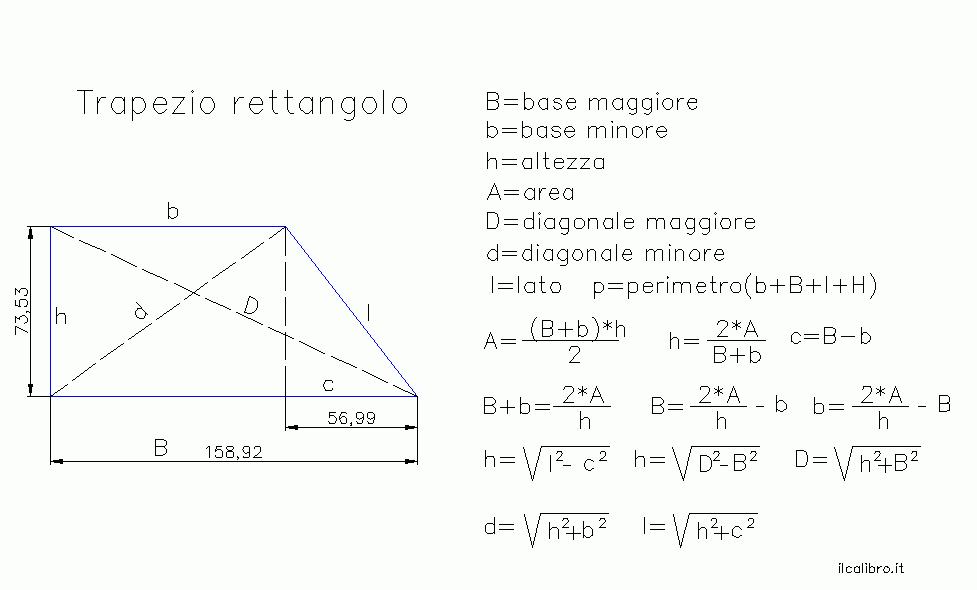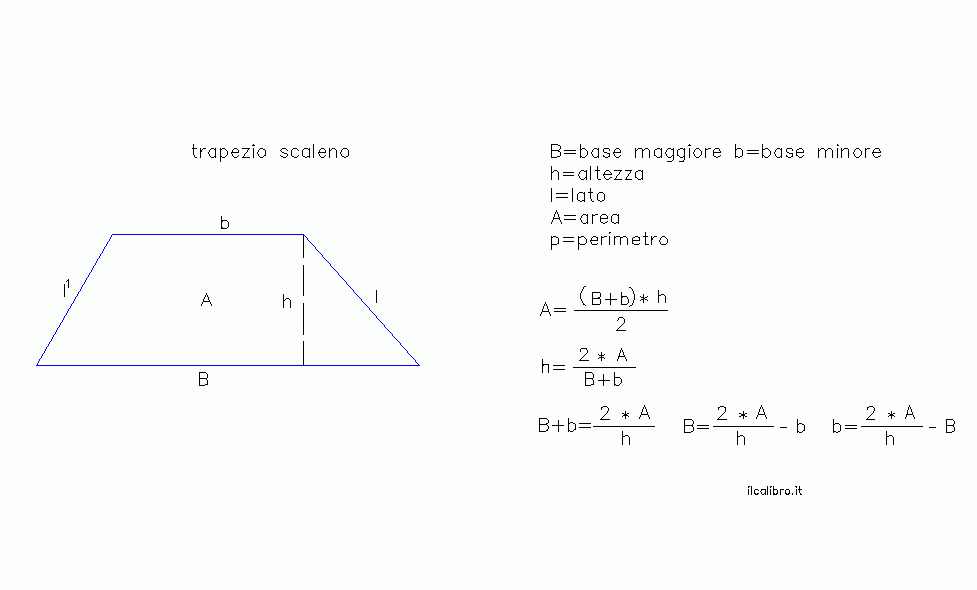Formula Per Calcolare L'area Del Trapezio

Il trapezio è una figura geometrica a quattro lati, o quadrilatero, caratterizzato da due lati paralleli, chiamati basi (una base maggiore e una base minore), e due lati non paralleli, detti lati obliqui. Capire come calcolare la sua area è fondamentale in numerosi campi, dalla geometria pratica all'architettura e all'ingegneria. Questo articolo esplorerà in dettaglio la formula per calcolare l'area del trapezio, fornendo spiegazioni chiare, esempi pratici e applicazioni reali.

Comprendere la Formula dell'Area del Trapezio

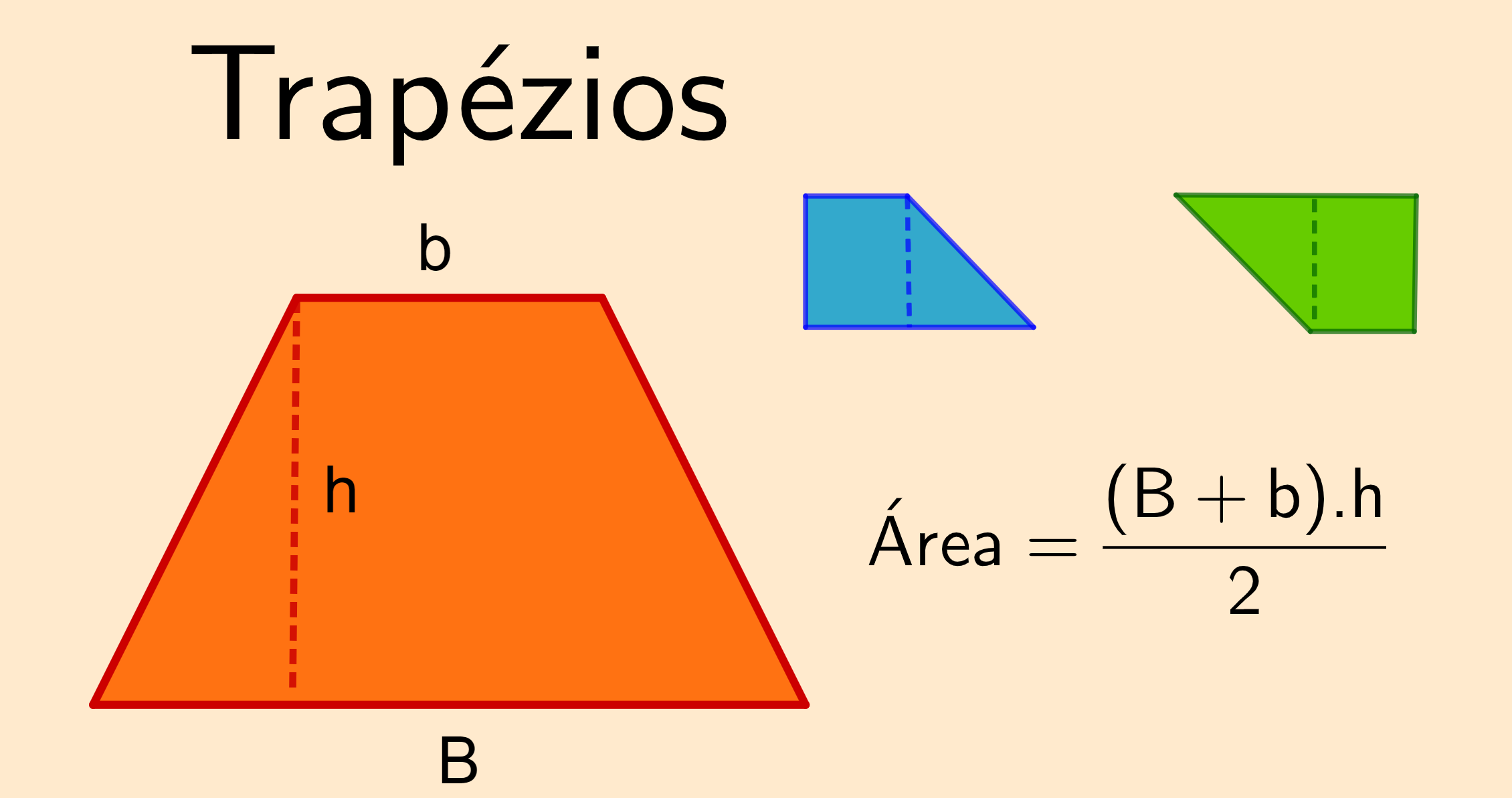
La formula per calcolare l'area del trapezio è piuttosto semplice, una volta compresi i concetti di base. L'area di un trapezio si ottiene moltiplicando la somma delle lunghezze delle due basi per l'altezza e dividendo il risultato per due. Matematicamente, possiamo esprimere questa formula come:

Area = (Base Maggiore + Base Minore) * Altezza / 2

Dove:

• Base Maggiore è la lunghezza del lato parallelo più lungo del trapezio.
• Base Minore è la lunghezza del lato parallelo più corto del trapezio.
• Altezza è la distanza perpendicolare tra le due basi.

È cruciale assicurarsi che tutte le misure siano espresse nella stessa unità di misura prima di applicare la formula. Ad esempio, se le basi sono misurate in centimetri, l'altezza deve essere anch'essa in centimetri per ottenere l'area in centimetri quadrati.

Perché Funziona Questa Formula?

La ragione per cui questa formula funziona può essere compresa immaginando di dividere il trapezio in figure geometriche più semplici. Possiamo pensare di suddividere il trapezio in un rettangolo e due triangoli (o un triangolo se i lati obliqui sono paralleli). L'area del rettangolo sarebbe data dalla base minore moltiplicata per l'altezza, mentre l'area dei due triangoli sarebbe data dalla somma delle aree dei singoli triangoli. Sommare l'area del rettangolo all'area dei triangoli porterebbe allo stesso risultato della formula del trapezio.

Un altro modo per visualizzare la formula è considerare il trapezio come la "media" di un rettangolo. La lunghezza del lato del rettangolo sarebbe la media delle due basi del trapezio (Base Maggiore + Base Minore) / 2. Moltiplicando questa "base media" per l'altezza, otteniamo l'area del trapezio.

Passaggi per Calcolare l'Area del Trapezio

Calcolare l'area del trapezio richiede solo alcuni passaggi semplici:

1. Identificare le basi: Determina quali sono i lati paralleli del trapezio e misurane le lunghezze. Chiameremo il lato più lungo "Base Maggiore" e il lato più corto "Base Minore".
2. Misurare l'altezza: L'altezza è la distanza perpendicolare tra le due basi. Misura questa distanza.
3. Applicare la formula: Inserisci le misurazioni nella formula Area = (Base Maggiore + Base Minore) * Altezza / 2.
4. Calcolare l'area: Esegui i calcoli per ottenere l'area del trapezio. Ricorda di includere l'unità di misura appropriata (ad esempio, centimetri quadrati, metri quadrati, ecc.).

Ad esempio, consideriamo un trapezio con Base Maggiore = 10 cm, Base Minore = 6 cm e Altezza = 5 cm. L'area sarebbe:

Area = (10 cm + 6 cm) * 5 cm / 2 = 16 cm * 5 cm / 2 = 80 cm² / 2 = 40 cm²

Quindi, l'area di questo trapezio è di 40 centimetri quadrati.

Cosa Fare se l'Altezza Non è Nota

In alcuni casi, l'altezza del trapezio potrebbe non essere fornita direttamente. Potrebbe essere necessario utilizzare altre informazioni, come la lunghezza dei lati obliqui e gli angoli, per calcolare l'altezza. La trigonometria può essere uno strumento utile in queste situazioni.

Se conosciamo la lunghezza di un lato obliquo e l'angolo che forma con una delle basi, possiamo utilizzare le funzioni trigonometriche seno o coseno per trovare l'altezza. Ad esempio, se conosciamo l'angolo α tra il lato obliquo e la base maggiore, e la lunghezza del lato obliquo (l), l'altezza (h) può essere calcolata come:

h = l * sin(α)

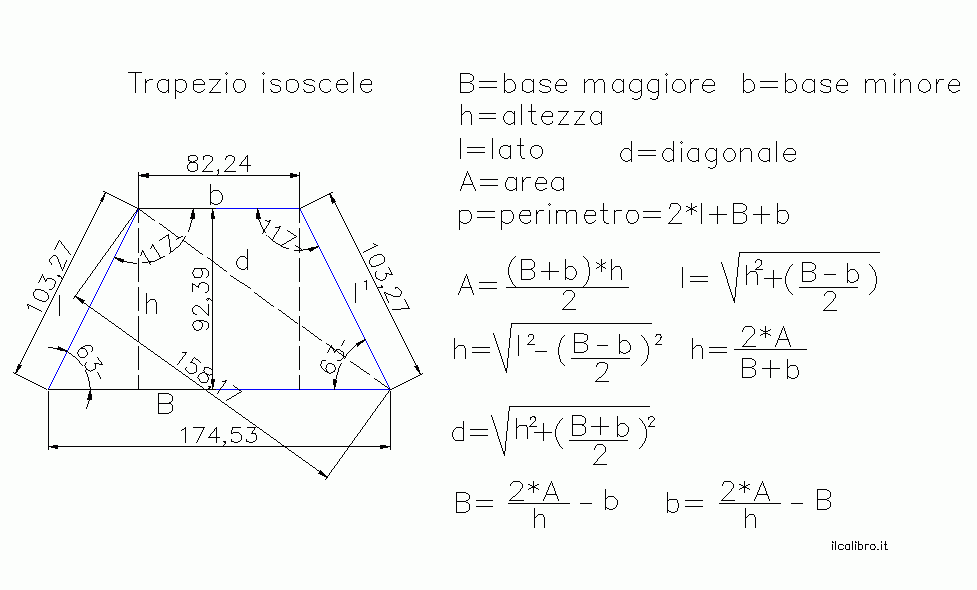
Alternativamente, se il trapezio è isoscele (i lati obliqui sono congruenti), si può tracciare l'altezza da entrambi i vertici della base minore sulla base maggiore. In questo modo, si formano due triangoli rettangoli congruenti e un rettangolo. Utilizzando il teorema di Pitagora applicato a uno dei triangoli rettangoli, e conoscendo la lunghezza del lato obliquo e la differenza tra le due basi divisa per due, si può calcolare l'altezza.

Esempi Reali e Applicazioni Pratiche

La formula per calcolare l'area del trapezio trova applicazione in una vasta gamma di scenari reali:

• Architettura: Gli architetti spesso utilizzano trapezi per progettare tetti, finestre e altre strutture. Calcolare l'area di queste superfici è essenziale per stimare i costi dei materiali e la quantità di lavoro necessaria. Ad esempio, il tetto di una casa potrebbe avere una forma trapezoidale, e la conoscenza dell'area è cruciale per calcolare la quantità di tegole necessarie.
• Ingegneria Civile: Nella costruzione di strade e ponti, i trapezi sono spesso utilizzati per la progettazione di sezioni trasversali. Calcolare l'area di queste sezioni è fondamentale per determinare il volume di materiali necessari, come l'asfalto o il cemento.
• Agricoltura: I campi agricoli possono avere forme irregolari, compresi i trapezi. Gli agricoltori devono calcolare l'area dei loro campi per stimare la quantità di fertilizzanti e sementi necessarie, nonché la resa prevista del raccolto.
• Design: I designer possono utilizzare trapezi in vari progetti, dalla creazione di loghi alla progettazione di interni. Calcolare l'area dei trapezi è utile per garantire che gli elementi del design siano proporzionati e visivamente accattivanti. Ad esempio, una piastrella con forma trapezoidale può essere utilizzata per creare pavimenti o rivestimenti murali.
• Geodesia e Cartografia: Nella misurazione e rappresentazione del territorio, i trapezi possono essere utilizzati per approssimare aree con confini irregolari. La formula del trapezio fornisce un metodo semplice ed efficace per stimare l'area di tali regioni.

Consideriamo, ad esempio, la stima della quantità di vernice necessaria per dipingere una parete trapezoidale. Supponiamo che la parete abbia una base maggiore di 5 metri, una base minore di 3 metri e un'altezza di 2,5 metri. L'area della parete sarebbe:

Area = (5 m + 3 m) * 2,5 m / 2 = 8 m * 2,5 m / 2 = 20 m² / 2 = 10 m²

Sapendo che un litro di vernice copre circa 8 metri quadrati, avremmo bisogno di circa 1,25 litri di vernice per dipingere la parete. Questo semplice calcolo, basato sulla formula dell'area del trapezio, ci permette di stimare con precisione la quantità di materiale necessario, evitando sprechi e risparmiando denaro.

Variazioni e Considerazioni Speciali

È importante notare che esistono diversi tipi di trapezi:

• Trapezio Isoscele: Un trapezio con i lati obliqui congruenti. Questo tipo di trapezio ha proprietà speciali, come angoli alla base congruenti.
• Trapezio Rettangolo: Un trapezio con almeno un angolo retto. In questo caso, uno dei lati obliqui coincide con l'altezza.
• Trapezio Scaleno: Un trapezio con tutti i lati di lunghezza diversa.

La formula per l'area del trapezio funziona per tutti i tipi di trapezi, indipendentemente dalla loro forma. Tuttavia, in alcuni casi, le proprietà specifiche di un particolare tipo di trapezio possono semplificare il calcolo dell'area. Ad esempio, in un trapezio rettangolo, l'altezza è semplicemente la lunghezza del lato perpendicolare alle basi.

Un'altra considerazione importante è la precisione delle misurazioni. L'accuratezza del calcolo dell'area dipende dalla precisione delle misure delle basi e dell'altezza. Piccoli errori nelle misurazioni possono portare a errori significativi nel calcolo dell'area, soprattutto quando le dimensioni del trapezio sono grandi.

Conclusione

La formula per calcolare l'area del trapezio è uno strumento fondamentale nella geometria e nelle sue applicazioni pratiche. Comprendere la formula, i passaggi per applicarla e le sue variazioni è essenziale per risolvere una vasta gamma di problemi reali. Dalle costruzioni all'agricoltura, dal design all'ingegneria, la capacità di calcolare l'area di un trapezio si rivela preziosa.

Sperimenta con diversi esempi e pratica l'applicazione della formula per affinare le tue capacità. Ricorda, la chiave per la padronanza è la pratica costante e la comprensione dei concetti fondamentali. Continua a esplorare e ad applicare la geometria nella tua vita quotidiana! Buon calcolo!