Formula Della Circonferenza Di Un Cerchio

Quante volte ti sei trovato di fronte a un cerchio, magari guardando una pizza, una ruota di bicicletta o il quadrante di un orologio, chiedendoti come calcolare la sua circonferenza? Capire la formula della circonferenza di un cerchio non è solo un esercizio matematico astratto; è una competenza fondamentale che si applica a innumerevoli situazioni reali. Magari devi recintare un'area circolare nel tuo giardino, oppure calcolare quanti giri farà una ruota durante un determinato percorso. La matematica, spesso percepita come ostica, in realtà ci offre strumenti potentissimi per comprendere e interagire con il mondo che ci circonda.

Perché è importante conoscere la formula della circonferenza?

La formula della circonferenza non è un enigma da risolvere per superare un esame. È un mattone fondamentale per costruire la nostra comprensione del mondo. Pensa solo a come le ruote, una delle invenzioni più importanti della storia, dipendono intrinsecamente dal principio della circonferenza. Senza la capacità di calcolare la distanza percorsa da una ruota in una rotazione, i progressi nei trasporti sarebbero stati drasticamente limitati. Ma l'importanza va oltre l'ingegneria. In astronomia, la circonferenza è essenziale per calcolare le orbite dei pianeti. In arte, la comprensione delle forme circolari è cruciale per la progettazione e la composizione. Anche in cucina, per calcolare le dimensioni di una torta perfetta, la circonferenza gioca un ruolo chiave!

Siamo consapevoli che la matematica può intimidire. Numeri, simboli, formule... tutto può sembrare un linguaggio alieno. Ma il nostro obiettivo è demistificare questo concetto, rendendolo accessibile e, perché no, anche un po' divertente. Prendetevi un momento. Rilassatevi. Non c'è fretta. Esploreremo insieme la formula della circonferenza, passo dopo passo.

Cos'è un cerchio? Rinfreschiamo i concetti base

Prima di immergerci nella formula, è fondamentale avere ben chiari alcuni concetti chiave:

• Cerchio: Una figura geometrica piana formata da tutti i punti equidistanti da un punto fisso, chiamato centro.
• Raggio (r): La distanza tra il centro del cerchio e un qualsiasi punto sulla circonferenza.
• Diametro (d): La distanza tra due punti sulla circonferenza che passa per il centro del cerchio. È il doppio del raggio (d = 2r).
• Circonferenza (C): La lunghezza del contorno del cerchio. È quello che stiamo cercando di calcolare!

Immagina un cerchio disegnato su un foglio di carta. Il raggio è come il raggio di una ruota di bicicletta, che va dal mozzo (il centro) al bordo. Il diametro è come una linea retta che taglia la ruota esattamente a metà, passando per il mozzo. E la circonferenza è la lunghezza di un filo che puoi far aderire perfettamente al bordo della ruota.

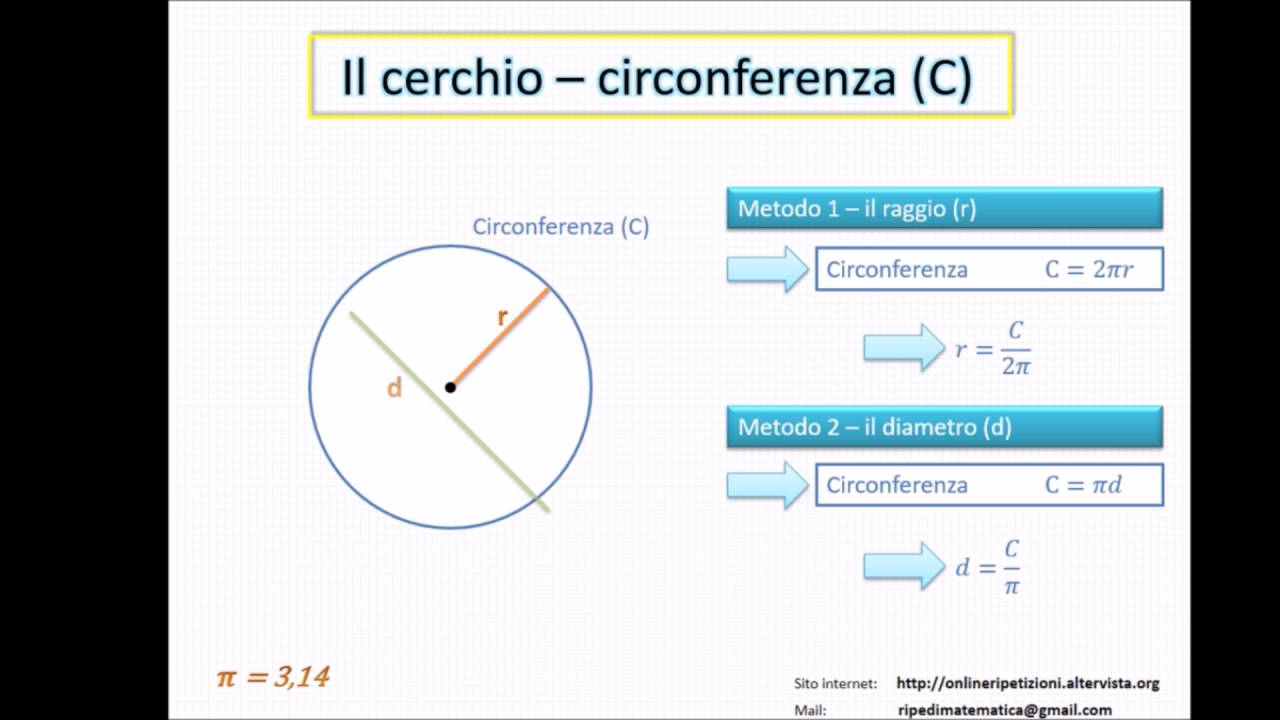
La formula magica: C = 2πr

Ecco la formula che stavi aspettando: C = 2πr

Dove:

• C rappresenta la circonferenza del cerchio.
• π (pi greco) è una costante matematica approssimativamente uguale a 3.14159 (solitamente si usa 3.14). È un numero irrazionale, il che significa che le sue cifre decimali continuano all'infinito senza ripetersi.
• r rappresenta il raggio del cerchio.

Questa formula ci dice che la circonferenza di un cerchio è semplicemente due volte pi greco moltiplicato per il suo raggio. In altre parole, se conoscessimo il raggio, potremmo sempre trovare la circonferenza.

Usando il diametro

Poiché il diametro è il doppio del raggio (d = 2r), possiamo riscrivere la formula in termini di diametro: C = πd

Questa formula è equivalente alla precedente e ci dice che la circonferenza è pi greco moltiplicato per il diametro. Scegli la formula che è più conveniente in base alle informazioni che hai a disposizione.

Esempi pratici per capire meglio

Vediamo alcuni esempi per rendere tutto più concreto:

Esempio 1: La pizza

Immagina di avere una pizza con un raggio di 15 cm. Qual è la sua circonferenza?

Usiamo la formula C = 2πr

C = 2 * 3.14 * 15 cm

C ≈ 94.2 cm

Quindi, la circonferenza della pizza è di circa 94.2 cm.

Esempio 2: La ruota di bicicletta

Una ruota di bicicletta ha un diametro di 70 cm. Qual è la sua circonferenza?

Usiamo la formula C = πd

C = 3.14 * 70 cm

C ≈ 219.8 cm

La circonferenza della ruota è di circa 219.8 cm. Questo significa che ogni volta che la ruota fa un giro completo, la bicicletta avanza di circa 219.8 cm.

Esempio 3: Il giardino circolare

Devi recintare un'aiuola circolare nel tuo giardino. Il raggio dell'aiuola è di 2 metri. Quanta recinzione ti serve?

Usiamo la formula C = 2πr

C = 2 * 3.14 * 2 metri

C ≈ 12.56 metri

Ti serviranno circa 12.56 metri di recinzione.

Affrontare le difficoltà: approssimazioni e precisione

Un aspetto importante da considerare è l'approssimazione di pi greco (π). Spesso, per semplificare i calcoli, utilizziamo 3.14. Tuttavia, pi greco è un numero irrazionale, quindi la sua rappresentazione decimale è infinita e non periodica. Questo significa che utilizzare 3.14 introduce un piccolo errore. Per calcoli che richiedono maggiore precisione, si possono utilizzare valori più accurati di pi greco o, ancora meglio, la funzione pi greco disponibile sulle calcolatrici scientifiche.

Alcune persone potrebbero chiedersi: "Ma perché usare una formula quando posso semplicemente misurare la circonferenza con un metro?" Certamente, in alcuni casi, la misurazione diretta è più semplice e veloce. Tuttavia, la formula è essenziale quando non è possibile misurare direttamente, ad esempio, quando si lavora con oggetti molto grandi (come le orbite planetarie) o molto piccoli (come le molecole). Inoltre, la formula ci fornisce una comprensione più profonda della relazione tra il raggio e la circonferenza, che è fondamentale per la risoluzione di problemi più complessi.

Oltre la formula: il significato profondo di pi greco

Pi greco è una costante universale che compare in moltissime aree della matematica e della fisica. Non si limita al cerchio, ma è presente anche in formule che descrivono onde, oscillazioni e probabilità. La sua presenza ubiquitaria sottolinea l'armonia e l'interconnessione che si trovano alla base della struttura dell'universo. Studiare la circonferenza di un cerchio, quindi, è come aprire una piccola finestra su un mondo di concetti profondi e affascinanti.

Consigli utili per memorizzare e applicare la formula

Ecco alcuni consigli per rendere la formula della circonferenza più facile da ricordare e da applicare:

• Visualizza: Immagina un cerchio e visualizza il raggio e il diametro. Collega mentalmente queste immagini alla formula.
• Pratica: Risolvi diversi esercizi. Più pratichi, più la formula diventerà automatica.
• Usa risorse online: Esistono molti siti web e app che offrono calcolatori di circonferenza e tutorial interattivi.
• Insegnare ad altri: Spiegare la formula a qualcun altro è un ottimo modo per consolidare la tua comprensione.

Ricorda, la matematica è come un muscolo: più la alleni, più diventa forte. Non scoraggiarti di fronte alle difficoltà. Sii paziente e perseverante, e alla fine sarai in grado di padroneggiare la formula della circonferenza e molti altri concetti matematici.

Conclusioni

Abbiamo esplorato la formula della circonferenza, svelandone il significato e le applicazioni pratiche. Abbiamo visto come questa semplice formula sia in realtà uno strumento potente che ci permette di comprendere e interagire con il mondo che ci circonda. Dalla pizza alla ruota di bicicletta, dal giardino circolare alle orbite planetarie, la circonferenza gioca un ruolo fondamentale.

Speriamo che questo articolo ti abbia aiutato a demistificare la formula della circonferenza e a comprenderne l'importanza. Ricorda, la matematica non è solo un insieme di regole e formule; è un linguaggio che ci permette di decifrare i segreti dell'universo.

Ora, ti invitiamo a riflettere: Dove vedi la circonferenza nella tua vita quotidiana? Come potresti utilizzare la formula che hai appena imparato per risolvere un problema pratico? Prendetevi un momento per pensare e chissà, magari la prossima volta che guarderai una pizza, la vedrai con occhi diversi!