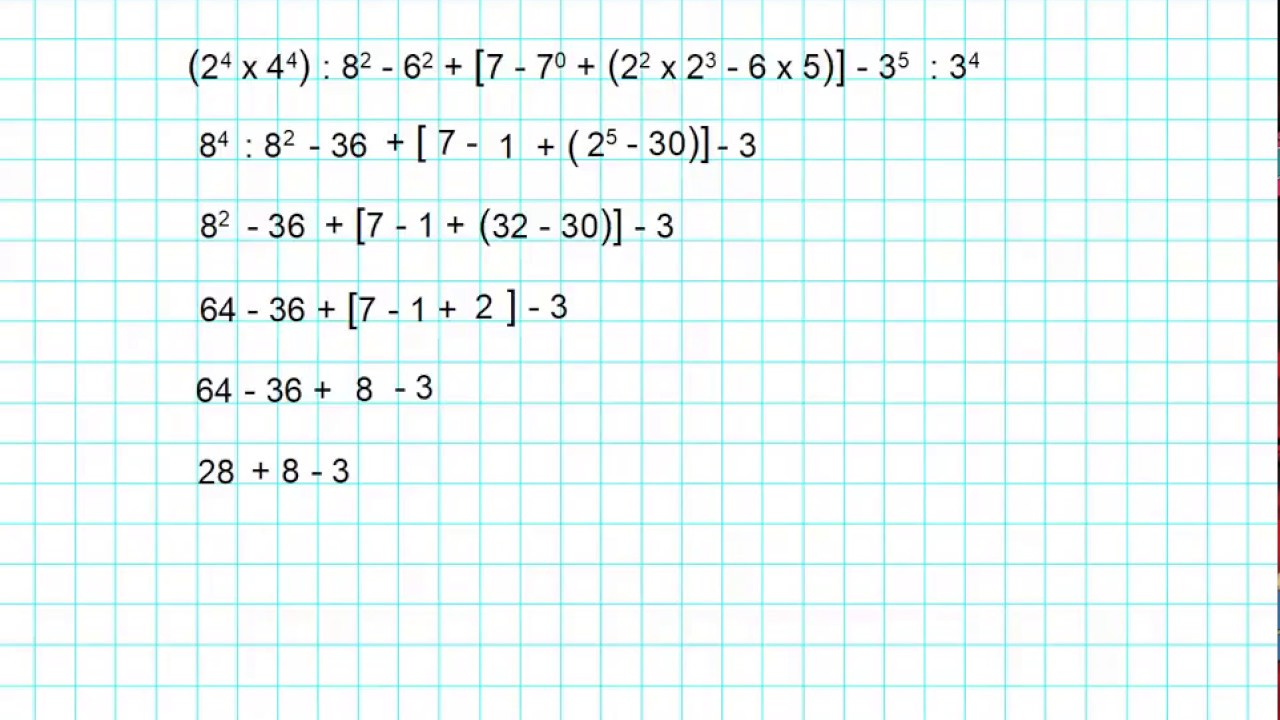Espressioni Con Potenze Esercizi Svolti Pdf

Se ti trovi qui, probabilmente stai lottando con le espressioni con potenze. Non sei solo! Molti studenti, e a volte anche adulti, si bloccano di fronte a questi esercizi. La matematica, e in particolare l'algebra, può sembrare un muro insormontabile quando non si padroneggiano le basi. Ma non temere, l'obiettivo di questo articolo è proprio quello di demistificare le espressioni con potenze, fornendo una guida chiara e completa con esercizi svolti in formato PDF da scaricare, e spiegazioni passo passo.

Perché le Espressioni con Potenze sono Importanti?

Potresti chiederti: "Ma a cosa mi servono veramente queste espressioni con potenze?". La risposta è più ampia di quanto immagini. Le potenze sono un mattoncino fondamentale in molti campi, non solo in matematica. Ecco alcuni esempi:

• Informatica: La memoria del computer, la velocità del processore, la dimensione dei file, tutto è misurato usando potenze di 2 (byte, kilobyte, megabyte, ecc.).
• Scienza: La notazione scientifica, usata per esprimere numeri molto grandi o molto piccoli (come la distanza tra le stelle o la dimensione di un atomo), si basa sulle potenze di 10.
• Finanza: Il calcolo degli interessi composti si basa sulle potenze.
• Ingegneria: La progettazione di ponti, edifici, e altre strutture richiede la comprensione delle forze, che spesso sono espresse tramite equazioni con potenze.

Quindi, capire le espressioni con potenze non è solo un esercizio accademico, ma un'abilità che ti aprirà le porte a diverse discipline e ti aiuterà a comprendere meglio il mondo che ti circonda.

Le Basi: Cosa Devi Sapere Prima di Iniziare

Prima di lanciarci negli esercizi, ripassiamo rapidamente alcuni concetti fondamentali. È cruciale avere una solida base teorica per affrontare gli esercizi con successo. Questo ti permetterà di applicare le regole correttamente e di evitare errori comuni.

Definizione di Potenza

Una potenza è un'operazione matematica che indica la moltiplicazione di un numero (la base) per se stesso un certo numero di volte (l'esponente). In altre parole:

aⁿ = a * a * a * ... * a (n volte)

Dove: * a è la base * n è l'esponente

Ad esempio: 2³ = 2 * 2 * 2 = 8

Le Proprietà delle Potenze

Le proprietà delle potenze sono delle regole che semplificano i calcoli. Conoscerle a memoria è essenziale per risolvere le espressioni in modo efficiente. Ecco le principali:

• Prodotto di potenze con la stessa base: a^m * aⁿ = a^m+n (si sommano gli esponenti)
• Quoziente di potenze con la stessa base: a^m / aⁿ = a^m-n (si sottraggono gli esponenti)
• Potenza di una potenza: (a^m)ⁿ = a^m*n (si moltiplicano gli esponenti)
• Potenza di un prodotto: (a * b)ⁿ = aⁿ * bⁿ
• Potenza di un quoziente: (a / b)ⁿ = aⁿ / bⁿ
• Potenza con esponente 0: a⁰ = 1 (con a ≠ 0)
• Potenza con esponente 1: a¹ = a
• Potenza con esponente negativo: a^-n = 1 / aⁿ

Queste regole sono il tuo arsenale. Impara ad usarle bene!

Esercizi Svolti: Guida Passo Passo

Ora passiamo alla parte pratica: gli esercizi svolti. Analizzeremo diversi esempi, di difficoltà crescente, spiegando ogni passaggio nel dettaglio. L'obiettivo è farti capire il ragionamento dietro ogni soluzione, in modo che tu possa applicarlo anche ad altri esercizi.

Esempio 1: Semplificazione di un'Espressione Semplice

Consideriamo questa espressione:

2³ * 2² / 2⁴

Passo 1: Applichiamo la proprietà del prodotto di potenze con la stessa base al numeratore:

2³⁺² / 2⁴ = 2⁵ / 2⁴

Passo 2: Applichiamo la proprietà del quoziente di potenze con la stessa base:

2^5-4 = 2¹

Passo 3: Semplicemente:

2¹ = 2

Quindi, il risultato dell'espressione è 2.

Esempio 2: Espressione con Potenza di una Potenza

Consideriamo questa espressione:

(3²)³ * 3^-1

Passo 1: Applichiamo la proprietà della potenza di una potenza:

3^2*3 * 3^-1 = 3⁶ * 3^-1

Passo 2: Applichiamo la proprietà del prodotto di potenze con la stessa base:

3^6+(-1) = 3⁵

Passo 3: Calcoliamo 3⁵:

3⁵ = 3 * 3 * 3 * 3 * 3 = 243

Quindi, il risultato dell'espressione è 243.

Esempio 3: Espressione con Numeri e Variabili

Consideriamo questa espressione:

(4x²y)² / (2xy)

Passo 1: Applichiamo la proprietà della potenza di un prodotto al numeratore:

4² * (x²)² * y² / (2xy) = 16x⁴y² / (2xy)

Passo 2: Semplifichiamo i coefficienti numerici:

16 / 2 = 8

Passo 3: Applichiamo la proprietà del quoziente di potenze con la stessa base per le variabili:

x⁴ / x = x^4-1 = x³

y² / y = y^2-1 = y¹ = y

Passo 4: Mettiamo insieme i risultati:

8x³y

Quindi, il risultato dell'espressione è 8x³y.

Errori Comuni da Evitare

Anche se conosci le regole, è facile commettere errori di distrazione. Ecco alcuni errori comuni da evitare:

• Confondere la somma con il prodotto di potenze: Ricorda, a^m + aⁿ NON si semplifica in a^m+n. Questa regola vale solo per il prodotto.
• Dimenticare l'esponente negativo: a^-n = 1 / aⁿ, non -aⁿ.
• Non applicare correttamente la proprietà della potenza di una potenza: Assicurati di moltiplicare gli esponenti, non sommarli.
• Ignorare l'ordine delle operazioni: Ricorda la gerarchia delle operazioni (parentesi, esponenti, moltiplicazioni e divisioni, addizioni e sottrazioni - PEMDAS/BODMAS).

Prestare attenzione a questi errori ti aiuterà a migliorare la tua precisione e a risolvere gli esercizi con maggiore sicurezza.

Risorse Aggiuntive: PDF con Esercizi Svolti

Per consolidare la tua comprensione e mettere alla prova le tue abilità, ho preparato un PDF scaricabile con una serie di esercizi svolti e non svolti. Questo PDF rappresenta un valido strumento per l'autoapprendimento e la preparazione a verifiche ed esami. All'interno troverai esercizi di diversa difficoltà, con soluzioni dettagliate per gli esercizi svolti e solo i risultati per quelli da provare da solo.

Questo PDF sarà disponibile a breve. Rimani sintonizzato!

Un Approccio Sistematico alla Risoluzione degli Esercizi

Ecco un approccio sistematico che puoi seguire per risolvere gli esercizi con espressioni con potenze:

1. Leggi attentamente l'espressione: Identifica le operazioni e i numeri coinvolti.
2. Individua le proprietà applicabili: Cerca le combinazioni di termini che ti permettono di applicare le proprietà delle potenze.
3. Applica le proprietà passo dopo passo: Sii metodico e scrivi ogni passaggio in modo chiaro.
4. Semplifica l'espressione: Riduci l'espressione al minimo termine.
5. Controlla il risultato: Verifica se il risultato è ragionevole e se hai applicato correttamente le regole.

Seguire questo approccio ti aiuterà a evitare errori e a risolvere gli esercizi in modo più efficiente.

Un Passo Indietro: Quando Serve Rivedere le Basi

Se, nonostante tutti questi consigli ed esempi, ti trovi ancora in difficoltà, forse è il momento di fare un passo indietro e rivedere le basi dell'algebra. A volte, la difficoltà non è tanto nelle potenze in sé, quanto nella mancanza di una solida base teorica. Riconsidera argomenti come:

• Operazioni con i numeri relativi
• Semplificazione di espressioni algebriche
• Frazioni algebriche
• Equazioni di primo grado

Rafforzare queste basi ti renderà più facile affrontare anche le espressioni con potenze.

Oltre gli Esercizi: Approfondimenti Utili

Per approfondire ulteriormente l'argomento, puoi consultare diverse risorse online e offline. Esistono numerosi siti web, video tutorial e libri di testo che spiegano le espressioni con potenze in modo chiaro e completo. Inoltre, puoi chiedere aiuto al tuo insegnante o a un tutor di matematica.

Non aver paura di chiedere aiuto! Imparare è un processo continuo e collaborativo.

Spero che questo articolo ti sia stato utile per capire meglio le espressioni con potenze e per affrontare gli esercizi con maggiore sicurezza. Ricorda, la pratica è fondamentale. Più ti eserciti, più diventerai bravo!

Ora, prova a mettere in pratica quello che hai imparato. Quale strategia useresti per risolvere un'espressione complessa con diverse operazioni e potenze?