Espressioni Con Numeri Relativi Frazioni E Potenze Pdf

Le espressioni numeriche, in matematica, rappresentano un pilastro fondamentale per la comprensione e la manipolazione dei numeri. Quando queste espressioni includono numeri relativi, frazioni e potenze, il livello di complessità aumenta, richiedendo una solida base di conoscenze e una rigorosa applicazione delle regole algebriche. Questo articolo esplorerà in dettaglio le espressioni con numeri relativi, frazioni e potenze, fornendo una guida completa e chiara per la loro risoluzione.

Numeri Relativi: Un'Introduzione

I numeri relativi comprendono sia i numeri positivi che i numeri negativi, inclusi lo zero. L'operazione con numeri relativi richiede una comprensione accurata delle regole dei segni. Ad esempio, la somma di due numeri negativi darà un numero negativo, mentre la somma di un numero positivo e uno negativo dipenderà dal valore assoluto dei numeri.

Regole Fondamentali per i Numeri Relativi

Le regole fondamentali per operare con i numeri relativi sono:

Somma: Se i segni sono uguali, si sommano i valori assoluti e si mantiene il segno comune. Se i segni sono diversi, si sottrae il valore assoluto minore dal maggiore e si mette il segno del numero con il valore assoluto maggiore.
Sottrazione: Sottraendo un numero relativo, equivale ad aggiungere il suo opposto. Ad esempio, a - (-b) = a + b.
Moltiplicazione e Divisione: Se i segni sono uguali, il risultato è positivo. Se i segni sono diversi, il risultato è negativo.

Queste regole sono cruciali per la corretta risoluzione delle espressioni che coinvolgono numeri relativi.

Frazioni: Operazioni e Semplificazioni

Le frazioni rappresentano una parte di un intero e sono composte da un numeratore (il numero sopra la linea di frazione) e un denominatore (il numero sotto la linea di frazione). Operare con le frazioni richiede di saper trovare il minimo comune multiplo (m.c.m.) e semplificare le frazioni ai minimi termini.

Operazioni con le Frazioni

Le principali operazioni con le frazioni includono:

Addizione e Sottrazione: Per sommare o sottrarre frazioni, è necessario che abbiano lo stesso denominatore. Se i denominatori sono diversi, si deve trovare il m.c.m. dei denominatori e trasformare le frazioni in frazioni equivalenti con il denominatore comune.
Moltiplicazione: Per moltiplicare due frazioni, si moltiplicano i numeratori tra loro e i denominatori tra loro.
Divisione: Per dividere due frazioni, si moltiplica la prima frazione per l'inverso della seconda frazione.

Esempio: Consideriamo l'espressione (1/2 + 1/3) * (2/5). Prima, sommiamo 1/2 e 1/3. Il m.c.m. di 2 e 3 è 6. Quindi, 1/2 diventa 3/6 e 1/3 diventa 2/6. La somma è 3/6 + 2/6 = 5/6. Ora moltiplichiamo 5/6 per 2/5, ottenendo (5*2)/(6*5) = 10/30. Semplificando, otteniamo 1/3.

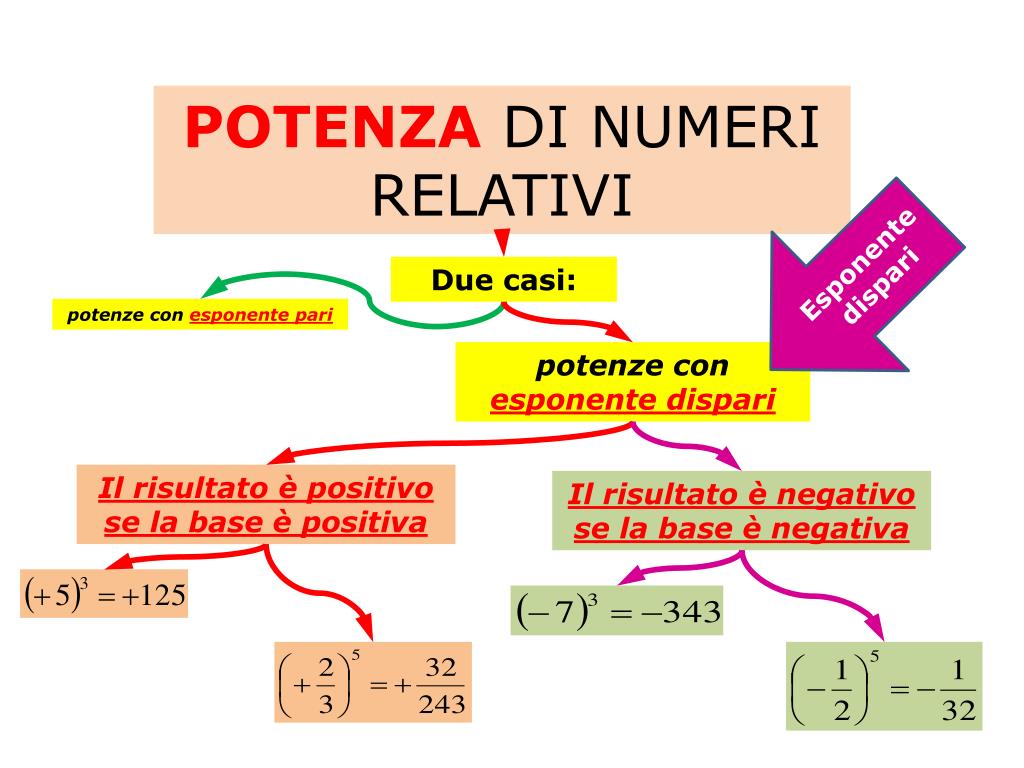
Potenze: Definizioni e Proprietà

La potenza rappresenta un'operazione matematica che indica la moltiplicazione ripetuta di un numero per se stesso. Un numero (la base) viene elevato a un esponente. Le potenze con esponente intero positivo sono le più semplici, ma le potenze possono avere anche esponenti negativi o frazionari.

Proprietà delle Potenze

Le proprietà fondamentali delle potenze includono:

Prodotto di potenze con la stessa base: a^m * aⁿ = a^m+n
Quoziente di potenze con la stessa base: a^m / aⁿ = a^m-n
Potenza di una potenza: (a^m)ⁿ = a^m*n
Potenza con esponente negativo: a^-n = 1/aⁿ
Potenza con esponente zero: a⁰ = 1 (con a ≠ 0)

Esempio: Consideriamo l'espressione (2³ * 2^-1) / 2². Usando la proprietà del prodotto di potenze con la stessa base, 2³ * 2^-1 = 2^3+(-1) = 2². Quindi, l'espressione diventa 2² / 2². Usando la proprietà del quoziente di potenze con la stessa base, 2² / 2² = 2^2-2 = 2⁰ = 1.

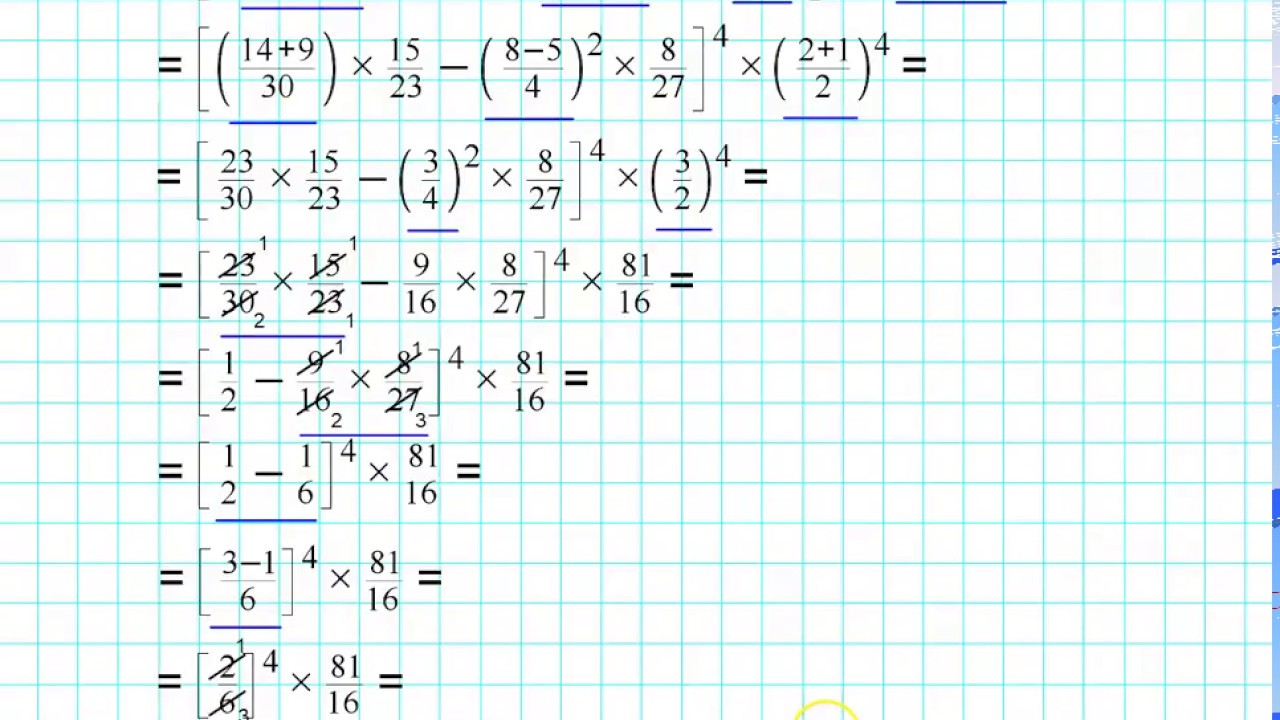
Espressioni Complesse: Ordine delle Operazioni e Priorità

Quando si affrontano espressioni complesse che coinvolgono numeri relativi, frazioni e potenze, è fondamentale seguire l'ordine delle operazioni, spesso ricordato con l'acronimo PEMDAS (Parentesi, Esponenti, Moltiplicazioni e Divisioni, Addizioni e Sottrazioni).

Passi per Risolvere Espressioni Complesse

Parentesi: Risolvere le operazioni all'interno delle parentesi, seguendo l'ordine delle operazioni all'interno delle parentesi stesse.
Esponenti: Calcolare le potenze.
Moltiplicazioni e Divisioni: Eseguire moltiplicazioni e divisioni da sinistra a destra.
Addizioni e Sottrazioni: Eseguire addizioni e sottrazioni da sinistra a destra.

Esempio: Consideriamo l'espressione ( -2 + 1/2 )² * ( 3/4 - 1 ). Prima, risolviamo la parentesi ( -2 + 1/2 ). Convertiamo -2 in -4/2, quindi abbiamo -4/2 + 1/2 = -3/2. Ora, risolviamo l'altra parentesi ( 3/4 - 1 ). Convertiamo 1 in 4/4, quindi abbiamo 3/4 - 4/4 = -1/4. Ora eleviamo -3/2 al quadrato: (-3/2)² = 9/4. Infine, moltiplichiamo 9/4 per -1/4: (9/4) * (-1/4) = -9/16.

Esempi Pratici e Applicazioni Reali

Le espressioni con numeri relativi, frazioni e potenze non sono solo un esercizio matematico astratto, ma trovano applicazione in numerosi campi della vita reale.

Finanza: Calcolo degli interessi composti (che coinvolgono potenze) e gestione dei debiti (che coinvolgono numeri relativi). Ad esempio, il calcolo degli interessi su un mutuo o un prestito spesso utilizza espressioni complesse con potenze e frazioni.
Scienza: Misurazioni scientifiche, calcoli di concentrazioni chimiche (che utilizzano frazioni) e modellizzazione di fenomeni fisici (che spesso coinvolgono potenze). La legge di gravitazione universale di Newton, ad esempio, include una relazione inversamente proporzionale al quadrato della distanza (una potenza con esponente -2).
Ingegneria: Progettazione di strutture, calcolo di carichi e tensioni (che spesso coinvolgono numeri relativi e frazioni) e analisi di circuiti elettrici (che utilizzano numeri complessi e potenze).
Informatica: Algoritmi e programmazione, dove la gestione dei dati e la manipolazione di variabili richiedono la comprensione e l'applicazione di numeri relativi, frazioni e potenze. La rappresentazione di numeri in formato binario e le operazioni su di essi utilizzano ampiamente le potenze di 2.

Esempio Finanziario: Supponiamo di investire 1000€ con un interesse annuo del 5% composto trimestralmente. Dopo 5 anni, quanto avremo? La formula è: A = P(1 + r/n)^nt, dove A è l'ammontare finale, P è il capitale iniziale (1000€), r è il tasso di interesse annuo (0.05), n è il numero di volte che l'interesse è composto all'anno (4), e t è il numero di anni (5). Quindi, A = 1000(1 + 0.05/4)^4*5 = 1000(1.0125)²⁰ ≈ 1282.04€. Questo calcolo richiede la comprensione e l'applicazione di potenze e frazioni.

Errori Comuni e Come Evitarli

Nella risoluzione di espressioni con numeri relativi, frazioni e potenze, è facile commettere errori. Alcuni errori comuni includono:

Errori di segno: Confondere i segni positivi e negativi durante le operazioni con i numeri relativi.
Errori nella semplificazione delle frazioni: Dimenticare di semplificare le frazioni ai minimi termini.
Errori nell'applicazione delle proprietà delle potenze: Applicare erroneamente le regole per il prodotto, il quoziente o la potenza di una potenza.
Errori nell'ordine delle operazioni: Non seguire l'ordine corretto delle operazioni (PEMDAS).

Per evitare questi errori, è consigliabile:

Rivedere le regole fondamentali: Assicurarsi di comprendere e ricordare le regole dei segni, le operazioni con le frazioni e le proprietà delle potenze.
Lavorare passo dopo passo: Risolvere le espressioni passo dopo passo, scrivendo chiaramente ogni passaggio.
Verificare i risultati: Controllare attentamente i risultati di ogni passaggio per individuare eventuali errori.
Esercitarsi regolarmente: La pratica costante aiuta a consolidare le conoscenze e a migliorare la precisione.

Conclusioni

Le espressioni con numeri relativi, frazioni e potenze rappresentano una sfida importante nella matematica, ma con una solida comprensione delle regole e una pratica costante, è possibile superare questa sfida con successo. Ricordate l'importanza dell'ordine delle operazioni, la corretta applicazione delle proprietà delle potenze e la cura nella manipolazione delle frazioni. Utilizzate le risorse disponibili, come libri di testo, esercizi online e guide pratiche, per approfondire le vostre conoscenze. La padronanza di queste competenze vi aprirà le porte a una comprensione più profonda della matematica e delle sue applicazioni nel mondo reale. Non abbiate paura di affrontare problemi complessi; ogni errore è un'opportunità per imparare e crescere.