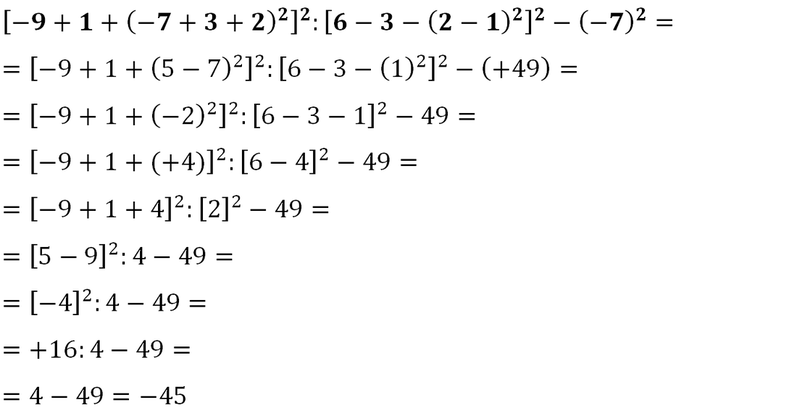Espressioni Con Numeri Relativi E Potenze Esercizi

Ciao! Ti sei mai trovato di fronte a un'espressione matematica che sembrava un vero e proprio labirinto, piena di numeri relativi e potenze? Tranquillo, non sei solo! Molti studenti, e a volte anche qualche adulto, si sentono sopraffatti da questo tipo di esercizi. La buona notizia è che, con la giusta guida e un po' di pratica, questi problemi possono diventare molto più accessibili e persino divertenti. In questo articolo, ti accompagnerò passo dopo passo attraverso le insidie delle espressioni con numeri relativi e potenze, offrendoti esempi pratici, consigli utili e, soprattutto, un approccio chiaro e semplificato.

Immagina di dover gestire un budget personale dove hai entrate (numeri positivi) e spese (numeri negativi). A volte devi raddoppiare le tue entrate (potenza), altre volte devi dividere equamente le spese (divisione). Capire come operare con numeri positivi, negativi e potenze ti aiuta a gestire meglio le tue finanze. Allo stesso modo, queste competenze sono fondamentali in molti altri campi, dalla fisica all'informatica, rendendo cruciale la loro padronanza.

Numeri Relativi: Amici e Nemici

Partiamo dalle basi: i numeri relativi sono semplicemente numeri con un segno, positivo (+) o negativo (-). I numeri positivi sono quelli che usiamo normalmente per contare, mentre i numeri negativi rappresentano l'opposto (debiti, temperature sotto lo zero, ecc.).

Operazioni con i numeri relativi:

• Addizione:
  • Se i numeri hanno lo stesso segno, si sommano i valori assoluti e si mantiene il segno comune. Esempio: (+3) + (+5) = +8; (-2) + (-4) = -6
  • Se i numeri hanno segni diversi, si sottrae il valore assoluto minore dal valore assoluto maggiore e si mantiene il segno del numero con il valore assoluto maggiore. Esempio: (+7) + (-3) = +4; (-9) + (+2) = -7
• Sottrazione: La sottrazione di un numero relativo è equivalente all'addizione del suo opposto. Esempio: (+5) - (+2) = (+5) + (-2) = +3; (-3) - (-1) = (-3) + (+1) = -2
• Moltiplicazione e Divisione:
  • Se i numeri hanno lo stesso segno, il risultato è positivo. Esempio: (+2) * (+3) = +6; (-4) * (-2) = +8; (+6) / (+2) = +3; (-8) / (-4) = +2
  • Se i numeri hanno segni diversi, il risultato è negativo. Esempio: (+5) * (-1) = -5; (-3) * (+4) = -12; (+9) / (-3) = -3; (-10) / (+2) = -5

Ricorda la regolina dei segni: più per più fa più, meno per meno fa più, più per meno fa meno, meno per più fa meno. Questa regolina è valida sia per la moltiplicazione che per la divisione.

Potenze: Moltiplicazione Iterata

Una potenza è un modo compatto per scrivere una moltiplicazione ripetuta dello stesso numero. Ad esempio, 2³ significa 2 * 2 * 2 = 8. Il numero 2 è la base, mentre il numero 3 è l'esponente.

Regole delle potenze:

• Potenza con esponente positivo intero: aⁿ = a * a * ... * a (n volte)
• Potenza con esponente zero: a⁰ = 1 (a ≠ 0). Qualsiasi numero elevato a zero fa 1.
• Potenza con esponente negativo intero: a^-n = 1 / aⁿ (a ≠ 0). Un esponente negativo indica l'inverso della potenza con esponente positivo. Esempio: 2^-3 = 1 / 2³ = 1 / 8
• Prodotto di potenze con la stessa base: a^m * aⁿ = a^m+n. Quando moltiplichi potenze con la stessa base, sommi gli esponenti. Esempio: 2² * 2³ = 2⁵ = 32
• Quoziente di potenze con la stessa base: a^m / aⁿ = a^m-n. Quando dividi potenze con la stessa base, sottrai gli esponenti. Esempio: 2⁵ / 2² = 2³ = 8
• Potenza di una potenza: (a^m)ⁿ = a^m*n. Quando elevi una potenza a un'altra potenza, moltiplichi gli esponenti. Esempio: (2²)³ = 2⁶ = 64

Attenzione ai segni!

Quando la base è negativa, il segno del risultato dipende dall'esponente:

• Se l'esponente è pari, il risultato è positivo. Esempio: (-2)² = 4; (-3)⁴ = 81
• Se l'esponente è dispari, il risultato è negativo. Esempio: (-2)³ = -8; (-3)³ = -27

Espressioni: L'Ordine è Fondamentale

Ora che abbiamo ripassato i numeri relativi e le potenze, possiamo affrontare le espressioni. La chiave per risolvere correttamente un'espressione è seguire l'ordine delle operazioni, noto anche come PEMDAS o BODMAS:

1. Parentesi (o Brackets) - Risolvi prima le operazioni all'interno delle parentesi (tonde, quadre, graffe), partendo dalle più interne.
2. Esponenti (o Orders) - Calcola le potenze e le radici.
3. Moltiplicazione e Divisione - Esegui moltiplicazioni e divisioni nell'ordine in cui compaiono, da sinistra a destra.
4. Addizione e Sottrazione - Esegui addizioni e sottrazioni nell'ordine in cui compaiono, da sinistra a destra.

Un trucco mnemonico per ricordare l'ordine è: Prima le Parentesi, poi le Potenze, Moltiplicazioni e Divisioni, infine Addizioni e Sottrazioni. "PP Mi Divano A Sbagliare"

Esempio Pratico: Un'Espressione da Decifrare

Consideriamo la seguente espressione:

(-2)³ + 3 * (-4 + 1) - 5 / (-1)

1. Parentesi: Risolviamo prima l'operazione all'interno delle parentesi tonde: (-4 + 1) = -3
2. Esponenti: Calcoliamo la potenza: (-2)³ = -8
3. Moltiplicazione e Divisione: Eseguiamo la moltiplicazione e la divisione: 3 * (-3) = -9; 5 / (-1) = -5
4. Addizione e Sottrazione: Infine, eseguiamo le addizioni e le sottrazioni: -8 + (-9) - (-5) = -8 - 9 + 5 = -12

Quindi, il risultato dell'espressione è -12.

Esercizi Proposti (con Soluzioni Nascoste!):

Metti alla prova le tue abilità con questi esercizi. Ricorda di seguire l'ordine delle operazioni e di fare attenzione ai segni!

1. 5 + (-3) * 2² - 10 / (-2)
2. (4 - 7) * (-1)⁵ + 6 / 3
3. -2 * (3 + 2³) - (-5)²
4. 12 / (-4) + 8 * (-1)² - 6
5. (-3)² - 4 * (2 - 5) + 1

Errori Comuni da Evitare

Ecco alcuni errori comuni che è bene evitare quando si risolvono espressioni con numeri relativi e potenze:

• Dimenticare l'ordine delle operazioni: Questo è l'errore più comune. Assicurati di seguire sempre PEMDAS/BODMAS.
• Confondere i segni: Presta molta attenzione ai segni positivi e negativi, soprattutto durante la moltiplicazione e la divisione.
• Applicare male le regole delle potenze: Ricorda le regole per il prodotto, il quoziente e la potenza di una potenza.
• Trascurare le parentesi: Le parentesi indicano l'ordine in cui devono essere eseguite le operazioni. Non ignorarle!
• Non semplificare prima di calcolare: Se possibile, semplifica l'espressione prima di iniziare a calcolare. Questo può ridurre il rischio di errori.

Un Ultimo Consiglio: Pratica, Pratica, Pratica!

Come per qualsiasi altra abilità, la pratica è fondamentale per padroneggiare le espressioni con numeri relativi e potenze. Risolvi quanti più esercizi possibile, partendo da quelli più semplici e aumentando gradualmente la difficoltà. Non aver paura di commettere errori; gli errori sono un'opportunità per imparare e migliorare. Se hai difficoltà, chiedi aiuto al tuo insegnante, a un tutor o a un compagno di classe. Ci sono anche molte risorse online, come video tutorial ed esercizi interattivi, che possono esserti utili.

Alcuni studenti considerano le espressioni un ostacolo insormontabile, mentre altri le vedono come un puzzle stimolante da risolvere. La verità è che, con un approccio metodico e una buona dose di perseveranza, chiunque può imparare a gestire queste espressioni con sicurezza e successo. Non scoraggiarti di fronte alle difficoltà, ma affrontale con curiosità e determinazione. Ricorda che ogni esercizio risolto è un passo avanti verso la padronanza della matematica.

Ora, ripensa a quando hai iniziato a leggere questo articolo. Ti sentivi forse un po' intimidito dalle espressioni con numeri relativi e potenze? Spero che, dopo aver letto le spiegazioni, gli esempi e i consigli che ti ho offerto, tu ti senta più sicuro e preparato ad affrontare queste sfide matematiche. Ricorda: la matematica non è una materia da temere, ma un linguaggio potente che può aprirti le porte a infinite possibilità. Prova a risolvere gli esercizi proposti e, soprattutto, non smettere mai di imparare e di sperimentare.

Qual è il prossimo esercizio che ti metterà alla prova?