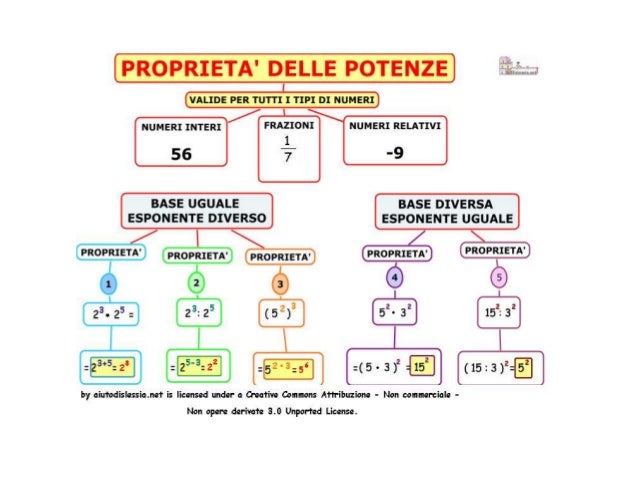
Espressioni Con Le Proprietà Delle Potenze

Sei mai rimasto bloccato davanti a un'espressione matematica apparentemente impossibile da risolvere, piena di numeri con esponenti strani? Non preoccuparti, capita a tutti! Questo articolo è pensato per te, studente delle scuole medie o superiori, o per chiunque voglia rinfrescare le proprie conoscenze di matematica. Ti guideremo attraverso il mondo delle espressioni con le proprietà delle potenze, rendendole chiare, accessibili e, perché no, anche un po' divertenti.

Un Viaggio nel Mondo delle Potenze

Prima di tuffarci nelle espressioni, cerchiamo di capire cos'è una potenza. In termini semplici, una potenza è un modo abbreviato di scrivere una moltiplicazione ripetuta. Ad esempio, 2³ (letto "due alla terza") significa 2 * 2 * 2 = 8. Qui, 2 è la base e 3 è l'esponente.

Ma perché impazzire con le potenze? Beh, le potenze sono ovunque, dalla scienza all'informatica, e sono essenziali per descrivere fenomeni che crescono o decrescono molto rapidamente. Pensa alla crescita batterica, al calcolo degli interessi composti o alla dimensione dei dati digitali.

Le Magiche Proprietà delle Potenze

Il bello delle potenze è che seguono delle regole precise, le cosiddette proprietà, che ci permettono di semplificare le espressioni e renderle più facili da risolvere. Vediamo le principali:

1. Prodotto di potenze con la stessa base

Quando moltiplichiamo due potenze che hanno la stessa base, sommiamo gli esponenti. In formula: a^m * aⁿ = a^m+n.

Esempio: 2³ * 2² = 2³⁺² = 2⁵ = 32. Verifichiamo: 2³ = 8, 2² = 4, e 8 * 4 = 32. Funziona!

Perché funziona? Perché stiamo semplicemente combinando le moltiplicazioni ripetute. a^m significa "a moltiplicato per se stesso m volte", e aⁿ significa "a moltiplicato per se stesso n volte". Quindi, moltiplicando a^m e aⁿ, stiamo moltiplicando "a" per se stesso (m+n) volte.

2. Quoziente di potenze con la stessa base

Quando dividiamo due potenze che hanno la stessa base, sottraiamo gli esponenti. In formula: a^m / aⁿ = a^m-n (con a ≠ 0).

Esempio: 3⁵ / 3² = 3^5-2 = 3³ = 27. Verifichiamo: 3⁵ = 243, 3² = 9, e 243 / 9 = 27.

Perché funziona? Simile al prodotto, stiamo "cancellando" le moltiplicazioni ripetute. Se abbiamo "a" moltiplicato per se stesso 5 volte, e lo dividiamo per "a" moltiplicato per se stesso 2 volte, rimaniamo con "a" moltiplicato per se stesso 3 volte.

3. Potenza di una potenza

Quando eleviamo una potenza a un altro esponente, moltiplichiamo gli esponenti. In formula: (a^m)ⁿ = a^m*n.

Esempio: (2²)³ = 2^2*3 = 2⁶ = 64. Verifichiamo: 2² = 4, e 4³ = 4 * 4 * 4 = 64.

Perché funziona? (a^m)ⁿ significa "a^m moltiplicato per se stesso n volte". Ogni a^m è "a moltiplicato per se stesso m volte". Quindi, in totale, stiamo moltiplicando "a" per se stesso m*n volte.

4. Potenza di un prodotto

Quando eleviamo un prodotto a un esponente, eleviamo ogni fattore del prodotto a quell'esponente. In formula: (a * b)ⁿ = aⁿ * bⁿ.

Esempio: (2 * 3)² = 2² * 3² = 4 * 9 = 36. Verifichiamo: 2 * 3 = 6, e 6² = 36.

Perché funziona? (a * b)ⁿ significa (a * b) moltiplicato per se stesso n volte: (a * b) * (a * b) * ... * (a * b) (n volte). Possiamo riorganizzare i fattori per ottenere a * a * ... * a (n volte) * b * b * ... * b (n volte), che è esattamente aⁿ * bⁿ.

5. Potenza di un quoziente

Quando eleviamo un quoziente a un esponente, eleviamo sia il numeratore che il denominatore a quell'esponente. In formula: (a / b)ⁿ = aⁿ / bⁿ (con b ≠ 0).

Esempio: (4 / 2)³ = 4³ / 2³ = 64 / 8 = 8. Verifichiamo: 4 / 2 = 2, e 2³ = 8.

Perché funziona? Simile al prodotto, stiamo elevando sia il numeratore che il denominatore alla potenza "n".

6. Esponente zero

Qualsiasi numero (diverso da zero) elevato a 0 è uguale a 1. In formula: a⁰ = 1 (con a ≠ 0).

Esempio: 5⁰ = 1, 100⁰ = 1, (-3)⁰ = 1.

Perché funziona? Possiamo vederlo come un caso speciale della proprietà del quoziente. Considera aⁿ / aⁿ. Sappiamo che qualsiasi numero (diverso da zero) diviso per se stesso è uguale a 1. Ma, usando la proprietà del quoziente, aⁿ / aⁿ = a^n-n = a⁰. Quindi, a⁰ deve essere uguale a 1.

7. Esponente negativo

Un numero elevato a un esponente negativo è uguale all'inverso del numero elevato all'esponente positivo. In formula: a^-n = 1 / aⁿ (con a ≠ 0).

Esempio: 2^-3 = 1 / 2³ = 1 / 8.

Perché funziona? Possiamo pensare a questo come un'estensione della proprietà del quoziente. Considera a⁰ / aⁿ. Sappiamo che a⁰ = 1. Quindi, a⁰ / aⁿ = 1 / aⁿ. Ma, usando la proprietà del quoziente, a⁰ / aⁿ = a^0-n = a^-n. Quindi, a^-n deve essere uguale a 1 / aⁿ.

Mettiamoci alla Prova: Risolvere le Espressioni

Ora che conosciamo le proprietà, vediamo come applicarle per semplificare e risolvere espressioni complesse.

Esempio 1: (2³ * 2^-1) / 2²

• Applichiamo la proprietà del prodotto al numeratore: 2³ * 2^-1 = 2^{3 + (-1)} = 2²
• Ora abbiamo: 2² / 2²
• Applichiamo la proprietà del quoziente: 2² / 2² = 2^2-2 = 2⁰
• Infine, applichiamo la proprietà dell'esponente zero: 2⁰ = 1
• Quindi, (2³ * 2^-1) / 2² = 1

Esempio 2: (3²)³ * 3^-4

• Applichiamo la proprietà della potenza di una potenza: (3²)³ = 3^2*3 = 3⁶
• Ora abbiamo: 3⁶ * 3^-4
• Applichiamo la proprietà del prodotto: 3⁶ * 3^-4 = 3^{6 + (-4)} = 3²
• Infine: 3² = 9
• Quindi, (3²)³ * 3^-4 = 9

Esempio 3: (5 * 2)² / 5²

• Applichiamo la proprietà della potenza di un prodotto: (5 * 2)² = 5² * 2²
• Ora abbiamo: (5² * 2²) / 5²
• Possiamo semplificare dividendo 5² per 5², che dà 1: 1 * 2² = 2²
• Infine: 2² = 4
• Quindi, (5 * 2)² / 5² = 4

Consigli Utili per Diventare un Maestro delle Potenze

• Familiarizza con le proprietà: Più le pratichi, più diventeranno naturali.
• Scomponi i numeri: Se l'espressione contiene numeri grandi, prova a scomporli in fattori primi. Questo può aiutarti a identificare le basi comuni.
• Scrivi tutti i passaggi: All'inizio, scrivi ogni singolo passaggio per evitare errori.
• Verifica le risposte: Se hai tempo, verifica le tue risposte sostituendo i risultati nell'espressione originale.
• Non aver paura di chiedere aiuto: Se ti blocchi, chiedi aiuto a un insegnante, a un compagno di classe o consulta risorse online.

Un Ultimo Pensiero

Le espressioni con le proprietà delle potenze possono sembrare spaventose all'inizio, ma con la pratica e la comprensione delle regole di base, diventeranno un gioco da ragazzi. Ricorda, la matematica è un linguaggio, e le potenze sono solo una parte di questo linguaggio. Impara a parlarlo fluentemente, e aprirai un mondo di possibilità!

Speriamo che questo articolo ti sia stato utile. Ora tocca a te! Prendi carta e penna, esercitati con diversi esempi, e scopri la potenza delle potenze! Buon divertimento!