Espressioni Con Le 4 Operazioni

Benvenuti nel regno affascinante e rigoroso delle espressioni con le quattro operazioni fondamentali: addizione, sottrazione, moltiplicazione e divisione. Qui, l'aritmetica non è semplice calcolo, ma un linguaggio preciso, una grammatica di numeri e simboli che, se interpretata correttamente, rivela soluzioni inequivocabili. Prepariamoci ad un'immersione profonda, armati di precisione e metodo, per navigare con sicurezza tra parentesi, precedenze e strategie risolutive.

Le espressioni aritmetiche rappresentano la colonna vertebrale della matematica elementare e superiore. Comprendere la loro struttura e il loro funzionamento è cruciale per costruire solide fondamenta in ogni disciplina scientifica. Iniziamo quindi a smontare i meccanismi che governano queste entità matematiche, analizzando le regole di precedenza e le tecniche di semplificazione più efficaci.

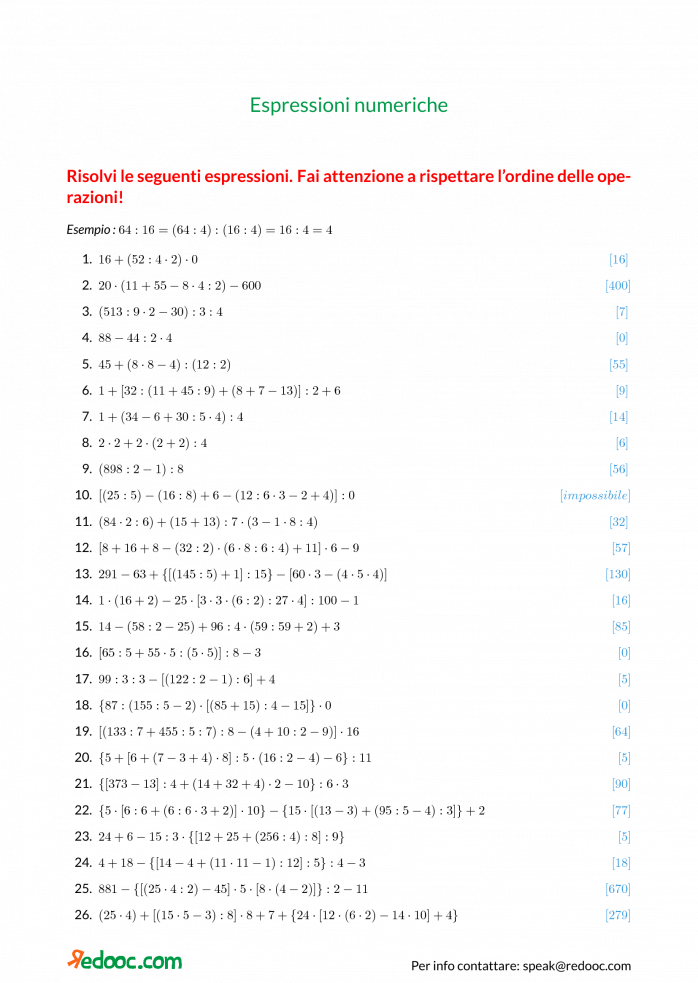
L'ordine delle operazioni è la pietra angolare per la corretta risoluzione di qualsiasi espressione. Ricordate sempre l'acronimo PEMDAS o, nella sua versione italiana, PAMDAS:

• Parentesi (o altre notazioni di raggruppamento: parentesi quadre e graffe)
• Addizione e Sottrazione (eseguite da sinistra a destra, nello stesso ordine in cui compaiono)
• Moltiplicazione e Divisione (eseguite da sinistra a destra, nello stesso ordine in cui compaiono)

Ignorare questo ordine fondamentale porterà inevitabilmente a risultati errati. La matematica, in questo senso, è inflessibile: la precisione è il suo pane quotidiano.

Esempi di Risoluzione Passo Passo

Analizziamo alcuni esempi concreti per illustrare l'applicazione pratica del PAMDAS.

Consideriamo l'espressione: 12 + 3 * 4 - 8 / 2.

1. Moltiplicazione e Divisione: Eseguiamo prima la moltiplicazione e la divisione da sinistra a destra. 3 * 4 = 12 e 8 / 2 = 4. L'espressione diventa: 12 + 12 - 4.

2. Addizione e Sottrazione: Ora eseguiamo l'addizione e la sottrazione da sinistra a destra. 12 + 12 = 24. L'espressione diventa: 24 - 4.

3. Risultato Finale: Infine, 24 - 4 = 20. Il risultato dell'espressione è 20.

Esaminiamo un esempio con parentesi: (5 + 3) * 2 - 10 / 5.

1. Parentesi: Calcoliamo prima il contenuto delle parentesi: 5 + 3 = 8. L'espressione diventa: 8 * 2 - 10 / 5.

2. Moltiplicazione e Divisione: Eseguiamo la moltiplicazione e la divisione da sinistra a destra: 8 * 2 = 16 e 10 / 5 = 2. L'espressione diventa: 16 - 2.

3. Sottrazione: Infine, 16 - 2 = 14. Il risultato dell'espressione è 14.

Un esempio più complesso con parentesi annidate: [4 + (6 - 2) * 3] / 2.

1. Parentesi Interne: Iniziamo con le parentesi più interne: 6 - 2 = 4. L'espressione diventa: [4 + 4 * 3] / 2.

2. Moltiplicazione all'Interno delle Parentesi Quadre: Eseguiamo la moltiplicazione all'interno delle parentesi quadre: 4 * 3 = 12. L'espressione diventa: [4 + 12] / 2.

3. Somma all'Interno delle Parentesi Quadre: Calcoliamo la somma all'interno delle parentesi quadre: 4 + 12 = 16. L'espressione diventa: 16 / 2.

4. Divisione: Infine, eseguiamo la divisione: 16 / 2 = 8. Il risultato dell'espressione è 8.

Questi esempi dimostrano l'importanza di seguire rigorosamente l'ordine delle operazioni. La precisione è fondamentale per ottenere il risultato corretto.

Strategie Avanzate per la Semplificazione

Oltre all'ordine delle operazioni, esistono diverse strategie che possono semplificare la risoluzione di espressioni complesse. Una di queste è l'uso delle proprietà delle operazioni.

• Proprietà Commutativa: Questa proprietà afferma che l'ordine degli addendi in una somma (o dei fattori in una moltiplicazione) non cambia il risultato. Ad esempio, a + b = b + a e a * b = b * a.

• Proprietà Associativa: Questa proprietà afferma che il modo in cui raggruppiamo gli addendi in una somma (o i fattori in una moltiplicazione) non cambia il risultato. Ad esempio, (a + b) + c = a + (b + c) e (a * b) * c = a * (b * c).

• Proprietà Distributiva: Questa proprietà è fondamentale per semplificare espressioni che coinvolgono sia la moltiplicazione che l'addizione (o la sottrazione). Afferma che a * (b + c) = a * b + a * c.

Queste proprietà, se applicate correttamente, possono ridurre la complessità delle espressioni e facilitare il calcolo.

Esempio di Applicazione delle Proprietà:

Consideriamo l'espressione: 5 * (12 + 8).

1. Utilizzando la Proprietà Distributiva: Possiamo riscrivere l'espressione come: 5 * 12 + 5 * 8.

2. Calcolo delle Moltiplicazioni: 5 * 12 = 60 e 5 * 8 = 40. L'espressione diventa: 60 + 40.

3. Addizione: 60 + 40 = 100.

Alternativamente, avremmo potuto risolvere l'espressione seguendo l'ordine delle operazioni:

1. Parentesi: 12 + 8 = 20. L'espressione diventa: 5 * 20.

2. Moltiplicazione: 5 * 20 = 100.

In questo caso, entrambe le strade portano allo stesso risultato. Tuttavia, in espressioni più complesse, l'applicazione delle proprietà può semplificare notevolmente il processo di calcolo.

Un'altra strategia utile è la fattorizzazione. Se in un'espressione compaiono termini con un fattore comune, possiamo raccogliere questo fattore per semplificare l'espressione.

Esempio di Fattorizzazione:

Consideriamo l'espressione: 15 + 20.

Entrambi i numeri sono divisibili per 5. Possiamo quindi riscrivere l'espressione come: 5 * 3 + 5 * 4.

Ora possiamo raccogliere il fattore comune 5: 5 * (3 + 4).

Calcoliamo la somma all'interno delle parentesi: 3 + 4 = 7.

Infine, moltiplichiamo: 5 * 7 = 35.

Errori Comuni e Come Evitarli

Anche i matematici più esperti possono commettere errori di calcolo. Tuttavia, essere consapevoli degli errori più comuni e adottare strategie per evitarli è fondamentale per garantire la correttezza dei risultati.

• Ignorare l'Ordine delle Operazioni: Questo è l'errore più frequente. Ricordate sempre l'acronimo PAMDAS e seguite l'ordine corretto.

• Errori di Segno: Prestate particolare attenzione ai segni positivi e negativi, soprattutto quando si lavora con sottrazioni e divisioni. Un piccolo errore di segno può alterare completamente il risultato.

• Errori di Trascrizione: Ricontrollate sempre i calcoli e verificate di aver trascritto correttamente i numeri e i simboli.

• Distrazione: La distrazione può portare a errori banali. Cercate di lavorare in un ambiente tranquillo e concentratevi sui calcoli.

Per evitare questi errori, è utile seguire le seguenti strategie:

• Scrivere Passo Passo: Non cercate di fare troppi calcoli a mente. Scrivete ogni passaggio in modo chiaro e ordinato.

• Ricontrollare i Calcoli: Dopo aver completato un calcolo, ricontrollatelo attentamente per individuare eventuali errori.

• Usare una Calcolatrice (con cautela): Una calcolatrice può essere uno strumento utile per velocizzare i calcoli, ma non affidatevi ciecamente ad essa. Verificate sempre che i risultati siano ragionevoli. Usare la calcolatrice solo per operazioni complesse, privilegiando il calcolo a mente per le operazioni più semplici.

• Chiedere Aiuto: Se siete bloccati o non siete sicuri di un calcolo, non abbiate paura di chiedere aiuto a un insegnante, a un compagno di classe o a un tutor.

Applicazioni Pratiche delle Espressioni Aritmetiche

Le espressioni aritmetiche non sono solo esercizi astratti. Trovano applicazioni concrete in una vasta gamma di contesti, dalla vita quotidiana alla scienza e alla tecnologia.

• Finanze Personali: Calcolare il budget mensile, determinare il tasso di interesse su un prestito o stimare il costo di un acquisto richiedono la capacità di manipolare espressioni aritmetiche.

• Cucina: Adattare una ricetta per un numero diverso di persone richiede la conoscenza delle proporzioni e la capacità di eseguire calcoli aritmetici.

• Costruzioni: Calcolare le dimensioni di un edificio, stimare la quantità di materiali necessari o determinare l'angolo di inclinazione di un tetto richiede l'uso di espressioni aritmetiche e geometriche.

• Programmazione: Le espressioni aritmetiche sono fondamentali nella programmazione informatica. Vengono utilizzate per eseguire calcoli, manipolare dati e controllare il flusso del programma.

• Scienza: In fisica, chimica, biologia e altre discipline scientifiche, le espressioni aritmetiche sono utilizzate per formulare leggi, analizzare dati e modellare fenomeni.

La padronanza delle espressioni aritmetiche è quindi una competenza essenziale per avere successo in molti ambiti della vita.

In conclusione, lo studio delle espressioni con le quattro operazioni è un viaggio attraverso il linguaggio fondamentale della matematica. Padroneggiare le regole di precedenza, applicare le proprietà delle operazioni e evitare gli errori comuni sono passi cruciali per navigare con sicurezza in questo regno. Ricordate, la precisione e la pratica costante sono i vostri migliori alleati in questo percorso. Continuate ad esplorare, a sperimentare e a mettere alla prova le vostre conoscenze. La matematica è un'avventura continua, ricca di scoperte e di soddisfazioni.