Espressioni Con Frazioni E Numeri Periodici

Ciao a tutti! Avete mai provato quel senso di panico quando vi trovate di fronte a un'espressione con frazioni e numeri periodici? Non siete soli! Molti studenti (e anche qualche adulto!) trovano queste espressioni un po' ostiche. Ma non temete! In questo articolo, vi guiderò passo passo attraverso le tecniche e i trucchi per domare queste espressioni, trasformando la frustrazione in successo matematico. L'articolo è pensato per studenti delle scuole medie e superiori, ma anche per chiunque voglia rinfrescare le proprie conoscenze matematiche.

Cosa sono le Frazioni e i Numeri Periodici?

Prima di addentrarci nelle espressioni, facciamo un breve ripasso dei concetti fondamentali:

Frazioni

Una frazione rappresenta una parte di un intero. È espressa nella forma a/b, dove a è il numeratore (il numero di parti che consideriamo) e b è il denominatore (il numero totale di parti in cui è diviso l'intero). Ricordatevi che il denominatore non può mai essere zero!

Numeri Periodici

Un numero periodico è un numero decimale in cui una cifra o un gruppo di cifre (il periodo) si ripete all'infinito. Ad esempio, 1/3 = 0,3333... è un numero periodico semplice, mentre 1/7 = 0,142857142857... è un numero periodico composto.

Periodo semplice: il periodo inizia subito dopo la virgola (es. 0,6666...).
Periodo misto: c'è una parte non periodica tra la virgola e il periodo (es. 0,16666...).

Trasformare i Numeri Periodici in Frazioni

Il passaggio fondamentale per risolvere espressioni con numeri periodici è trasformarli in frazioni. Ecco le regole:

Periodo Semplice

Per trasformare un numero periodico semplice in frazione, scrivete il periodo al numeratore e al denominatore un numero composto da tanti 9 quante sono le cifre del periodo. Ad esempio:

0,3333... = 3/9 = 1/3
0,7777... = 7/9
0,232323... = 23/99

Periodo Misto

Per trasformare un numero periodico misto in frazione, sottraete al numero intero, senza la virgola, la parte non periodica, e scrivete il risultato al numeratore. Al denominatore, scrivete un numero composto da tanti 9 quante sono le cifre del periodo e tanti 0 quante sono le cifre dell'antiperiodo (la parte non periodica tra la virgola e il periodo). Ad esempio:

0,16666... = (16 - 1) / 90 = 15/90 = 1/6
2,345555... = (2345 - 234) / 900 = 2111/900

Esempio pratico: Trasformiamo 1,2(3) in frazione (dove (3) indica che il 3 è periodico):

Numero intero senza virgola: 123
Parte non periodica: 12
Numeratore: 123 - 12 = 111
Denominatore: un 9 (per il periodo) e uno 0 (per l'antiperiodo) = 90
Frazione: 111/90 = 37/30

Risolvere le Espressioni: L'Ordine delle Operazioni

Una volta che abbiamo trasformato tutti i numeri periodici in frazioni, possiamo affrontare l'espressione. È fondamentale seguire l'ordine delle operazioni:

Parentesi: Risolvere prima le operazioni all'interno delle parentesi (tonde, quadre, graffe).
Potenze e radici: Calcolare potenze e radici.
Moltiplicazioni e divisioni: Eseguire moltiplicazioni e divisioni nell'ordine in cui compaiono.
Addizioni e sottrazioni: Eseguire addizioni e sottrazioni nell'ordine in cui compaiono.

Operazioni con le Frazioni

Ricordiamoci le regole per le operazioni con le frazioni:

Addizione e Sottrazione

Per sommare o sottrarre frazioni, devono avere lo stesso denominatore. Se non lo hanno, dobbiamo trovare il minimo comune multiplo (MCM) dei denominatori e ridurre le frazioni al minimo comune denominatore.

Esempio: 1/2 + 1/3 = (3/6) + (2/6) = 5/6

Moltiplicazione

Per moltiplicare due frazioni, moltiplicate i numeratori tra loro e i denominatori tra loro.

Esempio: (1/2) * (2/3) = (1*2) / (2*3) = 2/6 = 1/3

Divisione

Per dividere due frazioni, moltiplicate la prima frazione per l'inverso della seconda frazione.

Esempio: (1/2) / (2/3) = (1/2) * (3/2) = 3/4

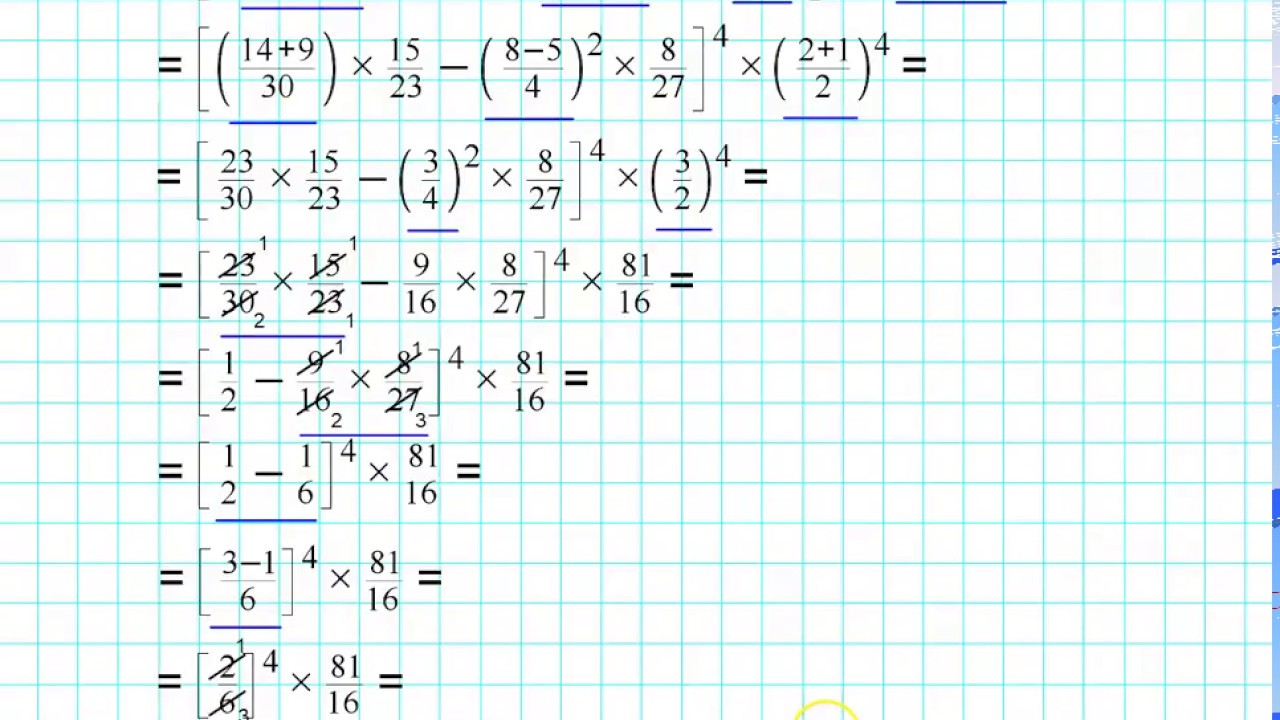
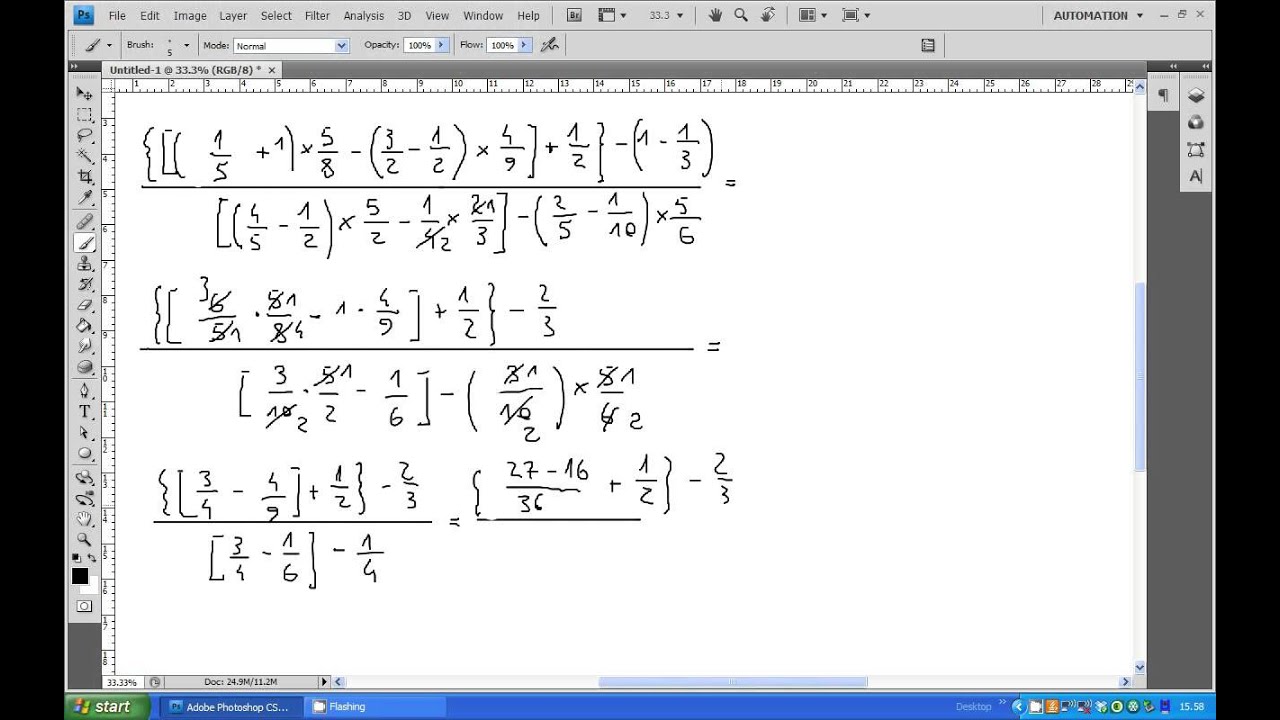
Esempi Pratici Risolti

Vediamo alcuni esempi di espressioni con frazioni e numeri periodici, risolti passo passo:

Esempio 1

(0,3333... + 1/4) * 2

Trasformiamo 0,3333... in frazione: 0,3333... = 1/3
Sostituiamo: (1/3 + 1/4) * 2
Troviamo il MCM di 3 e 4: MCM(3, 4) = 12
Riduciamo le frazioni al minimo comune denominatore: (4/12 + 3/12) * 2
Sommiamo le frazioni: (7/12) * 2
Moltiplichiamo: 7/12 * 2 = 14/12 = 7/6

Esempio 2

(1,6666... - 1/2) / (2/3)

Trasformiamo 1,6666... in frazione: 1,6666... = (16 - 1)/9 = 15/9 = 5/3
Sostituiamo: (5/3 - 1/2) / (2/3)
Troviamo il MCM di 3 e 2: MCM(3, 2) = 6
Riduciamo le frazioni al minimo comune denominatore: (10/6 - 3/6) / (2/3)
Sottraiamo le frazioni: (7/6) / (2/3)
Dividiamo: (7/6) * (3/2) = 21/12 = 7/4

Esempio 3

[1/2 + 0,2(3)] * (3/4 - 1/8)

Trasformiamo 0,2(3) in frazione: 0,2(3) = (23-2)/90 = 21/90 = 7/30
Sostituiamo: [1/2 + 7/30] * (3/4 - 1/8)
Calcoliamo la prima parentesi quadra: MCM(2, 30) = 30. Quindi [15/30 + 7/30] = 22/30 = 11/15
Calcoliamo la seconda parentesi tonda: MCM(4, 8) = 8. Quindi (6/8 - 1/8) = 5/8
Moltiplichiamo: (11/15) * (5/8) = 55/120 = 11/24

Trucchi e Consigli Utili

Semplificare le frazioni: Prima di iniziare qualsiasi operazione, semplificate le frazioni al massimo. Questo vi renderà la vita più facile.
Essere ordinati: Scrivete tutti i passaggi in modo chiaro e ordinato. Questo vi aiuterà a evitare errori.
Controllare i risultati: Una volta ottenuto il risultato, controllatelo. Potete usare una calcolatrice online per verificare se avete fatto tutto correttamente.
Fare pratica: La pratica rende perfetti! Più espressioni risolvete, più diventerete bravi.
Non aver paura di chiedere aiuto: Se vi bloccate, non esitate a chiedere aiuto al vostro insegnante, a un compagno di classe o a un tutor.
Ricorda le proprietà delle operazioni: Associativa, commutativa, distributiva, etc.
Attenzione ai segni: Un errore di segno può compromettere l'intero risultato.

Applicazioni Pratiche

Le espressioni con frazioni e numeri periodici non sono solo un esercizio scolastico. Hanno applicazioni pratiche in molti campi, come:

Cucina: Ad esempio, quando dovete dimezzare o raddoppiare una ricetta.
Finanza: Calcolo di interessi e commissioni.
Ingegneria: Calcolo di proporzioni e scale.
Programmazione: Conversione di unità di misura.

Conclusione

Spero che questo articolo vi abbia fornito gli strumenti e le conoscenze necessarie per affrontare con confidenza le espressioni con frazioni e numeri periodici. Ricordatevi che la chiave è la pratica e la comprensione dei concetti fondamentali. Non abbiate paura di fare errori, perché è proprio dagli errori che si impara. Con un po' di impegno e determinazione, diventerete dei veri e propri maestri delle espressioni! In bocca al lupo!