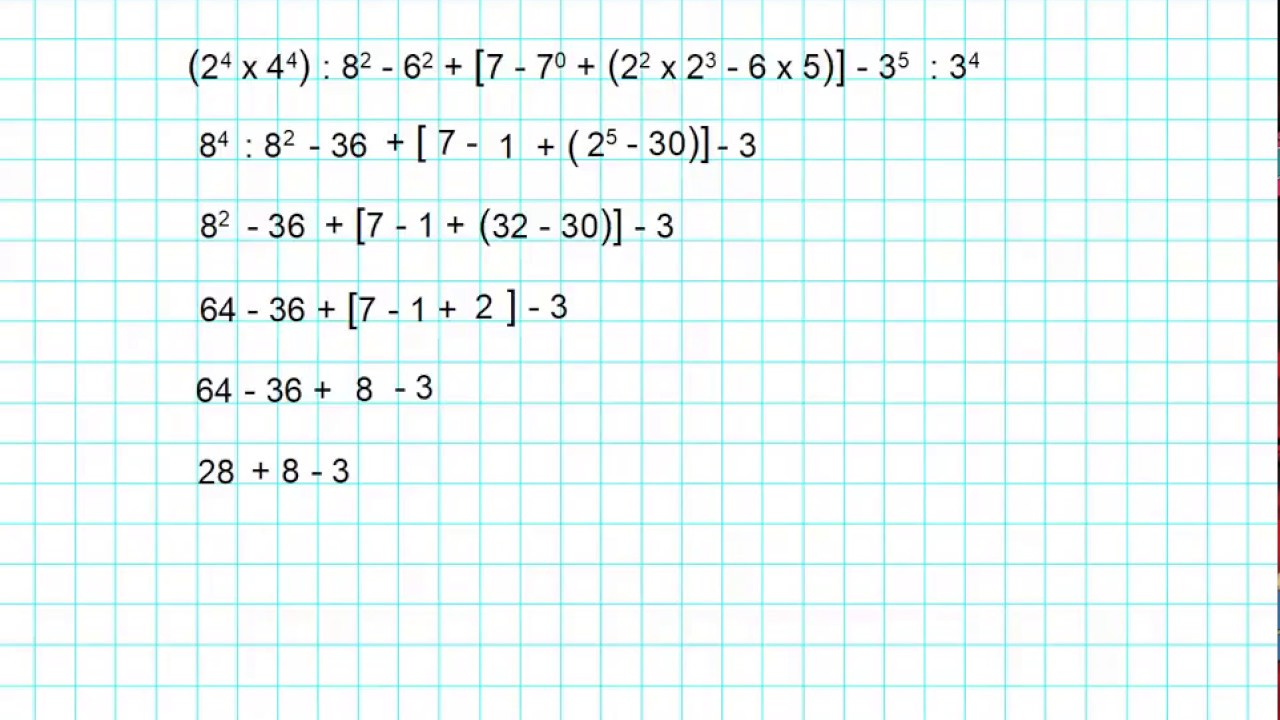Espressione Con Le Proprietà Delle Potenze

Capita a tutti, prima o poi, di trovarsi di fronte a un'espressione matematica piena zeppa di potenze. Numeri piccoli in alto a destra che, a prima vista, sembrano complicare inutilmente la vita. Ma non temere! Dietro a questi piccoli simboli si celano regole precise e potenti, capaci di semplificare calcoli altrimenti lunghissimi e noiosi. Questo articolo è pensato per te, che magari ti senti un po' spaesato di fronte alle proprietà delle potenze. Cercheremo di rendere tutto più chiaro, partendo dalle basi e arrivando a esempi pratici.

Cosa Sono le Potenze e Perché Sono Utili?

Innanzitutto, cerchiamo di capire cos'è una potenza. In parole semplici, una potenza è un modo abbreviato per scrivere una moltiplicazione ripetuta dello stesso numero. Ad esempio, invece di scrivere 2 * 2 * 2 * 2 * 2, possiamo scrivere 2⁵. Il numero 2 è la base, mentre il numero 5 è l'esponente. L'esponente indica quante volte la base deve essere moltiplicata per se stessa.

Perché usare le potenze? Immagina di dover calcolare l'area di un quadrato con lato di 1000 metri. Dovresti fare 1000 * 1000, che è uguale a 1.000.000. Scritto in forma di potenza, sarebbe 10⁶. Molto più compatto, no? Le potenze diventano indispensabili quando si ha a che fare con numeri molto grandi o molto piccoli, come quelli che si incontrano in fisica, chimica o astronomia.

Potenze con Esponente Positivo Intero

Cominciamo con le potenze più semplici, quelle con esponente positivo intero. Come abbiamo visto, aⁿ significa moltiplicare la base a per se stessa n volte.

Esempio: 3⁴ = 3 * 3 * 3 * 3 = 81

Potenze con Esponente Zero

Cosa succede se l'esponente è zero? Per convenzione, qualsiasi numero (diverso da zero) elevato a zero è uguale a 1. Questa regola può sembrare strana all'inizio, ma deriva dalle proprietà che vedremo a breve. In sostanza, a⁰ = 1 (con a ≠ 0).

Esempio: 5⁰ = 1
Esempio: (-2)⁰ = 1

Un punto importante: 0⁰ è una forma indeterminata, e il suo valore non è definito.

Potenze con Esponente Negativo Intero

Se l'esponente è negativo, significa che dobbiamo calcolare l'inverso della potenza con esponente positivo. In altre parole, a^-n = 1 / aⁿ.

Esempio: 2^-3 = 1 / 2³ = 1 / 8
Esempio: 5^-1 = 1 / 5

Potenze con Esponente Frazionario

Quando l'esponente è una frazione, stiamo parlando di radici. In generale, a^m/n = ⁿ√a^m. Quindi, una potenza con esponente frazionario rappresenta la radice n-esima di a elevato a m.

Esempio: 4^1/2 = √4 = 2 (radice quadrata di 4)
Esempio: 8^2/3 = ³√8² = ³√64 = 4 (radice cubica di 8 al quadrato)

Le Proprietà Fondamentali delle Potenze

Ora veniamo al cuore del discorso: le proprietà delle potenze. Queste regole ci permettono di semplificare espressioni complesse e risolvere problemi in modo più efficiente.

1. Prodotto di Potenze con la Stessa Base

Quando moltiplichiamo due potenze con la stessa base, possiamo sommare gli esponenti: a^m * aⁿ = a^m+n.

Esempio: 2³ * 2² = 2³⁺² = 2⁵ = 32

2. Quoziente di Potenze con la Stessa Base

Quando dividiamo due potenze con la stessa base, possiamo sottrarre gli esponenti: a^m / aⁿ = a^m-n.

Esempio: 5⁴ / 5² = 5^4-2 = 5² = 25

3. Potenza di una Potenza

Quando eleviamo una potenza a un altro esponente, possiamo moltiplicare gli esponenti: (a^m)ⁿ = a^m*n.

Esempio: (3²)³ = 3^2*3 = 3⁶ = 729

4. Prodotto di Potenze con lo Stesso Esponente

Quando moltiplichiamo due potenze con lo stesso esponente, possiamo moltiplicare le basi e mantenere l'esponente: aⁿ * bⁿ = (a*b)ⁿ.

Esempio: 2³ * 5³ = (2*5)³ = 10³ = 1000

5. Quoziente di Potenze con lo Stesso Esponente

Quando dividiamo due potenze con lo stesso esponente, possiamo dividere le basi e mantenere l'esponente: aⁿ / bⁿ = (a/b)ⁿ.

Esempio: 6² / 3² = (6/3)² = 2² = 4

Errori Comuni e Come Evitarli

È facile commettere errori quando si lavora con le potenze, soprattutto all'inizio. Ecco alcuni errori comuni da evitare:

Confondere la somma di potenze con il prodotto di potenze: a^m + aⁿ non è uguale a a^m+n! La proprietà vale solo per la moltiplicazione.
Dimenticare l'importanza dei segni: Ricorda che un numero negativo elevato a un esponente pari dà un risultato positivo, mentre elevato a un esponente dispari dà un risultato negativo.
Non semplificare prima di calcolare: Prima di iniziare a fare calcoli complessi, cerca sempre di semplificare l'espressione usando le proprietà delle potenze. Questo ti farà risparmiare tempo e fatica.

Applicazioni Pratiche delle Proprietà delle Potenze

Le proprietà delle potenze non sono solo esercizi di matematica astratta. Hanno applicazioni concrete in molti campi:

Informatica: Le potenze di 2 sono fondamentali nell'informatica, perché i computer utilizzano il sistema binario (base 2). La memoria di un computer è misurata in byte, che sono potenze di 2.
Scienza: In fisica e chimica, le potenze di 10 sono usate per esprimere grandezze molto grandi o molto piccole, come la velocità della luce o la massa di un atomo.
Finanza: Il calcolo degli interessi composti si basa sulle potenze.
Ingegneria: Le potenze sono utilizzate per calcolare l'area, il volume e altre grandezze geometriche.

Consideriamo un esempio concreto: il calcolo dell'area di un cerchio. La formula è Area = πr², dove π (pi greco) è una costante e r è il raggio del cerchio. Se il raggio è 5 cm, l'area sarà π * 5² = π * 25 ≈ 78.54 cm². La potenza 2 ci permette di calcolare l'area in modo semplice e veloce.

Controindicazioni e Approcci Alternativi

Alcuni potrebbero sostenere che imparare le proprietà delle potenze è obsoleto nell'era delle calcolatrici e dei computer. È vero che questi strumenti possono eseguire calcoli complessi in pochi secondi. Tuttavia, comprendere i principi matematici sottostanti è fondamentale per sviluppare un pensiero critico e risolvere problemi in modo efficace. Conoscere le proprietà delle potenze ti permette di capire come funzionano gli algoritmi che utilizzano le calcolatrici e i computer, e di interpretare correttamente i risultati.

Inoltre, in alcune situazioni, avere una buona padronanza delle proprietà delle potenze può permetterti di fare calcoli a mente o su carta, senza bisogno di strumenti esterni. Questo può essere utile in situazioni di emergenza o quando non hai accesso a una calcolatrice.

Un Esempio Complesso: Semplificazione di un'Espressione

Prendiamo un esempio più complesso per mettere in pratica le proprietà delle potenze:

(8² * 4^-1) / 2³

Possiamo riscrivere tutto in termini di potenze di 2:

((2³)² * (2²)^-1) / 2³

Applicando la proprietà della potenza di una potenza:

(2⁶ * 2^-2) / 2³

Applicando la proprietà del prodotto di potenze con la stessa base:

2⁴ / 2³

Applicando la proprietà del quoziente di potenze con la stessa base:

2¹ = 2

Come vedi, semplificando l'espressione usando le proprietà delle potenze, siamo arrivati a un risultato molto semplice.

Un Passo Alla Volta: Consigli per l'Apprendimento

Ecco alcuni consigli per imparare le proprietà delle potenze in modo efficace:

Parti dalle basi: Assicurati di aver capito bene le definizioni e le proprietà fondamentali prima di affrontare problemi più complessi.
Fai tanti esercizi: La pratica è fondamentale per memorizzare le proprietà e imparare a applicarle correttamente.
Cerca esempi pratici: Cerca di capire come le potenze vengono utilizzate in contesti reali.
Non aver paura di chiedere aiuto: Se hai difficoltà, chiedi aiuto al tuo insegnante, ai tuoi compagni di classe o cerca risorse online.
Utilizza risorse online: Esistono molti siti web e video tutorial che possono aiutarti a capire le proprietà delle potenze.

Ricorda, l'apprendimento è un processo graduale. Non scoraggiarti se all'inizio ti sembra difficile. Con la pratica e la perseveranza, diventerai sempre più bravo a usare le proprietà delle potenze.

Le proprietà delle potenze, sebbene a volte appaiano come un insieme di regole astratte, sono uno strumento potentissimo per semplificare calcoli e risolvere problemi in diversi ambiti. Averle comprese e sapute applicare correttamente, ti aprirà le porte a una comprensione più profonda della matematica e delle sue applicazioni nel mondo reale.

Quindi, sei pronto a mettere in pratica le tue nuove conoscenze e affrontare la prossima espressione con le potenze con più sicurezza e competenza?