Esercizi Sui Vettori Fisica Prima Liceo Con Soluzioni

Ciao ragazzi di prima liceo! So che state affrontando un argomento nuovo e a volte un po' ostico: i vettori. Non preoccupatevi, è assolutamente normale sentirsi un po' spaesati all'inizio. La fisica può sembrare astratta, ma vi assicuro che è ovunque intorno a noi. Pensate a quando tirate un pallone, a quando spingete un carrello della spesa, o semplicemente a quando camminate: in tutti questi casi, i vettori sono protagonisti!

Questo articolo è pensato proprio per voi, per aiutarvi a capire meglio i vettori e a risolvere gli esercizi più comuni. Cercheremo di semplificare i concetti e di affrontare i problemi passo dopo passo, fornendovi anche le soluzioni per controllare i vostri risultati. L'obiettivo è rendere questo argomento accessibile e, perché no, anche un po' divertente!

Perché Studiare i Vettori? L'Importanza Nella Vita Reale

Prima di tuffarci negli esercizi, cerchiamo di capire perché i vettori sono così importanti. Non sono solo un argomento di fisica che dovete studiare per il compito in classe. I vettori sono fondamentali per descrivere e comprendere il mondo che ci circonda.

Pensate alla navigazione aerea: i piloti utilizzano i vettori per calcolare la rotta, tenendo conto della velocità del vento e della direzione dell'aereo. Oppure, immaginate un ingegnere che deve progettare un ponte: deve considerare le forze che agiscono sulla struttura, e queste forze sono rappresentate proprio da vettori.

Anche nello sport i vettori giocano un ruolo importante. Ad esempio, un giocatore di calcio deve calcolare la forza e la direzione con cui colpire la palla per fare goal. Un arciere deve tenere conto della forza del vento e dell'angolo di tiro per centrare il bersaglio.

Quindi, studiare i vettori non significa solo imparare delle formule, ma acquisire uno strumento potente per analizzare e interpretare la realtà che ci circonda. Vi aiuterà a sviluppare il vostro pensiero critico e la vostra capacità di risolvere problemi.

Concetti Fondamentali Sui Vettori

Prima di affrontare gli esercizi, ripassiamo brevemente i concetti fondamentali sui vettori:

• Definizione: Un vettore è un ente matematico caratterizzato da modulo (o intensità), direzione e verso. Possiamo immaginarlo come una freccia.
• Modulo: Rappresenta la lunghezza del vettore, ovvero la sua "intensità". È un numero sempre positivo.
• Direzione: È la retta su cui giace il vettore.
• Verso: Indica l'orientamento del vettore lungo la sua direzione (ad esempio, verso destra o verso sinistra).
• Rappresentazione: I vettori si rappresentano graficamente con una freccia e si indicano con una lettera sormontata da una freccia (es. ⃑v) oppure in grassetto (es. v).
• Operazioni con i vettori: Possiamo sommare, sottrarre e moltiplicare i vettori (con alcune limitazioni).

È importante avere ben chiari questi concetti prima di affrontare gli esercizi. Se avete dubbi, ripassateli sul vostro libro di testo o chiedete al vostro insegnante.

Esercizi Sui Vettori: Pronti a Mettervi Alla Prova?

Ora che abbiamo ripassato la teoria, è il momento di passare alla pratica. Ecco alcuni esercizi tipici che potreste trovare nei compiti in classe o nelle verifiche. Cercheremo di risolverli insieme, passo dopo passo, spiegando il ragionamento e fornendo la soluzione corretta.

Esercizio 1: Somma di Vettori (Metodo Grafico)

Testo: Dati due vettori a e b rappresentati graficamente, con modulo |a| = 5 cm e |b| = 3 cm, formanti un angolo di 60° tra loro, determinare il vettore somma r = a + b utilizzando il metodo del parallelogramma.

Soluzione:

1. Disegnare i vettori: Disegnate i vettori a e b rispettando i moduli (usando una scala opportuna, ad esempio 1 cm = 1 unità) e l'angolo di 60° tra loro.
2. Costruire il parallelogramma: Costruite un parallelogramma avente i vettori a e b come lati adiacenti.
3. Tracciare la diagonale: Tracciate la diagonale del parallelogramma che parte dal punto di applicazione comune dei vettori a e b. Questa diagonale rappresenta il vettore somma r.
4. Misurare il modulo: Misurate la lunghezza della diagonale (il modulo del vettore r) con un righello e applicate la scala per ottenere il valore reale. Il modulo di r sarà circa 7.2 cm.
5. Misurare l'angolo: Misurate l'angolo che il vettore r forma con uno dei vettori originali (ad esempio, con il vettore a) utilizzando un goniometro. Questo angolo vi fornirà la direzione del vettore r rispetto al vettore a.

Risposta: Il vettore somma r ha un modulo di circa 7.2 cm e forma un angolo di circa 34° con il vettore a.

Esercizio 2: Somma di Vettori (Metodo Analitico)

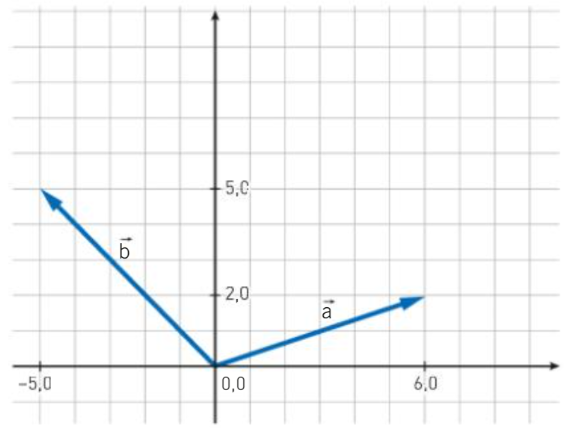
Testo: Dati due vettori a = (3, 4) e b = (-1, 2), calcolare il vettore somma r = a + b.

Soluzione:

1. Sommare le componenti: Per sommare i vettori in forma analitica, è sufficiente sommare le componenti corrispondenti:
   • r_x = a_x + b_x = 3 + (-1) = 2
   • r_y = a_y + b_y = 4 + 2 = 6
2. Scrivere il vettore somma: Il vettore somma r sarà quindi r = (2, 6).

Risposta: Il vettore somma r è r = (2, 6).

Esercizio 3: Differenza di Vettori

Testo: Dati due vettori a = (5, 2) e b = (1, -3), calcolare il vettore differenza d = a - b.

Soluzione:

1. Sottrarre le componenti: Per sottrarre i vettori in forma analitica, è sufficiente sottrarre le componenti corrispondenti:
   • d_x = a_x - b_x = 5 - 1 = 4
   • d_y = a_y - b_y = 2 - (-3) = 5
2. Scrivere il vettore differenza: Il vettore differenza d sarà quindi d = (4, 5).

Risposta: Il vettore differenza d è d = (4, 5).

Esercizio 4: Calcolo del Modulo di un Vettore

Testo: Calcolare il modulo del vettore v = (3, -4).

Soluzione:

1. Applicare il teorema di Pitagora: Il modulo di un vettore in due dimensioni si calcola utilizzando il teorema di Pitagora: |v| = √(v_x² + v_y²)
2. Sostituire i valori: Sostituiamo i valori delle componenti del vettore: |v| = √(3² + (-4)²) = √(9 + 16) = √25 = 5

Risposta: Il modulo del vettore v è |v| = 5.

Esercizio 5: Scomposizione di un Vettore

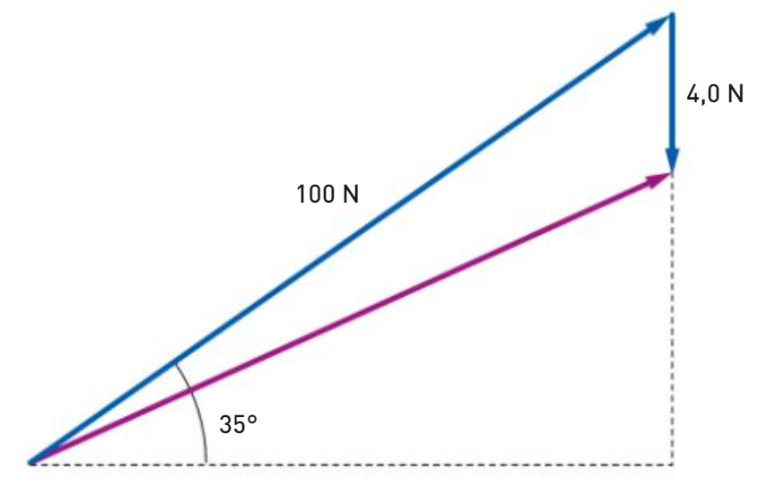
Testo: Un vettore forza F ha un modulo di 10 N e forma un angolo di 30° con l'asse x. Calcolare le componenti F_x e F_y del vettore.

Soluzione:

1. Utilizzare le funzioni trigonometriche: Le componenti del vettore si calcolano utilizzando le funzioni trigonometriche seno e coseno:
   • F_x = |F| * cos(θ)
   • F_y = |F| * sin(θ)
2. Sostituire i valori: Sostituiamo i valori del modulo e dell'angolo:
   • F_x = 10 N * cos(30°) = 10 N * (√3 / 2) ≈ 8.66 N
   • F_y = 10 N * sin(30°) = 10 N * (1 / 2) = 5 N

Risposta: Le componenti del vettore forza F sono F_x ≈ 8.66 N e F_y = 5 N.

Consigli Utili per Risolvere gli Esercizi Sui Vettori

Ecco alcuni consigli che vi saranno utili per affrontare gli esercizi sui vettori con maggiore sicurezza:

• Fate un disegno: Rappresentare graficamente i vettori vi aiuterà a visualizzare il problema e a capire meglio le relazioni tra le diverse grandezze.
• Scegliete il metodo giusto: A seconda del tipo di problema, può essere più conveniente utilizzare il metodo grafico o il metodo analitico. Imparate a riconoscere quale metodo è più adatto per ogni situazione.
• Rivedete le formule: Assicuratevi di conoscere bene le formule per sommare, sottrarre, calcolare il modulo e scomporre i vettori.
• Verificate le unità di misura: Controllate sempre che le unità di misura siano coerenti tra loro.
• Esercitatevi: Più vi esercitate, più diventerete bravi a risolvere i problemi sui vettori. Non abbiate paura di sbagliare, perché è sbagliando che si impara!

Cosa Fare se Incontrate Difficoltà?

È normale incontrare difficoltà quando si studia un argomento nuovo. Se vi sentite bloccati, non scoraggiatevi! Ecco alcune cose che potete fare:

• Rileggete il vostro libro di testo: A volte, rileggere la teoria con calma può aiutarvi a chiarire i dubbi.
• Chiedete aiuto al vostro insegnante: Il vostro insegnante è lì per aiutarvi! Non esitate a porgli le vostre domande.
• Studiate con i vostri compagni: Studiare in gruppo può essere un modo efficace per confrontarsi e superare le difficoltà insieme.
• Cercate risorse online: Ci sono molti siti web e video tutorial che possono aiutarvi a capire meglio i vettori.

Conclusioni

Spero che questo articolo vi sia stato utile per capire meglio i vettori e per affrontare gli esercizi con maggiore sicurezza. Ricordate, la fisica non è solo un insieme di formule, ma un modo per comprendere il mondo che ci circonda. Con un po' di impegno e di curiosità, potrete scoprire la bellezza e l'utilità di questa materia.

Ora, provate a risolvere da soli gli esercizi che abbiamo visto insieme e cercate altri problemi online o sul vostro libro di testo. Quali altri argomenti di fisica vi mettono in difficoltà e vorreste che affrontassimo insieme in futuro?