Equazioni Differenziali Primo Ordine Esercizi Svolti

Ciao! Se sei qui, probabilmente stai lottando con le equazioni differenziali del primo ordine. Non preoccuparti, capita a tutti! Sono un argomento fondamentale in matematica e fisica, ma possono sembrare ostici all'inizio. Molti studenti si bloccano di fronte alla vastità di metodi e tecniche diverse, e non è facile capire quale applicare in ogni situazione. La difficoltà sta spesso nel tradurre un problema del mondo reale in un'equazione matematica risolvibile, e viceversa, interpretare la soluzione ottenuta nel contesto originale. Questo articolo è pensato proprio per aiutarti a superare queste difficoltà, offrendoti una guida pratica con esercizi svolti passo dopo passo. Cercheremo di affrontare i problemi più comuni e di fornirti gli strumenti necessari per affrontare con sicurezza questo argomento.

Le equazioni differenziali del primo ordine descrivono una vasta gamma di fenomeni, dalla crescita di una popolazione alla velocità di raffreddamento di un oggetto. Pensaci: la velocità con cui si diffonde un'epidemia, la scarica di un condensatore in un circuito elettrico, la traiettoria di un proiettile... tutti questi processi possono essere modellati usando equazioni differenziali. Capire come risolverle significa avere un potente strumento per analizzare e prevedere il comportamento di sistemi complessi. Al contrario, non saperle risolvere ti lascerebbe all'oscuro del "dietro le quinte" di molti processi naturali e tecnologici che influenzano la nostra vita quotidiana.

Equazioni Differenziali del Primo Ordine: Un Ripasso Teorico

Prima di tuffarci negli esercizi, facciamo un breve ripasso dei concetti fondamentali. Un'equazione differenziale del primo ordine è un'equazione che coinvolge una funzione incognita y(x) e la sua derivata prima y'(x). In forma generale, possiamo scriverla come:

F(x, y, y') = 0

Dove F è una funzione di tre variabili. Risolvere un'equazione differenziale significa trovare tutte le funzioni y(x) che soddisfano l'equazione. Queste soluzioni possono essere esplicite (y = f(x)) o implicite (G(x, y) = C, dove C è una costante).

Esistono diversi tipi di equazioni differenziali del primo ordine, ciascuna con le sue tecniche di risoluzione. Le più comuni sono:

• Equazioni a variabili separabili: Possono essere scritte nella forma g(y)y' = h(x). Si risolvono integrando entrambi i membri rispetto a x.
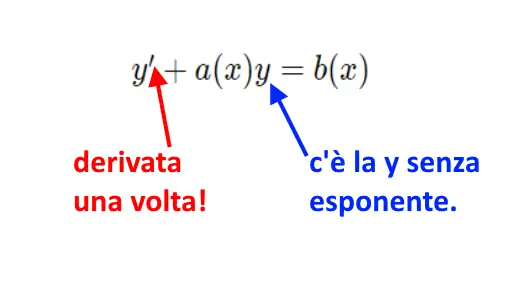
• Equazioni lineari: Possono essere scritte nella forma y' + p(x)y = q(x). Si risolvono usando il fattore integrante.
• Equazioni esatte: Possono essere scritte nella forma M(x, y) + N(x, y)y' = 0, dove ∂M/∂y = ∂N/∂x. Si risolvono trovando una funzione Φ(x, y) tale che ∂Φ/∂x = M e ∂Φ/∂y = N.
• Equazioni omogenee: Possono essere scritte nella forma y' = f(y/x). Si risolvono effettuando la sostituzione v = y/x.

Esercizi Svolti Passo dopo Passo

Ora passiamo alla parte più interessante: gli esercizi! Analizzeremo alcuni esempi tipici, spiegando il procedimento risolutivo in dettaglio.

Esercizio 1: Equazione a Variabili Separabili

Risolvere l'equazione differenziale:

y' = x / y

Soluzione:

1. Separiamo le variabili: Moltiplichiamo entrambi i membri per y e per dx (ricordando che y' = dy/dx):

y dy = x dx

2. Integriamo entrambi i membri:

∫ y dy = ∫ x dx

(1/2)y² = (1/2)x² + C

3. Risolviamo per y: Moltiplichiamo per 2 e prendiamo la radice quadrata:

y² = x² + 2C

y = ±√(x² + K) (dove K = 2C è una nuova costante arbitraria)

Quindi, la soluzione generale è y = ±√(x² + K).

Esercizio 2: Equazione Lineare del Primo Ordine

Risolvere l'equazione differenziale:

y' + 2y = e^-x

Soluzione:

1. Identifichiamo p(x) e q(x): In questo caso, p(x) = 2 e q(x) = e^-x.
2. Calcoliamo il fattore integrante: Il fattore integrante è dato da μ(x) = e^∫p(x)dx. Quindi:

μ(x) = e^∫2dx = e^2x

3. Moltiplichiamo l'equazione per il fattore integrante:

e^2xy' + 2e^2xy = e^x

4. Riconosciamo la derivata del prodotto: Il membro sinistro è la derivata di e^2xy:

(e^2xy)' = e^x

5. Integriamo entrambi i membri:

∫(e^2xy)' dx = ∫e^x dx

e^2xy = e^x + C

6. Risolviamo per y:

y = e^-x + Ce^-2x

Quindi, la soluzione generale è y = e^-x + Ce^-2x.

Esercizio 3: Equazione Esatta

Risolvere l'equazione differenziale:

(2x + y) + (x + 3y²)y' = 0

Soluzione:

1. Identifichiamo M(x, y) e N(x, y): In questo caso, M(x, y) = 2x + y e N(x, y) = x + 3y².
2. Verifichiamo se l'equazione è esatta: Calcoliamo le derivate parziali:

∂M/∂y = 1

∂N/∂x = 1

Poiché ∂M/∂y = ∂N/∂x, l'equazione è esatta.

3. Troviamo la funzione Φ(x, y): Dobbiamo trovare una funzione tale che ∂Φ/∂x = M e ∂Φ/∂y = N. Integriamo M rispetto a x:

Φ(x, y) = ∫M dx = ∫(2x + y) dx = x² + xy + g(y)

Dove g(y) è una funzione arbitraria di y. Ora deriviamo Φ rispetto a y:

∂Φ/∂y = x + g'(y)

E uguagliamo a N(x, y):

x + g'(y) = x + 3y²

Quindi, g'(y) = 3y². Integriamo per trovare g(y):

g(y) = ∫3y² dy = y³

Quindi, Φ(x, y) = x² + xy + y³.

4. La soluzione è data da Φ(x, y) = C:

x² + xy + y³ = C

Quindi, la soluzione generale è x² + xy + y³ = C.

Esercizio 4: Equazione Omogenea

Risolvere l'equazione differenziale:

y' = (x² + y²) / (xy)

Soluzione:

1. Verifichiamo se l'equazione è omogenea: Possiamo riscrivere l'equazione come:

y' = (x/y) + (y/x)

Quindi, è una funzione di y/x, ed è omogenea.

2. Effettuiamo la sostituzione v = y/x: Quindi, y = vx e y' = v + xv'. Sostituiamo nell'equazione originale:

v + xv' = (1/v) + v

3. Semplifichiamo:

xv' = 1/v

4. Separiamo le variabili:

v dv = (1/x) dx

5. Integriamo entrambi i membri:

∫v dv = ∫(1/x) dx

(1/2)v² = ln|x| + C

6. Sostituiamo v = y/x:

(1/2)(y/x)² = ln|x| + C

7. Risolviamo per y (opzionale):

y² = 2x²(ln|x| + C)

y = ±x√(2ln|x| + K) (dove K = 2C)

Quindi, la soluzione generale è y = ±x√(2ln|x| + K) oppure, in forma implicita, (1/2)(y/x)² = ln|x| + C.

Consigli Utili per la Risoluzione

Risolvere equazioni differenziali richiede pratica e una buona comprensione dei concetti fondamentali. Ecco alcuni consigli che potrebbero esserti utili:

• Identifica il tipo di equazione: Prima di iniziare a risolvere, cerca di capire a quale categoria appartiene l'equazione. Questo ti guiderà nella scelta del metodo appropriato.
• Ricorda le regole di integrazione: L'integrazione è una parte fondamentale del processo di risoluzione. Assicurati di avere una buona padronanza delle tecniche di integrazione.
• Sii preciso nei calcoli: Un piccolo errore di calcolo può portare a una soluzione errata. Controlla attentamente ogni passaggio.
• Verifica la soluzione: Una volta trovata una soluzione, sostituiscila nell'equazione originale per verificare se è corretta.
• Pratica, pratica, pratica: Più esercizi svolgi, più diventerai bravo a risolvere equazioni differenziali.
• Non aver paura di chiedere aiuto: Se ti blocchi, non esitare a chiedere aiuto al tuo professore, ai tuoi compagni di corso o a risorse online.

Oltre la Teoria: Applicazioni Pratiche

Le equazioni differenziali del primo ordine non sono solo un esercizio accademico. Hanno applicazioni concrete in molti campi:

• Fisica: Modellano il movimento di oggetti, la crescita di onde, la decadenza radioattiva e molti altri fenomeni. Ad esempio, la legge di Newton del raffreddamento è un'equazione differenziale del primo ordine.
• Ingegneria: Sono utilizzate per progettare circuiti elettrici, sistemi di controllo e strutture meccaniche. La modellazione della risposta di un sistema a un ingresso è spesso basata su equazioni differenziali.
• Biologia: Descrivono la crescita di popolazioni, la diffusione di malattie e la dinamica di reazioni chimiche. Il modello di crescita logistica è un esempio classico.
• Economia: Modellano l'andamento dei mercati finanziari, la crescita economica e la dinamica dei prezzi.

Questi sono solo alcuni esempi. Le equazioni differenziali sono uno strumento fondamentale per comprendere e modellare il mondo che ci circonda. Comprendere le equazioni differenziali non significa solo saperle risolvere, ma anche saperle applicare per risolvere problemi concreti.

Affrontare le Difficoltà Comuni

Molti studenti incontrano difficoltà simili quando studiano le equazioni differenziali del primo ordine. Ecco alcuni dei problemi più comuni e come affrontarli:

• Difficoltà a identificare il tipo di equazione: Esercitati a riconoscere le diverse forme di equazioni differenziali. Crea una "checklist" mentale per ogni tipo di equazione.
• Errori nell'integrazione: Rivedi le regole di integrazione e fai pratica con integrali difficili. Usa tabelle di integrali o software di calcolo per controllare i tuoi risultati.
• Confusione con le condizioni iniziali: Ricorda che le condizioni iniziali servono a determinare il valore delle costanti arbitrarie nella soluzione generale.
• Difficoltà a interpretare la soluzione: Cerca di capire cosa significa la soluzione nel contesto del problema. Disegna il grafico della soluzione e analizza il suo comportamento.

Ricorda che la perseveranza è fondamentale. Non scoraggiarti se incontri difficoltà. Continua a studiare, a fare esercizi e a chiedere aiuto quando necessario. Con il tempo, le equazioni differenziali del primo ordine diventeranno sempre più facili da affrontare.

Abbiamo esplorato insieme le equazioni differenziali del primo ordine, affrontando la teoria e mettendo in pratica le tecniche con esercizi svolti. Spero che questa guida ti sia stata utile e ti abbia fornito gli strumenti necessari per affrontare questo argomento con maggiore sicurezza. Ricorda, la chiave del successo è la pratica costante e la comprensione dei concetti fondamentali. Non avere paura di sperimentare, di fare errori e di imparare da essi.

Quale applicazione pratica delle equazioni differenziali ti incuriosisce di più e vorresti approfondire?