Equazione Della Direttrice Di Una Parabola

Ti sei mai sentito perso nel mondo delle parabole, cercando di capire quel misterioso elemento chiamato "direttrice"? Non preoccuparti, non sei solo! Molti studenti e appassionati di matematica si trovano di fronte a questa sfida. Capire l'equazione della direttrice di una parabola può sembrare ostico all'inizio, ma con un po' di chiarezza e alcuni esempi pratici, diventerà un concetto molto più accessibile. In questo articolo, ti guiderò attraverso il processo, rendendo tutto più semplice e comprensibile.

Cos'è una Parabola e Perché la Direttrice è Importante?

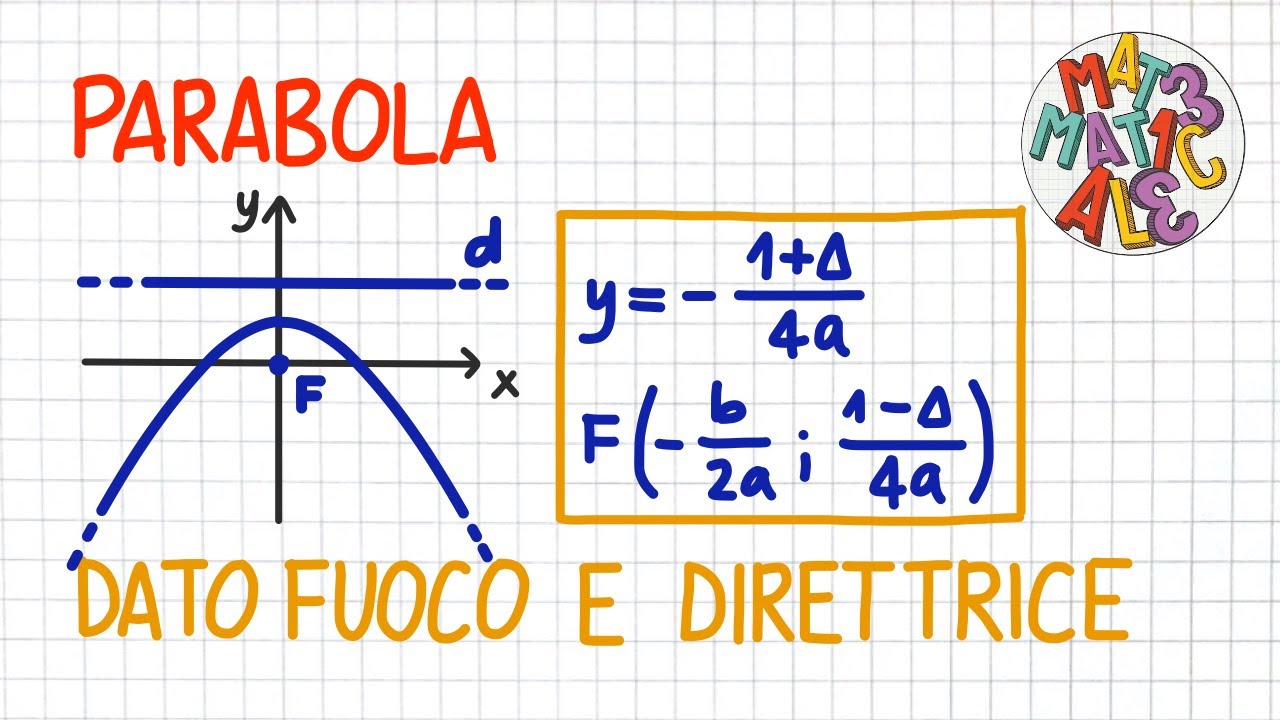
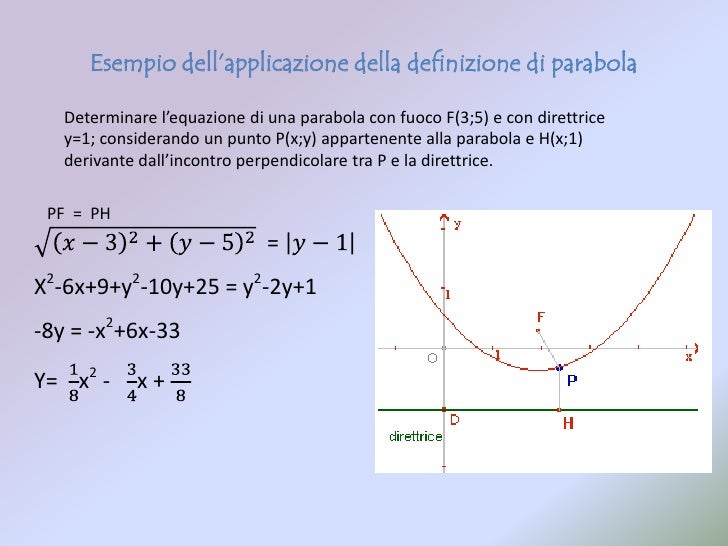
Prima di addentrarci nell'equazione della direttrice, facciamo un breve ripasso su cosa sia una parabola. Una parabola è una curva che si forma quando prendiamo tutti i punti che sono equidistanti da un punto fisso (il fuoco) e da una retta fissa (la direttrice). Immagina di avere una torcia: la forma del fascio luminoso, se proiettato su una superficie piana, assomiglia a una parabola.

La direttrice, quindi, è una retta fondamentale che definisce la forma della parabola. Insieme al fuoco, determina completamente la parabola stessa. Senza la direttrice, non potremmo definire univocamente la parabola. La direttrice è sempre perpendicolare all'asse di simmetria della parabola e si trova dalla parte opposta del fuoco rispetto al vertice. Questa è una regola fondamentale da tenere a mente.

L'Importanza Pratica della Direttrice

Potresti chiederti: "Ok, ma a cosa serve tutto questo nella vita reale?". Le parabole (e quindi le loro direttrici) hanno applicazioni in moltissimi campi:

• Antenne paraboliche: Riflettono le onde radio verso il fuoco, aumentando l'intensità del segnale. La direttrice gioca un ruolo cruciale nel design.
• Fari delle auto: Il filamento è posto nel fuoco di una parabola, e la luce viene riflessa in un fascio parallelo, illuminando la strada.
• Architettura: Le forme paraboliche sono utilizzate per costruire ponti e cupole, offrendo grande resistenza e stabilità.
• Traiettorie di proiettili: In fisica, la traiettoria di un proiettile (ignorando la resistenza dell'aria) è una parabola.

Capire la direttrice, quindi, non è solo un esercizio teorico, ma ti apre le porte a comprendere come funzionano molte delle tecnologie che ci circondano.

L'Equazione della Direttrice: Passo Dopo Passo

Ora, passiamo al cuore della questione: come si trova l'equazione della direttrice? La formula varia a seconda dell'orientamento della parabola (verticale o orizzontale) e della sua posizione nel piano cartesiano.

Parabola con Asse di Simmetria Verticale

Consideriamo la forma più comune: una parabola con asse di simmetria verticale. La sua equazione canonica è:

y = ax² + bx + c

oppure, in forma vertice:

y = a(x - h)² + k

dove (h, k) sono le coordinate del vertice della parabola. Il parametro *a* determina l'apertura e la direzione della parabola (verso l'alto se *a* > 0, verso il basso se *a* < 0).

La distanza tra il vertice e il fuoco (e tra il vertice e la direttrice) è data da:

p = 1 / (4|a|)

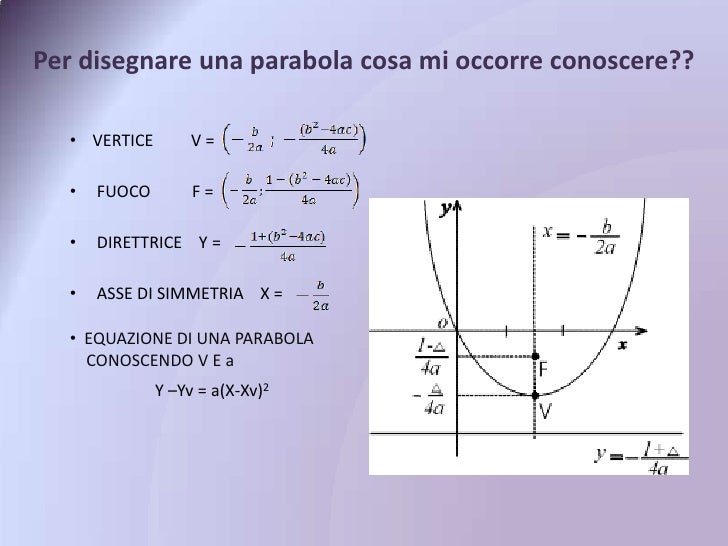
Questa distanza è cruciale! Se la parabola ha asse verticale e vertice in (h, k), l'equazione della direttrice è:

y = k - p

In altre parole, la direttrice è una retta orizzontale che si trova *p* unità sotto il vertice (se *a* > 0) o *p* unità sopra il vertice (se *a* < 0).

Consideriamo la parabola y = 2x². In questo caso, a = 2, b = 0, e c = 0. Il vertice è in (0, 0). La distanza *p* è 1 / (4 * 2) = 1/8. Poiché *a* è positivo, la parabola è rivolta verso l'alto. Quindi, la direttrice si trova 1/8 unità sotto il vertice, e la sua equazione è y = -1/8.

Parabola con Asse di Simmetria Orizzontale

Ora, consideriamo una parabola con asse di simmetria orizzontale. La sua equazione canonica è:

x = ay² + by + c

oppure, in forma vertice:

x = a(y - k)² + h

Anche in questo caso, (h, k) sono le coordinate del vertice. La distanza *p* tra il vertice e il fuoco (e tra il vertice e la direttrice) è sempre:

p = 1 / (4|a|)

Se la parabola ha asse orizzontale e vertice in (h, k), l'equazione della direttrice è:

x = h - p

In questo caso, la direttrice è una retta verticale che si trova *p* unità a sinistra del vertice (se *a* > 0) o *p* unità a destra del vertice (se *a* < 0).

Consideriamo la parabola x = -y². In questo caso, a = -1, b = 0, e c = 0. Il vertice è in (0, 0). La distanza *p* è 1 / (4 * 1) = 1/4. Poiché *a* è negativo, la parabola è rivolta verso sinistra. Quindi, la direttrice si trova 1/4 unità a destra del vertice, e la sua equazione è x = 1/4.

Consigli Pratici per Trovare l'Equazione della Direttrice

Ecco alcuni consigli utili per affrontare questo tipo di problemi:

1. Identifica la forma dell'equazione: Determina se la parabola ha asse verticale o orizzontale. Questo ti guiderà nella scelta della formula corretta.
2. Trova il vertice: Se l'equazione è in forma canonica, potresti dover completare il quadrato per trovare le coordinate del vertice (h, k). Ricorda che il vertice è un punto cruciale per determinare la posizione della direttrice.
3. Calcola la distanza *p*: Utilizza la formula p = 1 / (4|a|). Il valore assoluto di *a* è importante perché *p* rappresenta una distanza, che è sempre positiva.
4. Applica la formula corretta: A seconda dell'orientamento della parabola, utilizza la formula appropriata (y = k - p per l'asse verticale, x = h - p per l'asse orizzontale).
5. Visualizza la parabola: Un piccolo schizzo può aiutarti a visualizzare la posizione della direttrice rispetto al vertice e al fuoco.

Esercizi e Risorse Utili

La pratica rende perfetti! Prova a risolvere diversi esercizi per familiarizzare con le formule e i concetti. Puoi trovare esercizi online e nei libri di testo di matematica. Inoltre, esistono numerosi strumenti online che ti permettono di disegnare parabole e visualizzare la direttrice.

Alcune risorse utili includono:

• Khan Academy: Offre lezioni gratuite e esercizi sulla geometria analitica, inclusi i concetti relativi alle parabole.
• GeoGebra: Un software gratuito di geometria dinamica che ti permette di disegnare parabole e visualizzare la direttrice.
• WolframAlpha: Un potente motore di ricerca computazionale che può aiutarti a risolvere equazioni e visualizzare grafici.

Conclusione

Spero che questo articolo ti abbia aiutato a demistificare l'equazione della direttrice di una parabola. Ricorda, la chiave è capire i concetti fondamentali e fare tanta pratica. Non scoraggiarti se incontri difficoltà, la matematica richiede tempo e pazienza. Con un po' di impegno, sarai in grado di padroneggiare questo argomento e applicarlo a una vasta gamma di problemi reali. Buono studio!