Equazione Della Bisettrice Del Primo E Terzo Quadrante

Ciao! Se ti sei mai trovato a fissare un grafico cartesiano, chiedendoti come descrivere matematicamente quella linea perfetta che divide esattamente in due il primo e il terzo quadrante, sei nel posto giusto. Molti studenti di matematica (e non solo!) si trovano di fronte a questa domanda. La buona notizia è che è più semplice di quanto sembri! In questo articolo, esploreremo l'equazione della bisettrice del primo e terzo quadrante in modo chiaro e accessibile, spiegando perché è così importante e come si applica nella pratica.

Che cos'è la Bisettrice?

Prima di addentrarci nell'equazione specifica, definiamo cos'è una bisettrice in generale. Immagina un angolo. La bisettrice è semplicemente una linea che divide quell'angolo in due angoli uguali. Nel caso del piano cartesiano, la bisettrice del primo e terzo quadrante divide l'angolo formato dagli assi x e y positivi, e gli assi x e y negativi, in due parti uguali di 45 gradi ciascuna.

Perché è importante? La bisettrice non è solo una linea teorica. Compare in molti contesti matematici e fisici, dalla geometria analitica all'ottica. Capire la sua equazione ci permette di manipolarla e utilizzarla per risolvere problemi complessi.

L'Equazione Fondamentale: y = x

Ecco la risposta: l'equazione della bisettrice del primo e terzo quadrante è semplicemente:

y = x

Sembra troppo semplice per essere vero? Analizziamo perché funziona.

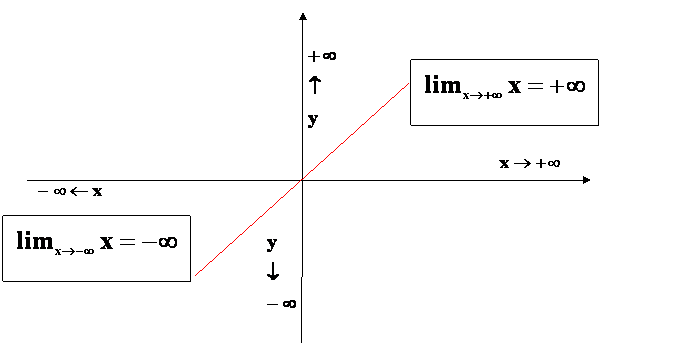
Questa equazione significa che per ogni punto sulla linea, il valore della coordinata y è esattamente uguale al valore della coordinata x. Quindi, se x è 2, y è 2. Se x è -3, y è -3. Questo crea una linea retta che parte dall'origine (0,0) e si estende attraverso il primo e il terzo quadrante, dividendo perfettamente l'angolo retto in due.

Visualizziamolo:

• Pensa al punto (1, 1). Soddisfa l'equazione y = x.
• Pensa al punto (-2, -2). Anche questo soddisfa l'equazione y = x.
• Prova con qualsiasi numero! Vedrai che la relazione y = x è sempre vera per i punti sulla bisettrice.

Perché non altre equazioni?

Potresti chiederti: "Perché non un'equazione più complessa?". La bellezza di y = x sta nella sua semplicità ed efficacia. Qualsiasi altra equazione lineare con una pendenza diversa da 1 (o un'intercetta diversa da 0) non dividerebbe l'angolo in modo uniforme. Per esempio, l'equazione y = 2x creerebbe una linea più ripida, mentre y = x + 1 sposterebbe la linea verso l'alto, non passando per l'origine.

Applicazioni Pratiche

Ora che conosciamo l'equazione, vediamo come viene utilizzata in diverse aree:

• Grafica di funzioni: La bisettrice y = x è spesso usata come riferimento quando si graficano altre funzioni. Può aiutare a visualizzare come una funzione si comporta rispetto all'identità (dove l'output è uguale all'input).
• Trasformazioni geometriche: La bisettrice può essere usata come asse di riflessione per trasformare figure geometriche.
• Analisi dei dati: In statistica, la bisettrice può essere usata per confrontare due insiemi di dati. Se i punti si raggruppano attorno alla bisettrice, suggerisce una forte correlazione tra i due insiemi di dati.
• Informatica grafica: L'equazione y = x è fondamentale per la creazione di immagini e animazioni al computer, specialmente in contesti dove è necessaria una simmetria o una proporzionalità diretta.
• Ottica: In ottica geometrica, la bisettrice del primo e terzo quadrante può rappresentare la direzione di un raggio di luce dopo una riflessione speculare, specialmente se il sistema è allineato in modo tale che la normale alla superficie riflettente coincida con l'asse y.

Affrontare i Controverti (Sebbene Siano Rari)

È difficile trovare veri e propri "controverti" all'equazione della bisettrice. Tuttavia, è importante considerare che la bisettrice specifica di cui stiamo parlando si riferisce solo al primo e terzo quadrante. Esistono altre bisettrici! Ad esempio:

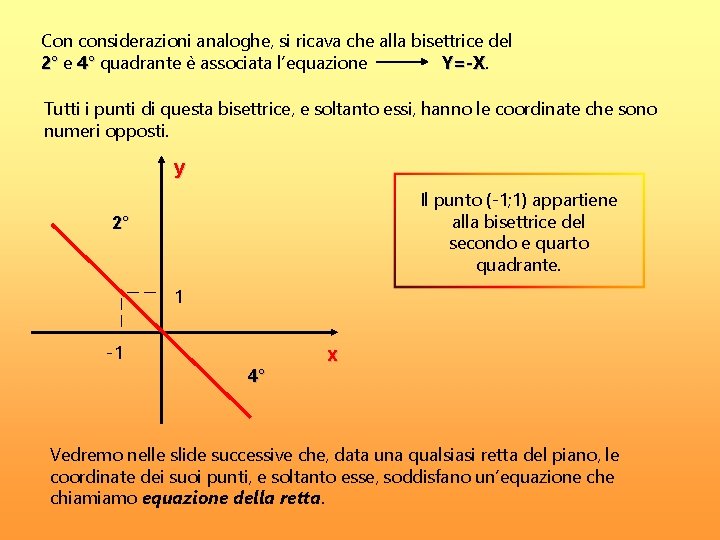
• La bisettrice del secondo e quarto quadrante: Questa linea ha equazione y = -x. Dividete l'angolo formato dall'asse y positivo e l'asse x negativo in due parti uguali.
• Bisettrice di angoli diversi da quelli formati dagli assi cartesiani: In questo caso, l'equazione della bisettrice sarà più complessa e richiederà la conoscenza dell'angolo di partenza.

Quindi, è essenziale specificare a quale bisettrice ci si riferisce per evitare ambiguità.

Un Esempio Concreto

Immagina di avere un robot che deve muoversi in diagonale attraverso una stanza. Se la stanza è rappresentata da un piano cartesiano e il robot parte dall'origine, la sua traiettoria ideale per muoversi in diagonale (mantenendo la stessa distanza dagli assi x e y) seguirà la bisettrice del primo e terzo quadrante. In questo caso, controllare il robot per assicurarsi che le sue coordinate x e y siano sempre uguali (y = x) garantirà che si muova in modo efficiente in diagonale.

Oltre l'Equazione: L'Importanza del Concetto

Anche se l'equazione y = x è fondamentale, è ancora più importante capire il concetto di bisettrice. Capire che rappresenta una linea di simmetria, una linea che divide un angolo in due parti uguali, ti aiuterà a risolvere problemi più complessi e ad applicare questo concetto in contesti diversi.

Pensa alla bisettrice come a uno specchio: Ogni punto da una parte della linea ha un'immagine speculare dall'altra parte, mantenendo la stessa distanza dalla linea.

Riepilogo

Ricapitoliamo i punti chiave:

• L'equazione della bisettrice del primo e terzo quadrante è y = x.
• Questo significa che per ogni punto sulla linea, le coordinate x e y sono uguali.
• La bisettrice divide l'angolo formato dagli assi x e y positivi (e negativi) in due parti uguali.
• Ha molte applicazioni in matematica, fisica, informatica e altre aree.
• È importante specificare a quale bisettrice ci si riferisce per evitare confusione.

La bisettrice del primo e terzo quadrante è un concetto semplice ma potente. Spero che questo articolo ti abbia aiutato a capire meglio la sua equazione e le sue applicazioni. Ricorda, la matematica è come un linguaggio: più la pratichi, più fluente diventi!

Ora, prova questo: disegna un piano cartesiano e traccia la linea y = x. Poi, scegli alcuni punti a caso e verifica se soddisfano l'equazione. Come potresti usare questa retta per creare un'immagine simmetrica? Cosa accadrebbe se moltiplicassi l'equazione per un numero, ad esempio y=2x? Cosa cambierebbe sul grafico?