Distanza In Km Tra Due Punti

Calcolare la distanza tra due punti è un problema fondamentale in molti campi, dalla navigazione alla geometria, dalla programmazione di videogiochi alla logistica. Comprendere i metodi per determinare questa distanza è essenziale per risolvere problemi pratici e teorici. Questo articolo esplorerà i diversi approcci per calcolare la distanza in chilometri tra due punti, considerando sia coordinate geografiche su una superficie curva (la Terra) che coordinate cartesiane su un piano.

Concetti Fondamentali

Prima di addentrarci nei metodi di calcolo, è cruciale definire alcuni concetti chiave:

• Coordinate Geografiche: Latitudine e longitudine che specificano la posizione di un punto sulla superficie terrestre. La latitudine indica la distanza angolare dal piano equatoriale (Nord o Sud), mentre la longitudine indica la distanza angolare dal meridiano di Greenwich (Est o Ovest).
• Coordinate Cartesiane: Un sistema di coordinate che utilizza assi perpendicolari (x, y) per definire la posizione di un punto in un piano, o assi (x, y, z) per definire la posizione di un punto nello spazio tridimensionale.
• Superficie Terrestre: La Terra non è una sfera perfetta, ma un geoide. Tuttavia, per semplificare i calcoli, spesso viene approssimata a una sfera o un ellissoide.

Distanza Euclidea: Un Approccio Semplice

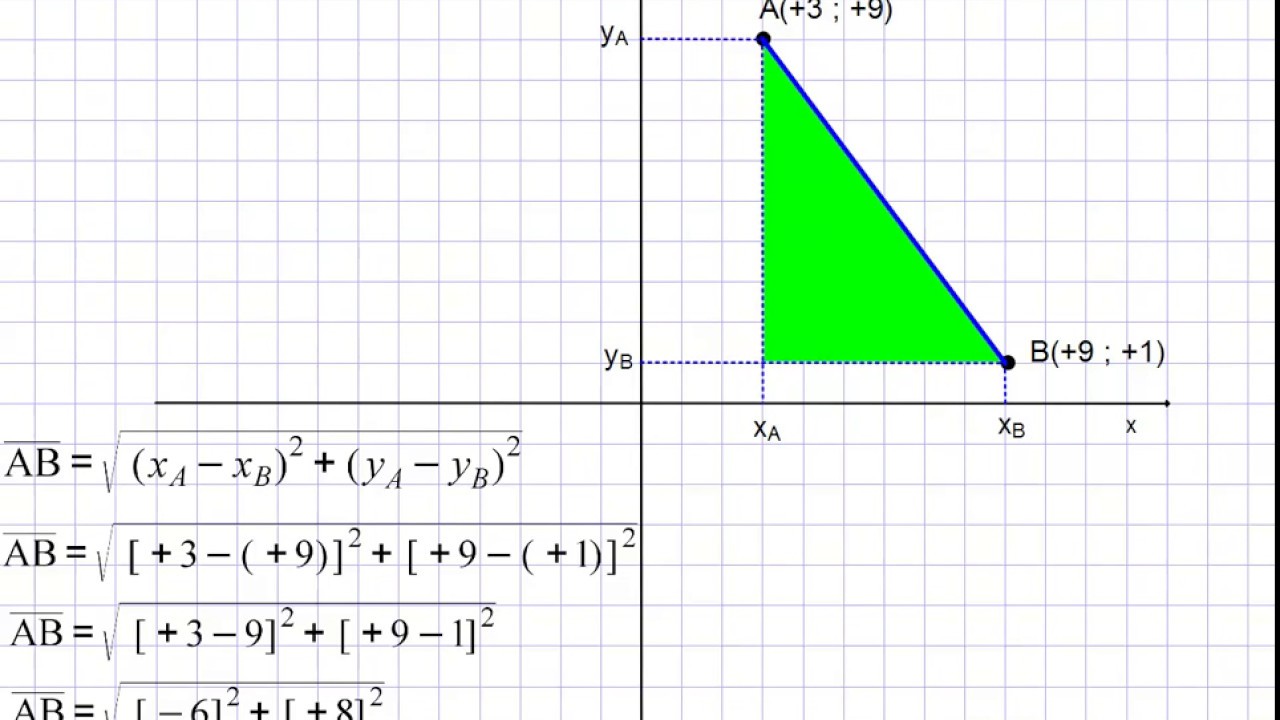
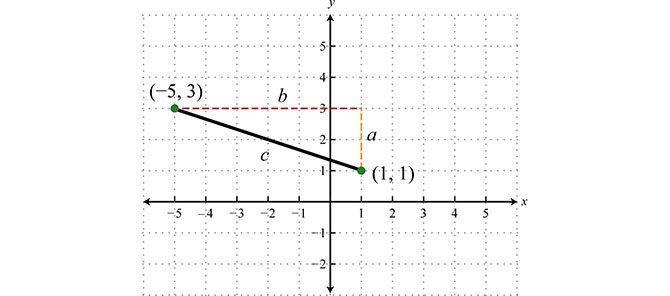
Il metodo più semplice per calcolare la distanza tra due punti è utilizzare la distanza euclidea. Questo approccio è valido quando si considerano coordinate cartesiane e si assume che lo spazio sia piano. La formula è derivata dal teorema di Pitagora.

Se abbiamo due punti P1(x1, y1) e P2(x2, y2) in un piano cartesiano, la distanza euclidea d tra di essi è data da:

d = √((x2 - x1)² + (y2 - y1)²)

Nel caso di coordinate tridimensionali (x, y, z), la formula diventa:

d = √((x2 - x1)² + (y2 - y1)² + (z2 - z1)²)

Esempio: Consideriamo due punti in un piano: A(1, 2) e B(4, 6). La distanza euclidea tra A e B è:

d = √((4 - 1)² + (6 - 2)²) = √((3)² + (4)²) = √(9 + 16) = √25 = 5

Questo metodo è rapido e facile da implementare, ma è preciso solo su brevi distanze e in aree dove la curvatura terrestre può essere ignorata.

La Formula di Haversine: Distanza sulla Sfera

Quando si calcolano distanze tra punti sulla superficie terrestre, che è approssimativamente sferica, la distanza euclidea non è accurata. È necessario utilizzare formule che tengano conto della curvatura terrestre. La formula di Haversine è un metodo ampiamente utilizzato per calcolare la distanza "as the crow flies" tra due punti sulla superficie di una sfera, dati la loro latitudine e longitudine.

Siano (lat1, lon1) e (lat2, lon2) le coordinate geografiche dei due punti, espresse in radianti. La formula di Haversine è:

a = sin²(Δlat/2) + cos(lat1) * cos(lat2) * sin²(Δlon/2)

c = 2 * atan2(√a, √(1-a))

d = R * c

Dove:

• Δlat = lat2 - lat1 (differenza di latitudine)
• Δlon = lon2 - lon1 (differenza di longitudine)
• R è il raggio della Terra (approssimativamente 6371 km)
• atan2 è la funzione arcotangente a due argomenti (utile per determinare il quadrante corretto).

La distanza d risultante è in chilometri.

Esempio: Calcoliamo la distanza tra Roma (41.9028° N, 12.4964° E) e Parigi (48.8566° N, 2.3522° E). Dobbiamo prima convertire le coordinate in radianti:

lat1 = 41.9028 * (π / 180) ≈ 0.7312 rad

lon1 = 12.4964 * (π / 180) ≈ 0.2181 rad

lat2 = 48.8566 * (π / 180) ≈ 0.8527 rad

lon2 = 2.3522 * (π / 180) ≈ 0.0410 rad

Applicando la formula di Haversine (con R = 6371 km), otteniamo una distanza di circa 1105 km.

La formula di Haversine è generalmente accurata per la maggior parte delle applicazioni, ma può presentare lievi errori, specialmente per distanze molto lunghe, a causa dell'approssimazione sferica della Terra.

Distanza Ortodromica (Great-Circle Distance): Ancora Più Precisione

La distanza ortodromica, nota anche come "great-circle distance", è la distanza più breve tra due punti sulla superficie di una sfera. È calcolata lungo un cerchio massimo (un cerchio sulla sfera il cui centro coincide con il centro della sfera). Questa distanza è sempre minore o uguale alla distanza calcolata con la formula di Haversine (anche se, in pratica, la differenza è spesso minima).

La formula per calcolare la distanza ortodromica è:

d = R * arccos(sin(lat1) * sin(lat2) + cos(lat1) * cos(lat2) * cos(lon2 - lon1))

Dove:

• lat1, lon1 e lat2, lon2 sono le coordinate geografiche dei due punti in radianti.
• R è il raggio della Terra (approssimativamente 6371 km).
• arccos è la funzione arcocoseno.

Esempio: Utilizzando le stesse coordinate di Roma e Parigi dell'esempio precedente, applichiamo la formula della distanza ortodromica. La distanza calcolata sarà molto simile a quella ottenuta con la formula di Haversine, circa 1105 km.

La distanza ortodromica è più precisa della formula di Haversine, soprattutto per distanze molto lunghe, ma la differenza in pratica è spesso trascurabile per la maggior parte delle applicazioni.

Considerazioni Aggiuntive e Strumenti

È importante notare che queste formule considerano la Terra come una sfera perfetta. In realtà, la Terra è un geoide, più precisamente approssimabile con un ellissoide. Per calcoli ancora più precisi, soprattutto in applicazioni geodetiche, si utilizzano modelli più complessi e software specializzati che tengono conto della forma ellissoidale della Terra.

Esistono numerosi strumenti online e librerie software che semplificano il calcolo delle distanze tra punti geografici. Ad esempio, molte API di mappatura (come Google Maps API o Leaflet) forniscono funzioni per calcolare distanze utilizzando diversi metodi. Le librerie di programmazione in linguaggi come Python (ad esempio, la libreria `geopy`) offrono funzionalità simili.

Esempi Reali e Dati

Vediamo alcuni esempi reali di come il calcolo della distanza tra due punti è utilizzato in vari contesti:

• Navigazione Aerea: I sistemi di navigazione aerea utilizzano la distanza ortodromica per pianificare le rotte di volo più brevi tra due aeroporti.
• Logistica e Trasporti: Le aziende di logistica calcolano le distanze tra magazzini e destinazioni per ottimizzare i percorsi di consegna e ridurre i costi di trasporto.
• Applicazioni di Mappe: Le app di mappe (come Google Maps, Apple Maps) calcolano le distanze tra la posizione dell'utente e i punti di interesse per fornire indicazioni stradali e informazioni sulla distanza.
• Programmazione di Videogiochi: Nei videogiochi open-world, il calcolo della distanza tra personaggi o oggetti è fondamentale per la gestione dell'intelligenza artificiale e per l'interazione tra gli elementi del gioco.
• Astronomia: Il calcolo delle distanze tra corpi celesti è essenziale per comprendere la struttura e l'evoluzione dell'universo.

Dati: Un esempio di dati reali che evidenziano l'importanza del calcolo accurato delle distanze è il sistema GPS (Global Positioning System). Il GPS utilizza una rete di satelliti per determinare la posizione di un ricevitore sulla Terra. La precisione del GPS dipende in gran parte dalla capacità di calcolare con precisione le distanze tra il ricevitore e i satelliti, tenendo conto degli effetti relativistici e della forma non sferica della Terra.

Conclusioni

Il calcolo della distanza tra due punti è un problema fondamentale con applicazioni innumerevoli. La scelta del metodo appropriato dipende dalla precisione richiesta e dalla scala del problema. Per distanze brevi su un piano, la distanza euclidea è sufficiente. Per distanze significative sulla superficie terrestre, è necessario utilizzare la formula di Haversine o la distanza ortodromica. Per applicazioni che richiedono la massima precisione, si utilizzano modelli geodetici più complessi.

Comprendere i principi alla base di questi calcoli è essenziale per chiunque lavori in campi come la navigazione, la logistica, la cartografia o la programmazione di applicazioni geografiche. Sperimenta con le formule e gli strumenti presentati in questo articolo per acquisire una comprensione pratica del calcolo della distanza tra due punti!