Differenza Tra Sottoinsieme E Sottoinsieme Proprio

Capita spesso, quando ci si avvicina alla matematica, di imbattersi in concetti che, pur apparentemente simili, nascondono sottili ma fondamentali differenze. Uno di questi è proprio la distinzione tra sottoinsieme e sottoinsieme proprio. Non fraintendere, non sei il solo a sentirti un po' confuso! Molti studenti, e a volte anche professionisti non direttamente coinvolti con la teoria degli insiemi, trovano queste definizioni ostiche. Cerchiamo quindi di fare chiarezza, partendo dalle basi e arrivando a comprendere l'importanza di questa distinzione.
Perché è importante capire la differenza tra sottoinsieme e sottoinsieme proprio? Pensa ad un programmatore che deve validare dei dati. Se non capisce bene le relazioni tra gli insiemi di dati che manipola, rischia di introdurre bug nel codice. Immagina un analista di mercato che vuole segmentare i suoi clienti: una comprensione errata di questi concetti potrebbe portare a conclusioni sbagliate sulla sua clientela. In definitiva, una solida base in teoria degli insiemi è essenziale per un pensiero logico e rigoroso, applicabile in moltissimi campi.
Cos'è un Insieme? Un Ripasso Veloce
Prima di affrontare i sottoinsiemi, è fondamentale capire cos'è un insieme. In parole semplici, un insieme è una collezione di oggetti distinti, chiamati elementi. Questi elementi possono essere numeri, lettere, persone, o qualsiasi altra cosa. L'importante è che siano ben definiti e distinguibili gli uni dagli altri. Ad esempio, l'insieme delle vocali dell'alfabeto italiano è {a, e, i, o, u}.
Un insieme si rappresenta solitamente con parentesi graffe {}. L'ordine degli elementi all'interno dell'insieme non conta e non ci possono essere elementi duplicati.
Il Concetto di Sottoinsieme
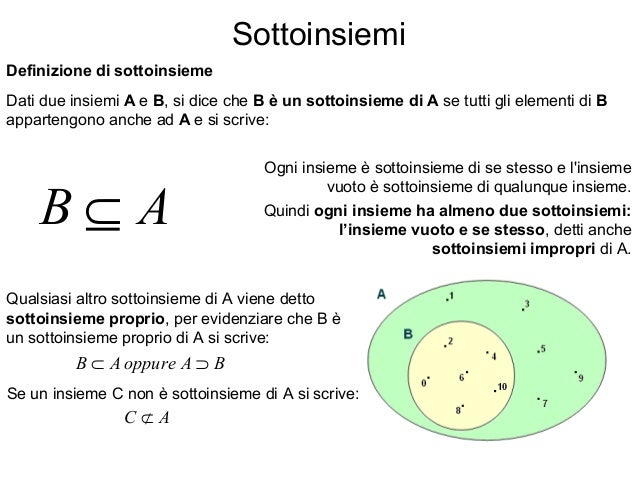
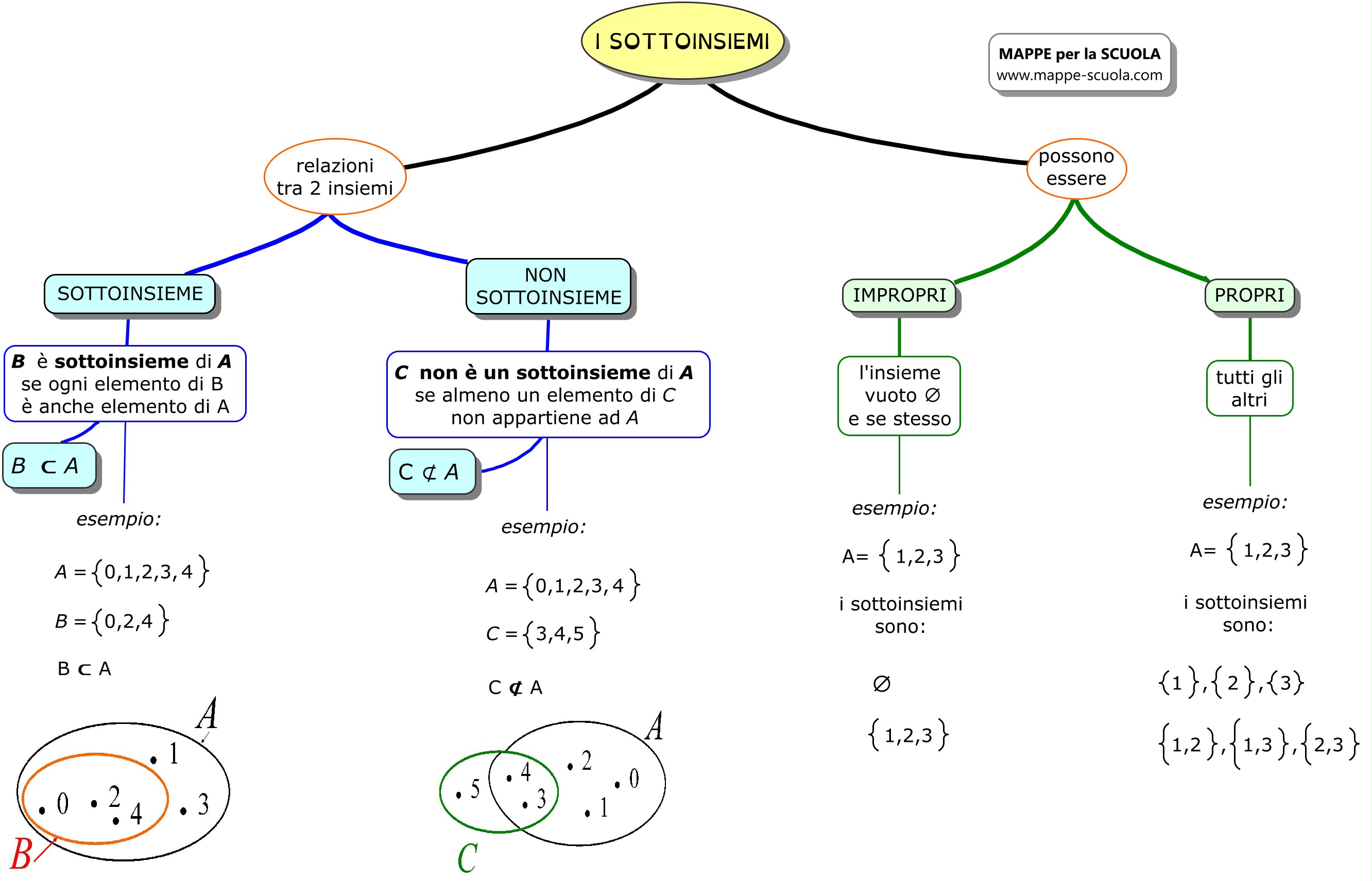
Ora che abbiamo rinfrescato la definizione di insieme, possiamo affrontare il concetto di sottoinsieme. Un insieme A è un sottoinsieme di un insieme B se tutti gli elementi di A appartengono anche a B. In altre parole, se prendi qualsiasi elemento di A, lo troverai sicuramente anche in B.
La notazione matematica per indicare che A è un sottoinsieme di B è: A ⊆ B.
Facciamo un esempio concreto:
- Sia B l'insieme di tutti i numeri pari minori di 10: B = {2, 4, 6, 8}.
- Sia A l'insieme {2, 4}.
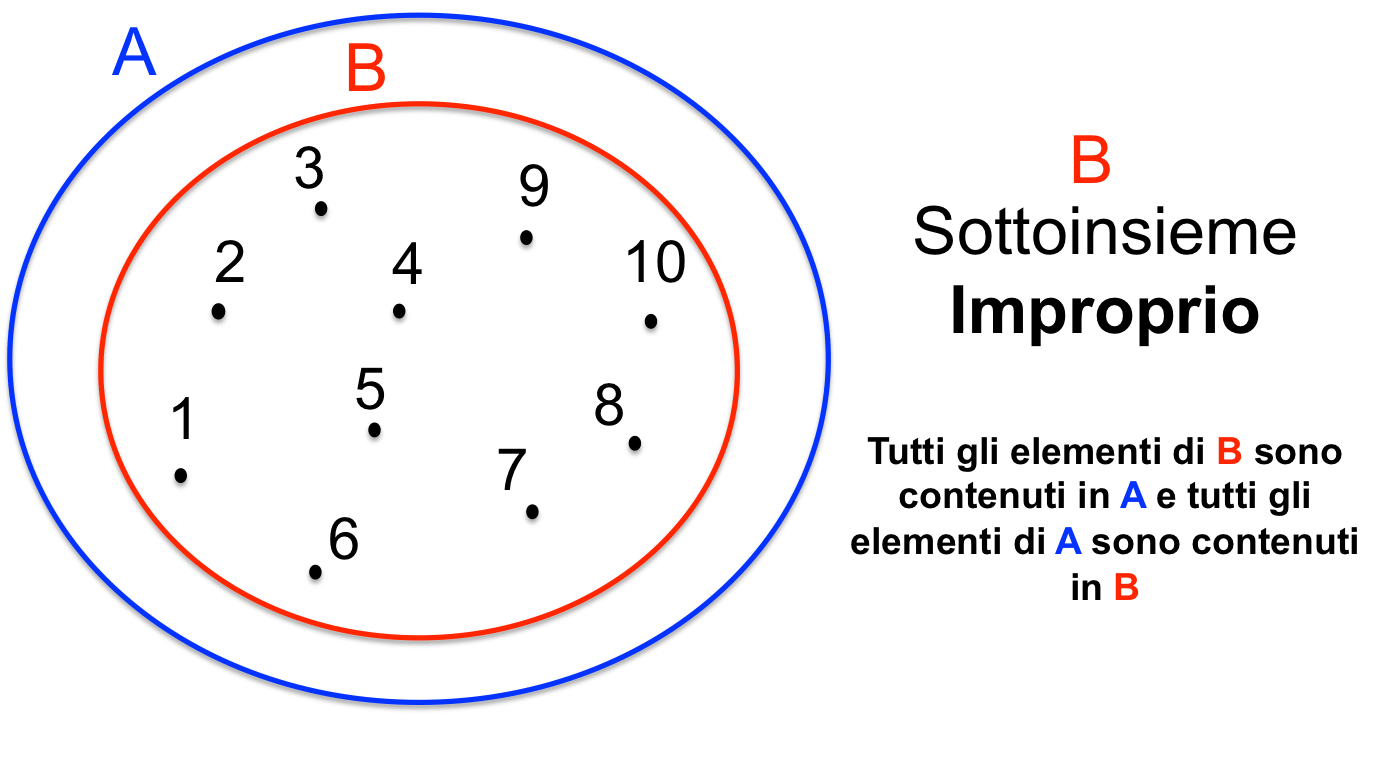
Attenzione! Un insieme è sempre sottoinsieme di se stesso. Nel nostro esempio, l'insieme B = {2, 4, 6, 8} è un sottoinsieme di se stesso, ovvero B ⊆ B.
L'insieme vuoto (indicato con il simbolo Ø) è considerato un sottoinsieme di qualsiasi insieme. Questo può sembrare strano, ma è una convenzione matematica utile e coerente con le definizioni. Possiamo dire che Ø ⊆ B per qualsiasi insieme B.
Il Sottoinsieme Proprio: La Differenza Chiave
Ed eccoci al punto cruciale: il sottoinsieme proprio. Un insieme A è un sottoinsieme proprio di un insieme B se A è un sottoinsieme di B e A non è uguale a B. In altre parole, tutti gli elementi di A appartengono a B, ma B contiene almeno un elemento che non appartiene ad A.
La notazione matematica per indicare che A è un sottoinsieme proprio di B è: A ⊂ B.
Torniamo al nostro esempio precedente:
- B = {2, 4, 6, 8}
- A = {2, 4}
Se considerassimo invece l'insieme C = {2, 4, 6, 8}, allora C sarebbe un sottoinsieme di B (C ⊆ B), ma non un sottoinsieme proprio, perché C è uguale a B.
Riassumendo le Differenze:
- Sottoinsieme (⊆): Tutti gli elementi di A appartengono a B. A può essere uguale a B.
- Sottoinsieme Proprio (⊂): Tutti gli elementi di A appartengono a B. A non può essere uguale a B. B deve contenere almeno un elemento non presente in A.
Perché questa Distinzione è Importante?
La distinzione tra sottoinsieme e sottoinsieme proprio non è solo un cavillo matematico. È fondamentale per evitare ambiguità e per esprimere concetti con precisione. In molti contesti, si vuole escludere la possibilità che due insiemi siano uguali. Ad esempio, quando si parla di sottoalberi in un albero binario, si intende solitamente che il sottoalbero sia più piccolo dell'albero originale. In questo caso, si usa il concetto di sottoinsieme proprio.
Consideriamo un altro esempio: Immagina di avere un database di clienti. Vuoi creare dei segmenti di clienti basati su determinate caratteristiche (età, sesso, interessi, ecc.). Se crei un segmento che contiene tutti i clienti del database, non hai fatto una vera segmentazione. Hai solo l'insieme originale dei clienti. Una segmentazione efficace richiede la creazione di sottoinsiemi propri del database, ovvero gruppi di clienti con caratteristiche specifiche che li distinguono dal resto.
Controargomentazioni: Non è Sempre Così Importante!
È vero, in alcuni contesti, la distinzione tra sottoinsieme e sottoinsieme proprio non è cruciale. Ad esempio, in alcuni linguaggi di programmazione, la nozione di "subset" può essere usata in modo generico, senza fare una distinzione formale tra i due concetti. Tuttavia, è importante conoscere la differenza, perché quando la precisione è fondamentale, l'utilizzo corretto della terminologia è essenziale per evitare errori di interpretazione.
Inoltre, anche se in un determinato contesto la distinzione non è direttamente rilevante, la comprensione dei concetti sottostanti (inclusione, uguaglianza, cardinalità) è sempre utile per ragionare in modo logico e strutturato.
Come Ricordare la Differenza? Un Trucco Mnemonico
Un modo semplice per ricordare la differenza è pensare al simbolo:
- ⊆ (sottoinsieme): La linea sotto il simbolo indica che l'uguaglianza è possibile.
- ⊂ (sottoinsieme proprio): Non c'è la linea sotto, quindi l'uguaglianza è esclusa.
In Pratica: Esercizi e Approfondimenti
Il modo migliore per comprendere appieno la differenza tra sottoinsieme e sottoinsieme proprio è fare pratica con degli esercizi. Prova a creare degli insiemi di esempio e a identificare i loro sottoinsiemi e sottoinsiemi propri. Puoi anche cercare esercizi online o consultare un libro di testo di teoria degli insiemi.
Ecco alcuni spunti per ulteriori approfondimenti:
- Diagrammi di Venn: Utilizza i diagrammi di Venn per visualizzare le relazioni tra gli insiemi. Questo può aiutarti a comprendere meglio i concetti di inclusione e intersezione.
- Cardinalità di un insieme: La cardinalità di un insieme è il numero di elementi che contiene. La cardinalità di un sottoinsieme proprio è sempre minore della cardinalità dell'insieme originale.
- Teoria degli insiemi assiomatica: Approfondisci i fondamenti assiomatici della teoria degli insiemi per una comprensione ancora più rigorosa.
Ricorda, la matematica è come un linguaggio: più la pratichi, più diventi fluente. Non scoraggiarti di fronte alle difficoltà, ma affronta ogni sfida con curiosità e determinazione!
Speriamo che questa spiegazione ti sia stata utile. Hai altri dubbi o domande sulla teoria degli insiemi? C'è qualche altro concetto che ti sembra particolarmente ostico?