Derivata Di E Alla Meno X

Capita a tutti noi, prima o poi, di trovarci di fronte a concetti matematici che sembrano ostacoli insormontabili. La derivata di e alla meno x, ovvero d/dx (e^-x), è uno di questi per molti studenti e professionisti. Ma non temete! Questo articolo è pensato proprio per voi, per rendere questo argomento accessibile e comprensibile, mostrando come questo concetto, apparentemente astratto, si manifesta concretamente nel mondo che ci circonda.

Perché Dovremmo Preoccuparci di d/dx (e^-x)?

Potreste chiedervi: perché dovrei imparare a derivare una funzione esponenziale negativa? La risposta è che e^-x e le sue derivate compaiono in una miriade di applicazioni pratiche, che spaziano dalla fisica alla finanza, passando per l'ingegneria e la biologia.

Ecco alcuni esempi concreti:

Decadimento Radioattivo: La quantità di una sostanza radioattiva che decade nel tempo segue una legge esponenziale negativa. Comprendere la derivata di e^-x ci permette di calcolare la velocità di decadimento.
Circuiti Elettrici: La scarica di un condensatore in un circuito RC (resistenza-capacità) è descritta da una funzione esponenziale negativa. La derivata ci aiuta a determinare la corrente che scorre nel circuito nel tempo.
Diffusione di Farmaci: La concentrazione di un farmaco nel sangue diminuisce nel tempo secondo una legge esponenziale negativa. La derivata ci consente di modellare e prevedere la velocità di eliminazione del farmaco.
Processi di Raffreddamento: La velocità con cui un oggetto si raffredda è proporzionale alla differenza di temperatura tra l'oggetto e l'ambiente circostante, e può essere modellata con una funzione esponenziale negativa.
Finanza: In alcuni modelli finanziari, il valore di un asset può diminuire esponenzialmente nel tempo, e la derivata ci permette di calcolare la velocità di tale diminuzione.

La Derivata di e^x: Un Richiamo Essenziale

Prima di affrontare e^-x, è fondamentale ricordare la derivata della funzione esponenziale di base, e^x. La derivata di e^x è semplicemente... e^x! Questo è un risultato fondamentale da tenere a mente, poiché ci servirà come base per derivare e^-x.

Matematicamente:

d/dx (e^x) = e^x

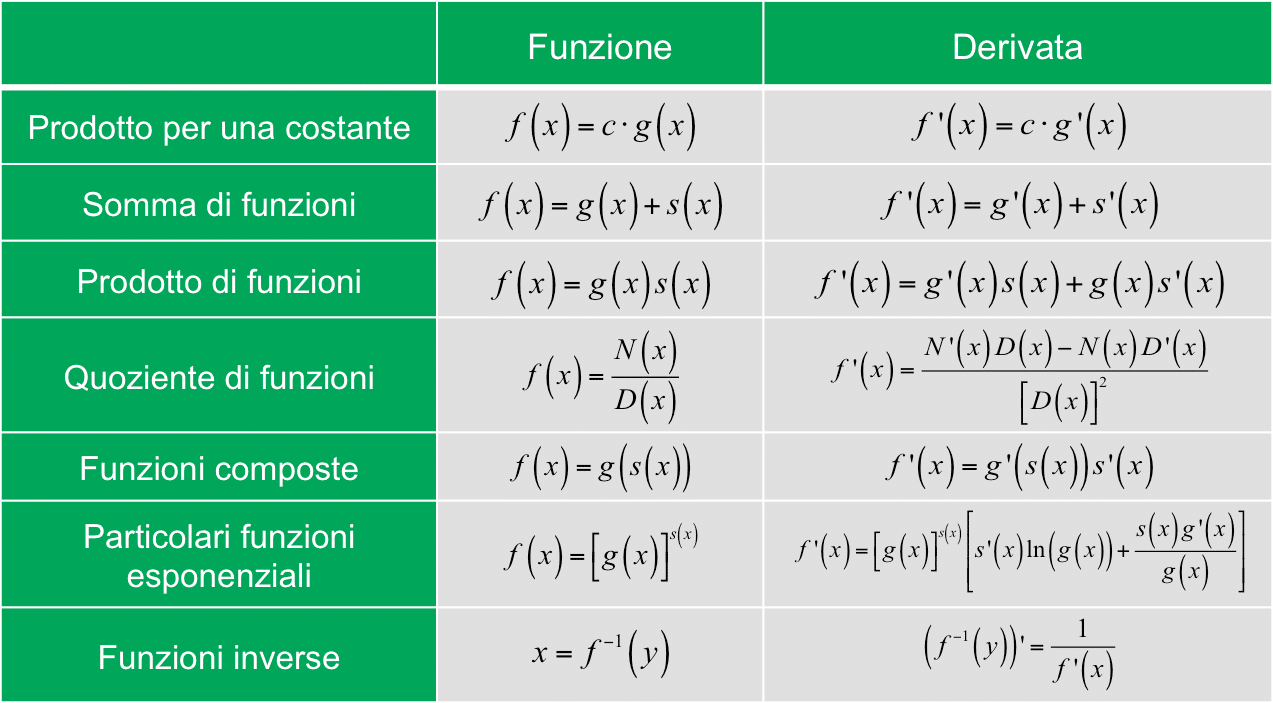
La Regola della Catena: L'Ingrediente Chiave

La derivata di e^-x richiede l'applicazione della regola della catena. Questa regola è uno strumento potente che ci permette di derivare funzioni composte, ovvero funzioni all'interno di altre funzioni. In questo caso, abbiamo la funzione esponenziale e^u, dove u = -x.

La regola della catena afferma che:

d/dx [f(g(x))] = f'(g(x)) * g'(x)

In parole semplici, deriviamo la funzione esterna (f) valutata nella funzione interna (g(x)) e poi moltiplichiamo per la derivata della funzione interna (g'(x)).

Derivando e^-x Passo Dopo Passo

Applichiamo ora la regola della catena a e^-x:

Identifichiamo le funzioni:
- Funzione esterna: f(u) = e^u
- Funzione interna: g(x) = -x
Calcoliamo le derivate:
- f'(u) = d/du (e^u) = e^u
- g'(x) = d/dx (-x) = -1
Applichiamo la regola della catena:
- d/dx (e^-x) = f'(g(x)) * g'(x) = e^-x * (-1) = -e^-x

Pertanto, la derivata di e^-x è -e^-x.

In sintesi:

d/dx (e^-x) = -e^-x

Un Esempio Pratico: Decadimento Radioattivo

Immaginiamo di avere una sostanza radioattiva la cui quantità N(t) al tempo t è data da:

N(t) = N₀ * e^-λt

dove N₀ è la quantità iniziale della sostanza e λ (lambda) è la costante di decadimento.

Per trovare la velocità di decadimento, dobbiamo derivare N(t) rispetto a t:

dN/dt = d/dt (N₀ * e^-λt)

Usando la regola della catena (e ricordando che N₀ è una costante), otteniamo:

dN/dt = N₀ * (-λ) * e^-λt = -λN₀e^-λt = -λN(t)

Questo risultato ci dice che la velocità di decadimento è proporzionale alla quantità di sostanza radioattiva presente e alla costante di decadimento. Il segno negativo indica che la quantità di sostanza sta diminuendo nel tempo.

Contro-argomentazioni e Chiarimenti

Alcuni potrebbero pensare che derivare e^-x sia un processo complesso e che esistano metodi più semplici. In realtà, la regola della catena è lo strumento più diretto e concettualmente chiaro per affrontare questo tipo di derivata. Altre tecniche, come l'uso di serie di Taylor, possono essere utilizzate, ma spesso risultano più complicate e meno intuitive.

Un altro punto di confusione potrebbe derivare dalla somiglianza tra e^x e e^-x. È fondamentale ricordare che la derivata di e^x è e^x, mentre la derivata di e^-x è -e^-x. Il segno meno è cruciale e deriva dall'applicazione della regola della catena.

Consigli per Padronizzare la Derivata di e^-x

Ecco alcuni suggerimenti per migliorare la vostra comprensione e abilità nel derivare e^-x:

Esercitatevi Regolarmente: La pratica rende perfetti! Risolvete numerosi esercizi che coinvolgono la derivata di e^-x in diversi contesti.
Comprendete la Regola della Catena: Assicuratevi di avere una solida comprensione della regola della catena e di come applicarla correttamente.
Visualizzate la Funzione: Cercate di visualizzare graficamente la funzione e^-x e la sua derivata. Questo vi aiuterà a comprendere meglio il comportamento della funzione e la sua velocità di variazione.
Utilizzate Risorse Online: Esistono numerose risorse online, come tutorial, video e calcolatrici di derivate, che possono aiutarvi a chiarire dubbi e a risolvere esercizi.
Chiedete Aiuto: Non abbiate paura di chiedere aiuto a insegnanti, tutor o compagni di studio se incontrate difficoltà.

Conclusione: Un Passo Avanti nella Matematica

Speriamo che questo articolo vi abbia fornito una comprensione chiara e accessibile della derivata di e^-x. Ricordate, la matematica non è un ostacolo insormontabile, ma un insieme di strumenti potenti che ci permettono di comprendere e modellare il mondo che ci circonda.

La derivata di e^-x, pur essendo un concetto relativamente semplice, apre le porte a una vasta gamma di applicazioni pratiche. Padronizzare questo concetto vi permetterà di affrontare con sicurezza problemi in fisica, ingegneria, finanza e molti altri campi.

Ora che avete compreso la derivata di e^-x, quali altri concetti matematici vorreste esplorare? Quali applicazioni pratiche di questa derivata vi incuriosiscono di più? Vi invitiamo a continuare ad approfondire le vostre conoscenze matematiche e a scoprire le meraviglie che si celano dietro le equazioni e i numeri.