Criteri Di Congruenza Dei Triangoli Mappa Concettuale

Ti sei mai chiesto come fanno i geometri e gli architetti a costruire strutture precise e stabili? Una delle chiavi del loro successo risiede nella comprensione dei criteri di congruenza dei triangoli. Questi criteri, apparentemente semplici, sono fondamentali per dimostrare quando due triangoli sono esattamente uguali, ovvero congruenti. Questa guida, pensata per studenti di scuola media e superiore, ma utile anche per chiunque voglia rinfrescare le proprie conoscenze geometriche, ti accompagnerà attraverso i concetti chiave, presentandoli in modo chiaro e strutturato, con l'aiuto di una mappa concettuale ideale.

Cosa significa "congruenza" in geometria?

Prima di immergerci nei criteri specifici, è essenziale capire cosa significa congruenza. Due figure geometriche sono congruenti se, attraverso una serie di movimenti rigidi (traslazioni, rotazioni, riflessioni), una può essere sovrapposta perfettamente all'altra. In altre parole, hanno la stessa forma e le stesse dimensioni. Per i triangoli, la congruenza implica che tutti e tre i lati e tutti e tre gli angoli corrispondenti siano uguali.

I tre criteri di congruenza dei triangoli: Una panoramica

Esistono tre criteri fondamentali che ci permettono di dimostrare la congruenza di due triangoli senza dover misurare tutti i lati e gli angoli. Immagina questi criteri come delle "scorciatoie" che ci consentono di raggiungere la conclusione in modo efficiente.

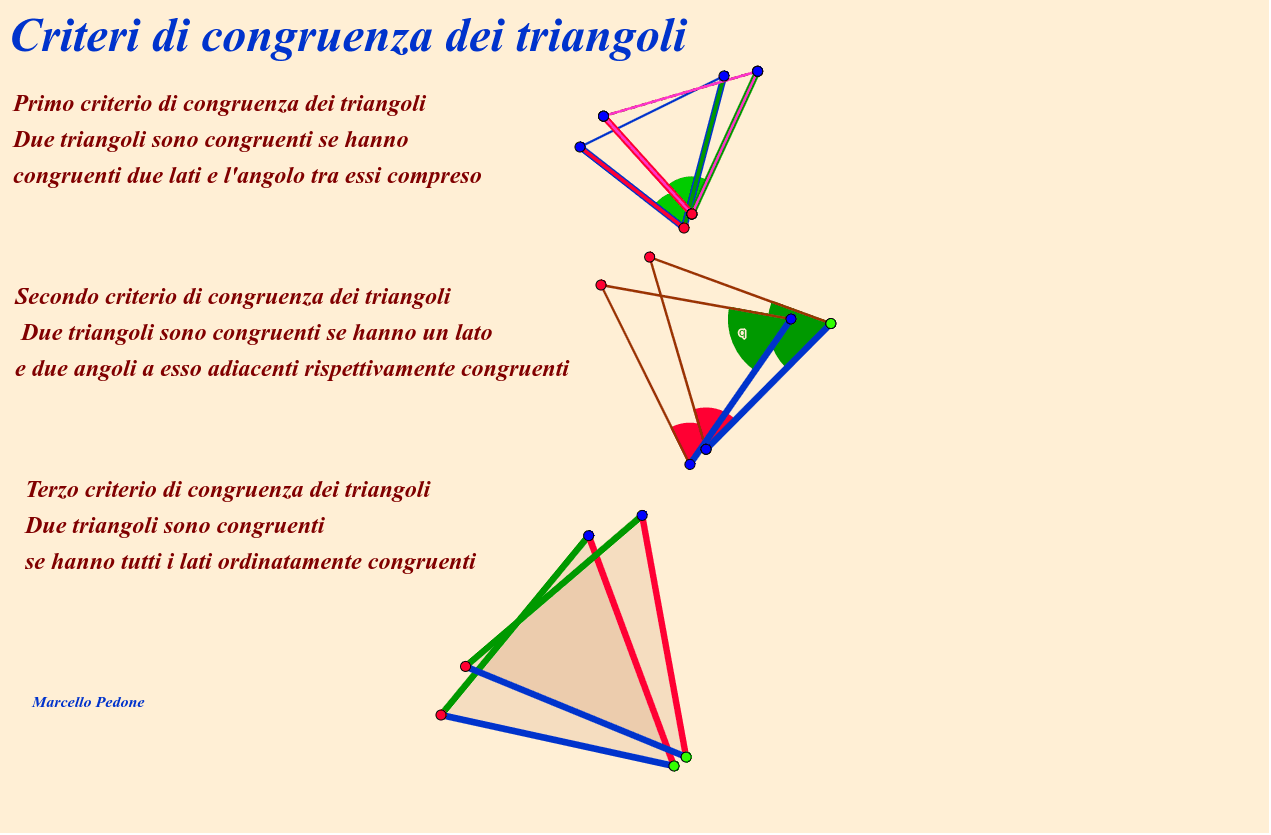
Primo criterio di congruenza (LAL): Lato-Angolo-Lato

Il primo criterio, spesso abbreviato come LAL (o SAS in inglese, Side-Angle-Side), afferma che se due triangoli hanno due lati congruenti e l'angolo compreso tra questi lati congruente, allora i due triangoli sono congruenti.

Spiegazione: Immagina di avere due lati di una certa lunghezza e l'angolo che li unisce. Questo "scheletro" definisce univocamente il triangolo. Non ci può essere un altro triangolo con quelle stesse caratteristiche che non sia esattamente uguale al primo.

Esempio: Considera due triangoli, ABC e DEF, tali che:

AB ≅ DE (il lato AB è congruente al lato DE)
AC ≅ DF (il lato AC è congruente al lato DF)
∠BAC ≅ ∠EDF (l'angolo BAC è congruente all'angolo EDF)

Secondo il primo criterio, il triangolo ABC è congruente al triangolo DEF (ΔABC ≅ ΔDEF).

Secondo criterio di congruenza (ALA): Angolo-Lato-Angolo

Il secondo criterio, abbreviato come ALA (o ASA in inglese, Angle-Side-Angle), stabilisce che se due triangoli hanno due angoli congruenti e il lato compreso tra questi angoli congruente, allora i due triangoli sono congruenti.

Spiegazione: In questo caso, abbiamo due angoli "fissati" e la distanza tra i loro vertici definita da un lato. Di nuovo, questo vincola la forma e le dimensioni del triangolo in modo univoco.

Esempio: Considera due triangoli, GHI e JKL, tali che:

∠GHI ≅ ∠JKL (l'angolo GHI è congruente all'angolo JKL)
∠GIH ≅ ∠JLK (l'angolo GIH è congruente all'angolo JLK)
GH ≅ JK (il lato GH è congruente al lato JK)

Secondo il secondo criterio, il triangolo GHI è congruente al triangolo JKL (ΔGHI ≅ ΔJKL).

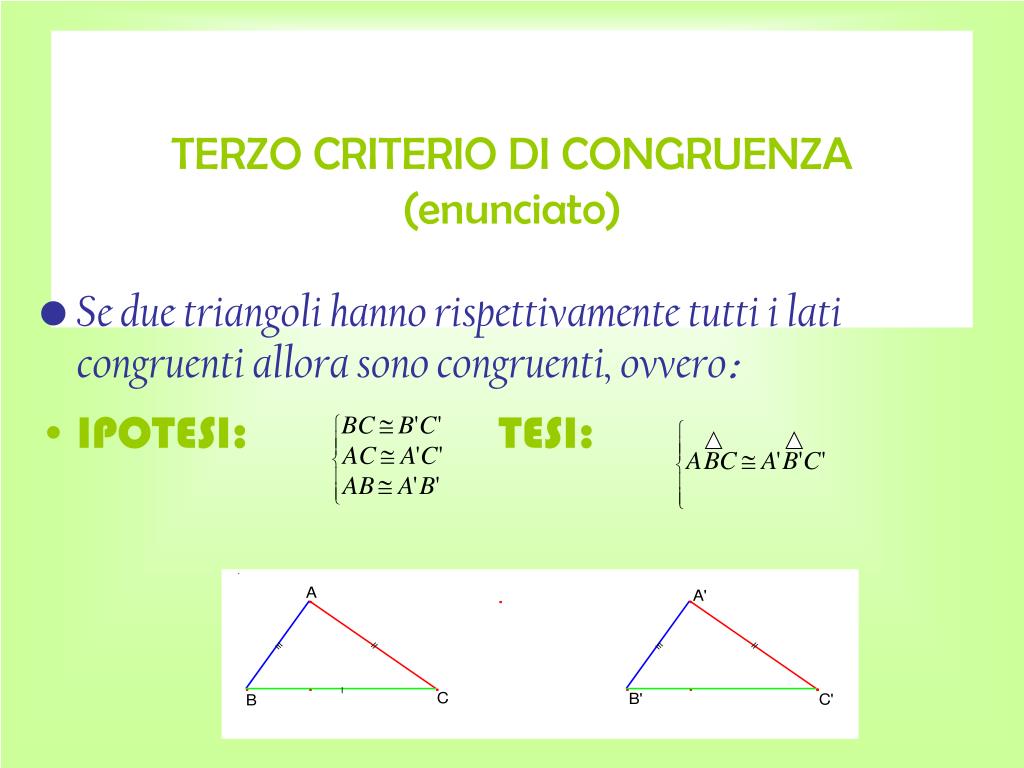
Terzo criterio di congruenza (LLL): Lato-Lato-Lato

Il terzo criterio, abbreviato come LLL (o SSS in inglese, Side-Side-Side), afferma che se due triangoli hanno tutti e tre i lati congruenti, allora i due triangoli sono congruenti.

Spiegazione: Se conosciamo la lunghezza di tutti e tre i lati di un triangolo, non c'è modo di costruire un triangolo diverso (a meno di rotazioni o riflessioni). La forma e le dimensioni sono completamente determinate.

Esempio: Considera due triangoli, MNO e PQR, tali che:

MN ≅ PQ (il lato MN è congruente al lato PQ)
NO ≅ QR (il lato NO è congruente al lato QR)
OM ≅ RP (il lato OM è congruente al lato RP)

Secondo il terzo criterio, il triangolo MNO è congruente al triangolo PQR (ΔMNO ≅ ΔPQR).

Come utilizzare i criteri di congruenza: un approccio pratico

Ora che conosciamo i criteri, vediamo come applicarli nella pratica. La chiave è identificare le informazioni che abbiamo sui due triangoli che stiamo analizzando e poi cercare di farle corrispondere a uno dei criteri.

Leggi attentamente il problema: Identifica cosa ti viene dato come informazione (lati, angoli, ecc.).
Disegna un diagramma: Un disegno preciso ti aiuterà a visualizzare i triangoli e le loro parti.
Cerca corrispondenze: Confronta le informazioni che hai con i criteri LAL, ALA e LLL.
Scrivi la dimostrazione: Una volta identificato il criterio applicabile, scrivi una dimostrazione formale che mostri come le informazioni date soddisfano le condizioni del criterio.
Conclusione: Concludi affermando che i due triangoli sono congruenti in base al criterio utilizzato.

Mappa Concettuale (Ideale) per i Criteri di Congruenza dei Triangoli

Una mappa concettuale può aiutarti a visualizzare la relazione tra i diversi concetti. Immagina una mappa con al centro l'argomento principale: "Criteri di Congruenza dei Triangoli". Da questo punto centrale, si diramano tre rami principali, uno per ciascun criterio (LAL, ALA, LLL). Ogni ramo include:

Il nome del criterio (es. Primo criterio di congruenza)
L'abbreviazione (es. LAL)
Una breve descrizione (es. Due lati e l'angolo compreso congruenti)
Un esempio (disegno semplificato dei triangoli con le parti congruenti indicate)

Questa mappa visuale ti permette di avere una panoramica chiara e immediata dei criteri e delle loro caratteristiche principali.

Importanza dei criteri di congruenza

I criteri di congruenza non sono solo un esercizio teorico. Hanno importanti applicazioni pratiche in diversi campi:

Architettura e Ingegneria: Per garantire la stabilità e la precisione delle costruzioni.
Topografia: Per misurare distanze e angoli con precisione.
Grafica Computerizzata: Per creare modelli 3D e animazioni.
Risoluzione di problemi geometrici: Sono strumenti essenziali per dimostrare teoremi e risolvere problemi più complessi.

Consigli aggiuntivi per lo studio

Ecco alcuni consigli per affrontare al meglio lo studio dei criteri di congruenza:

Esercitati, esercitati, esercitati! La pratica è fondamentale per acquisire familiarità con i criteri e imparare a identificarli nei problemi.
Chiarisci i dubbi: Se hai difficoltà, non esitare a chiedere aiuto al tuo insegnante o a cercare spiegazioni online.
Utilizza risorse online: Esistono numerosi siti web e video che offrono spiegazioni, esempi e esercizi sui criteri di congruenza.
Collabora con i tuoi compagni: Studiare insieme può aiutarti a comprendere meglio i concetti e a risolvere i problemi in modo più efficace.
Non memorizzare meccanicamente: Cerca di capire il *perché* i criteri funzionano, non solo di memorizzarli. Questo ti aiuterà a ricordarli più facilmente e ad applicarli in modo corretto.

Oltre i criteri di congruenza: la similitudine

È importante distinguere la congruenza dalla similitudine. Due figure sono simili se hanno la stessa forma, ma dimensioni diverse. I triangoli simili hanno gli angoli corrispondenti congruenti e i lati corrispondenti proporzionali. Esistono anche criteri di similitudine, ma questo è un argomento a parte!

Conclusione

I criteri di congruenza dei triangoli sono uno strumento potente e versatile per la risoluzione di problemi geometrici e per la comprensione del mondo che ci circonda. Comprendere e padroneggiare questi criteri ti aprirà le porte a concetti più avanzati e ti fornirà le basi per affrontare sfide più complesse in matematica e nelle discipline scientifiche. Ricorda: la pratica costante e la comprensione dei concetti sono le chiavi del successo! Approfondisci, esercitati e non aver paura di sperimentare. La geometria, come la vita, è un viaggio di scoperta.