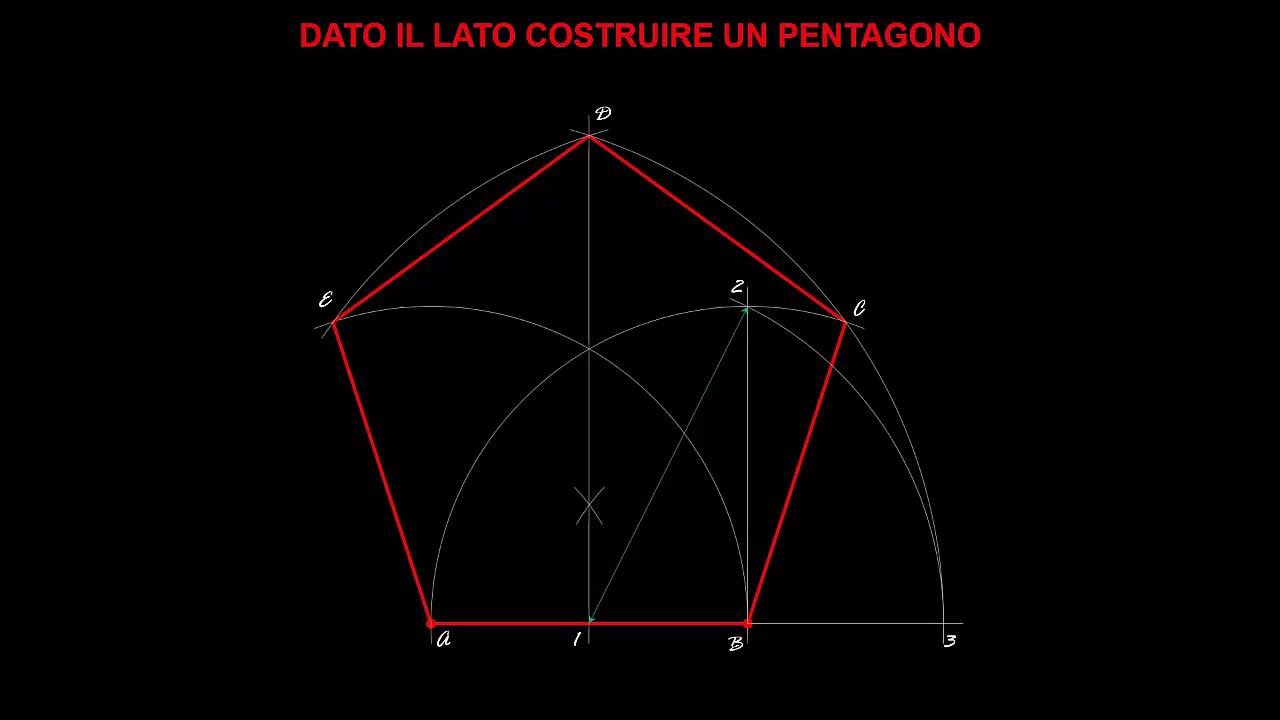
Costruzione Di Un Pentagono Dato Il Raggio

La costruzione geometrica di un pentagono regolare dato il raggio del cerchio circoscritto è un problema classico che affascina matematici e appassionati da secoli. Diversamente dalla costruzione con un compasso e un righello di un pentagono dato il lato, questa variante presenta sfide uniche. Esploreremo qui i metodi per realizzare questa costruzione, concentrandoci sulla precisione e sui principi matematici sottostanti.
Fondamenti Teorici e Geometrici
Prima di procedere alla costruzione pratica, è essenziale comprendere i fondamenti teorici che la supportano. Un pentagono regolare ha cinque lati uguali e cinque angoli interni uguali. Ciascun angolo interno misura 108 gradi. La chiave per costruire un pentagono regolare inscritto in un cerchio è dividere il cerchio in cinque archi uguali, e questo equivale a dividere l'angolo completo di 360 gradi in cinque parti uguali, ciascuna di 72 gradi.
Il Ruolo del Numero Aureo
Il numero aureo (φ ≈ 1.618) gioca un ruolo cruciale nella geometria del pentagono. La diagonale di un pentagono regolare è φ volte la lunghezza del suo lato. Questa proporzione divina è intrinsecamente legata alle relazioni tra gli elementi del pentagono e alla possibilità di costruirlo geometricamente. Molti metodi di costruzione si basano proprio su questa relazione proporzionale.
Analisi Trigonometrica
L'approccio trigonometrico fornisce un'altra prospettiva. Se r è il raggio del cerchio circoscritto, la lunghezza del lato s del pentagono può essere calcolata come: s = 2r * sin(π/5) = 2r * sin(36°) Questa formula deriva dall'analisi del triangolo isoscele formato dal centro del cerchio e due vertici adiacenti del pentagono.
Metodi di Costruzione Pratici
Esistono diversi metodi per costruire un pentagono dato il raggio, alcuni più complessi di altri. Presenteremo un metodo relativamente semplice e preciso che utilizza compasso e righello.
Metodo di Richmond
Il metodo di Richmond è un approccio elegante e relativamente accessibile:
- Disegna un cerchio con centro O e raggio r.
- Traccia un diametro orizzontale AB.
- Traccia un diametro verticale CD, perpendicolare ad AB.
- Trova il punto medio E del segmento OB.
- Con un compasso puntato in E, apri fino a C e traccia un arco che interseca AB in F.
- La lunghezza CF è la lunghezza del lato del pentagono.
- Con un compasso puntato in C, apri con raggio CF e segna un punto G sul cerchio.
- Ripeti il processo partendo da G per trovare altri punti sul cerchio, distanziati della stessa distanza CF.
- Collega i cinque punti sul cerchio per formare il pentagono.
Altre Variazioni e Considerazioni
Esistono delle variazioni di questo metodo, e alcune possono essere più adatte a certe situazioni pratiche. La precisione della costruzione dipende dalla cura con cui si eseguono i passaggi. L'uso di un compasso ben affilato e di un righello preciso è fondamentale. L'errore di costruzione può accumularsi, quindi è bene controllare la chiusura del pentagono alla fine.
Importanza e Applicazioni
La costruzione del pentagono non è solo un esercizio teorico. Ha importanti applicazioni pratiche in vari campi:
Architettura e Design
Il pentagono e le sue derivazioni geometriche sono elementi ricorrenti nell'architettura e nel design. Dalle piante di edifici a forme decorative, la proporzione armonica del pentagono lo rende esteticamente piacevole e funzionale. Il Pentagono di Washington D.C., l'edificio che ospita il Dipartimento della Difesa degli Stati Uniti, è un esempio iconico di come la forma pentagonale possa essere utilizzata per ottimizzare lo spazio e la funzionalità.
Cristallografia
In cristallografia, lo studio delle strutture cristalline, il pentagono è meno comune rispetto a forme come cubi e esagoni a causa della sua incapacità di tassellare lo spazio tridimensionale in modo regolare. Tuttavia, si trova in alcune strutture quasicristalline, che mostrano un ordine a lungo raggio ma non sono periodiche come i cristalli tradizionali. I quasicristalli con simmetria icosaedrica, per esempio, presentano elementi pentagonali.
Arte e Simbolismo
Il pentagono ha un significato simbolico in molte culture. La stella a cinque punte, o pentagramma, derivata dal pentagono, è stata usata come simbolo di protezione, conoscenza e perfezione in diverse tradizioni. La sua presenza nell'arte e nel simbolismo testimonia il suo fascino duraturo.
Limitazioni e Sfide
La costruzione precisa di un pentagono dato il raggio, utilizzando solo compasso e righello, presenta delle limitazioni. Anche con i metodi più accurati, è difficile ottenere una precisione assoluta. L'accumulo di errori nei vari passaggi può portare a piccole imperfezioni nella forma finale. Inoltre, alcuni metodi sono più sensibili agli errori di altri.
Errori di Approssimazione
La precisione della costruzione dipende dalla capacità di tracciare archi e linee con precisione e di individuare i punti di intersezione con esattezza. Anche piccole imprecisioni in questi passaggi possono portare a errori di approssimazione. Utilizzare strumenti di alta qualità e lavorare con cura può minimizzare questi errori.
Alternative con Software di Geometria
Con l'avvento del software di geometria dinamica (come GeoGebra), la costruzione di pentagoni è diventata molto più semplice e precisa. Questi strumenti permettono di definire il raggio del cerchio e di costruire il pentagono con un alto grado di precisione utilizzando comandi specifici. Offrono anche la possibilità di visualizzare e analizzare le relazioni geometriche in modo interattivo.
Conclusioni e Prospettive Future
La costruzione di un pentagono dato il raggio è un esercizio che combina abilità geometriche, precisione e comprensione dei principi matematici. Mentre i metodi tradizionali con compasso e righello offrono un'esperienza tangibile e stimolante, il software di geometria fornisce alternative più precise ed efficienti. Comprendere i fondamenti teorici e le limitazioni pratiche di ciascun approccio è essenziale per apprezzare la bellezza e la complessità di questa sfida geometrica.
Invitiamo il lettore a sperimentare i diversi metodi di costruzione e a confrontare i risultati. Che si utilizzi compasso e righello, o software specializzato, l'esplorazione della geometria del pentagono è un'attività gratificante che stimola la creatività e la comprensione delle relazioni matematiche.
Continua ad esplorare il mondo della geometria!