Coseno E Seno Di Un Angolo

Quante volte ci siamo imbattuti in concetti matematici come il coseno e il seno di un angolo, magari a scuola o in contesti più specifici, sentendoci un po' spaesati? Forse li abbiamo memorizzati per superare un esame, senza però comprenderne a fondo il significato e l'importanza. La verità è che il coseno e il seno, pilastri della trigonometria, sono fondamentali per comprendere e descrivere il mondo che ci circonda, ben al di là delle noiose equazioni.

Questo articolo si propone di demistificare questi concetti, rendendoli accessibili a tutti, anche a chi si sente un po' arrugginito con la matematica. Cercheremo di capire perché sono così importanti, come vengono utilizzati in pratica e, soprattutto, come possono aiutarci a vedere il mondo con occhi diversi.

Coseno e Seno: Cosa Sono?

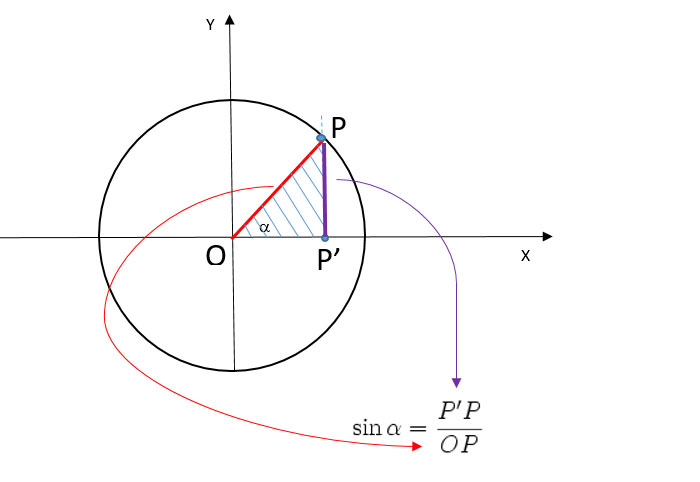
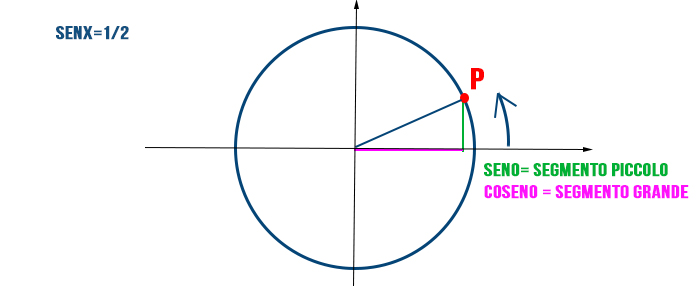
Partiamo dalle basi. Immaginiamo un cerchio centrato nell'origine di un sistema di assi cartesiani (x, y). Questo cerchio ha un raggio unitario, ovvero di lunghezza 1. Ora, prendiamo un punto qualsiasi su questo cerchio e tracciamo una retta che lo collega all'origine. L'angolo che questa retta forma con l'asse x positivo è l'angolo di cui stiamo parlando.

Il coseno di questo angolo è semplicemente la coordinata x del punto sul cerchio. In altre parole, è la distanza orizzontale del punto dall'asse y.
Il seno dell'angolo, invece, è la coordinata y del punto, ovvero la distanza verticale del punto dall'asse x.

Per visualizzare meglio, pensa a un raggio di bicicletta che ruota attorno al mozzo. L'angolo che il raggio forma con l'orizzontale cambia continuamente, e di conseguenza cambiano anche le coordinate del punto sulla circonferenza descritta dal raggio. Il coseno e il seno descrivono proprio queste variazioni.

Perché un Cerchio di Raggio Unitario?

L'uso di un cerchio di raggio unitario semplifica enormemente i calcoli. Se il raggio fosse diverso da 1, dovremmo dividere le coordinate x e y per il valore del raggio per ottenere il coseno e il seno. Il cerchio unitario ci permette di leggere direttamente il coseno e il seno come coordinate del punto sulla circonferenza.

È importante sottolineare che il coseno e il seno sono funzioni periodiche. Questo significa che si ripetono dopo un certo intervallo, precisamente ogni 360 gradi (o 2π radianti). Immagina di far fare un giro completo al punto sul cerchio. Dopo 360 gradi, ritorna alla posizione di partenza e i valori di coseno e seno si ripetono.

Applicazioni Pratiche del Coseno e del Seno

Ok, abbiamo capito la definizione, ma a cosa servono realmente coseno e seno al di fuori dei libri di testo? La risposta è: a moltissime cose! Eccone alcuni esempi:

Navigazione: I sistemi di navigazione GPS utilizzano la trigonometria, e quindi il coseno e il seno, per calcolare la posizione di un oggetto sulla Terra. Considera che la Terra è approssimativamente sferica, e le coordinate geografiche (latitudine e longitudine) sono espresse in termini di angoli.
Fisica: In fisica, il coseno e il seno sono fondamentali per descrivere moti oscillatori (come il moto di un pendolo) e onde (come le onde sonore o luminose). Ad esempio, la proiezione dell'ombra di un oggetto che si muove di moto circolare uniforme descrive un moto armonico semplice, che è modellato proprio con funzioni trigonometriche.
Ingegneria: Gli ingegneri utilizzano il coseno e il seno per calcolare le forze agenti su una struttura, come un ponte o un edificio. Quando una forza agisce su un angolo rispetto a una superficie, viene scomposta nelle sue componenti orizzontali e verticali, utilizzando proprio il coseno e il seno dell'angolo.
Grafica Computerizzata: Nel mondo della grafica computerizzata, il coseno e il seno sono usati per ruotare, scalare e deformare oggetti 3D. Pensa ai videogiochi o ai film di animazione: dietro la fluidità dei movimenti dei personaggi c'è un calcolo trigonometrico continuo.
Musica: Il suono è un'onda, e le onde sono descritte da funzioni sinusoidali (che utilizzano seno e coseno). L'altezza di una nota musicale è direttamente correlata alla frequenza dell'onda sonora, e la frequenza è un parametro fondamentale nelle funzioni trigonometriche.

Questi sono solo alcuni esempi, ma la verità è che il coseno e il seno sono presenti in moltissimi altri ambiti, spesso senza che ce ne rendiamo conto. Dalla progettazione di antenne paraboliche alla costruzione di strumenti musicali, la trigonometria gioca un ruolo cruciale.

Controparti e Sfide

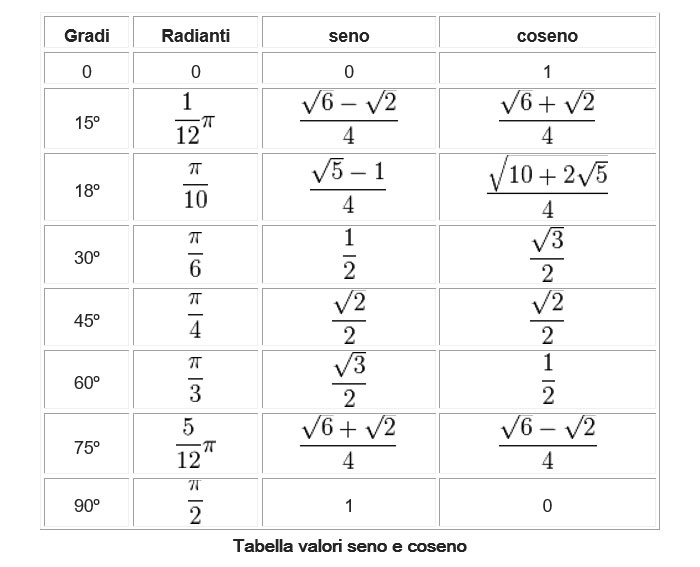
Nonostante la loro importanza, il coseno e il seno possono presentare delle sfide per chi si avvicina a questi concetti per la prima volta. Alcuni potrebbero obiettare che sono troppo astratti e difficili da visualizzare, soprattutto se non si ha una solida base di geometria. Altri potrebbero lamentare la necessità di memorizzare tabelle di valori specifici per alcuni angoli notevoli.

È vero, la memorizzazione di tabelle può sembrare un'attività noiosa e priva di significato. Tuttavia, con la pratica e la comprensione delle relazioni tra gli angoli, i valori diventano più intuitivi. Inoltre, oggi abbiamo a disposizione calcolatrici e software che ci permettono di calcolare il coseno e il seno di qualsiasi angolo in modo rapido e preciso.

Un'altra sfida è la comprensione del radiante, l'unità di misura degli angoli utilizzata in matematica e fisica. Il radiante può sembrare un concetto strano all'inizio, ma in realtà è più naturale del grado. Un radiante è definito come l'angolo sotteso da un arco di circonferenza di lunghezza pari al raggio. Questo legame diretto tra l'angolo e la lunghezza dell'arco semplifica molti calcoli e rende le formule più eleganti.

Un Approccio Soluzione-Focalizzato

Come possiamo superare queste sfide e rendere il coseno e il seno più accessibili e comprensibili? Ecco alcune idee:

Visualizzazione: Utilizzare software di geometria dinamica o applet interattive per visualizzare il cerchio unitario e le variazioni del coseno e del seno al variare dell'angolo. L'interattività aiuta a creare una connessione più forte tra il concetto astratto e la rappresentazione visiva.
Esempi concreti: Concentrarsi su esempi pratici e reali che dimostrino l'utilità del coseno e del seno. Collegare la teoria alla pratica rende l'apprendimento più motivante e significativo.
Analogia: Utilizzare analogie e metafore per spiegare i concetti in modo più intuitivo. Ad esempio, paragonare il coseno e il seno alle componenti di una forza che agisce su un oggetto.
Pratica: Risolvere esercizi e problemi che richiedano l'uso del coseno e del seno in diversi contesti. La pratica costante rafforza la comprensione e sviluppa la capacità di applicare i concetti in modo flessibile.
Risorse online: Sfruttare le numerose risorse online disponibili, come tutorial, video e forum di discussione. Internet offre un'ampia gamma di strumenti per l'apprendimento autonomo e la risoluzione di dubbi.

Ricorda: la matematica, come ogni altra disciplina, richiede tempo e impegno. Non scoraggiarti di fronte alle difficoltà, ma persevera e cerca di affrontare i concetti con curiosità e apertura mentale. La soddisfazione di comprendere un concetto matematico e di vederne le applicazioni nel mondo reale è impagabile.

Oltre i Numeri: Una Nuova Prospettiva

Il coseno e il seno non sono solo numeri o funzioni matematiche. Sono strumenti potenti che ci permettono di descrivere e comprendere il mondo che ci circonda. Ci aiutano a navigare, a costruire ponti, a creare immagini digitali e a comporre musica. Ci offrono una nuova prospettiva sulla realtà, rivelando la matematica nascosta dietro i fenomeni naturali e le creazioni umane.

La prossima volta che ti imbatterai in un'onda, in un edificio o in un suono, fermati un attimo a pensare al coseno e al seno. Prova a immaginare come questi concetti matematici contribuiscono a modellare e a spiegare ciò che stai osservando. Potresti scoprire un mondo nuovo e affascinante.

E ora, ti invito a riflettere: in quale altro ambito della tua vita quotidiana pensi che il coseno e il seno possano giocare un ruolo, anche se nascosto? Prova a fare qualche ricerca o a chiedere a un esperto. Potresti rimanere sorpreso dalle scoperte che farai.