Cos'è Il Seno Di Un Angolo

Il seno di un angolo è una delle funzioni trigonometriche fondamentali, con un ruolo cruciale in matematica, fisica, ingegneria e in molti altri campi scientifici. Comprendere a fondo cos'è il seno di un angolo e come viene calcolato è essenziale per risolvere problemi complessi e interpretare fenomeni del mondo reale.
Definizione Formale
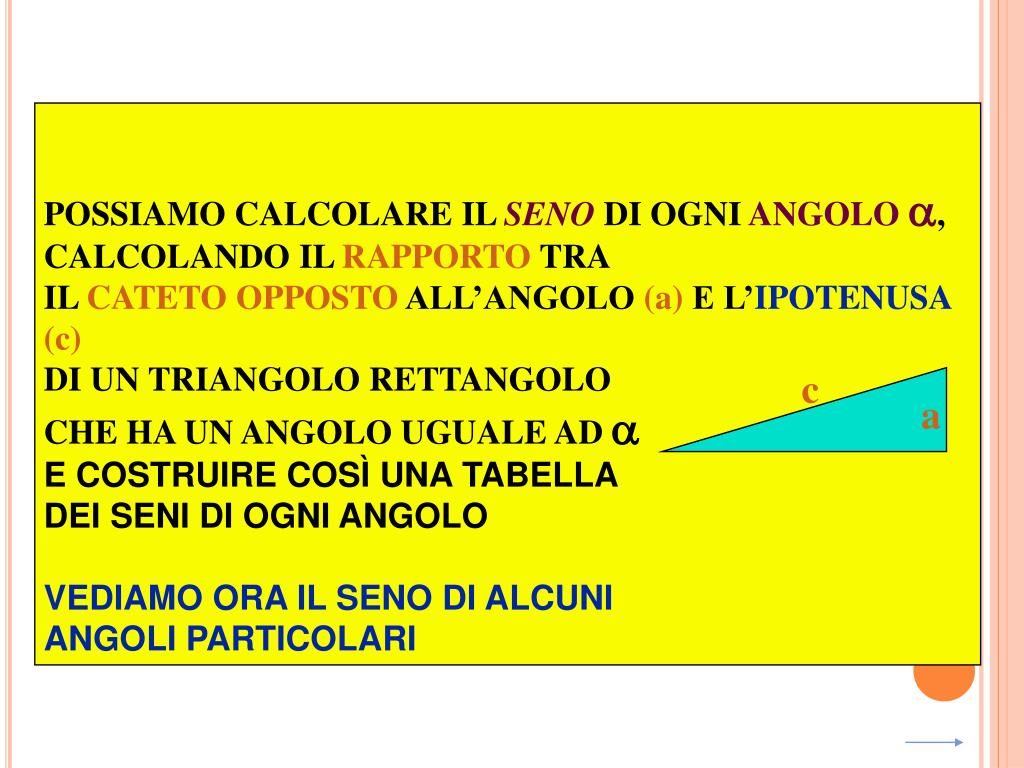
Formalmente, il seno di un angolo (spesso abbreviato come sin θ) in un triangolo rettangolo è definito come il rapporto tra la lunghezza del cateto opposto all'angolo e la lunghezza dell'ipotenusa. In termini più semplici:
sin θ = (lunghezza del cateto opposto) / (lunghezza dell'ipotenusa)
Dove:
- θ (theta) rappresenta l'angolo che stiamo considerando.
- Il cateto opposto è il lato del triangolo rettangolo che si trova di fronte all'angolo θ.
- L'ipotenusa è il lato più lungo del triangolo rettangolo, opposto all'angolo retto (90 gradi).
Estensione al Cerchio Trigonometrico
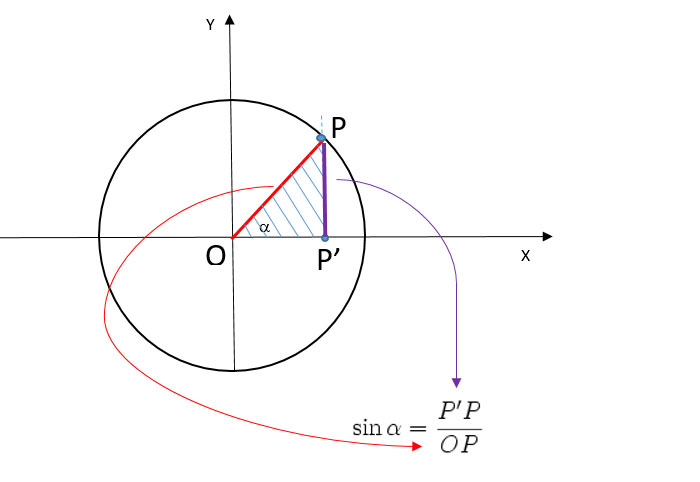
La definizione basata sul triangolo rettangolo è valida solo per angoli compresi tra 0 e 90 gradi (0 e π/2 radianti). Per estendere la definizione a tutti gli angoli, si utilizza il cerchio trigonometrico (o cerchio unitario). Il cerchio trigonometrico è un cerchio con raggio 1 centrato nell'origine di un sistema di coordinate cartesiane.
Dato un angolo θ misurato in senso antiorario a partire dall'asse x positivo, il seno di θ è definito come la coordinata y del punto in cui il raggio che forma l'angolo θ interseca il cerchio trigonometrico.
Questa definizione del cerchio trigonometrico permette di definire il seno per qualsiasi angolo, anche negativo o superiore a 360 gradi (2π radianti). Il seno varia tra -1 e 1.
Proprietà e Caratteristiche del Seno
La funzione seno possiede diverse proprietà importanti:
Periodicità
La funzione seno è periodica con un periodo di 2π radianti (360 gradi). Questo significa che sin(θ + 2π) = sin(θ) per ogni angolo θ. In altre parole, il valore del seno si ripete ogni 360 gradi.
Simmetria
La funzione seno è una funzione dispari. Questo significa che sin(-θ) = -sin(θ). Geometricamente, questo implica che il grafico del seno è simmetrico rispetto all'origine.
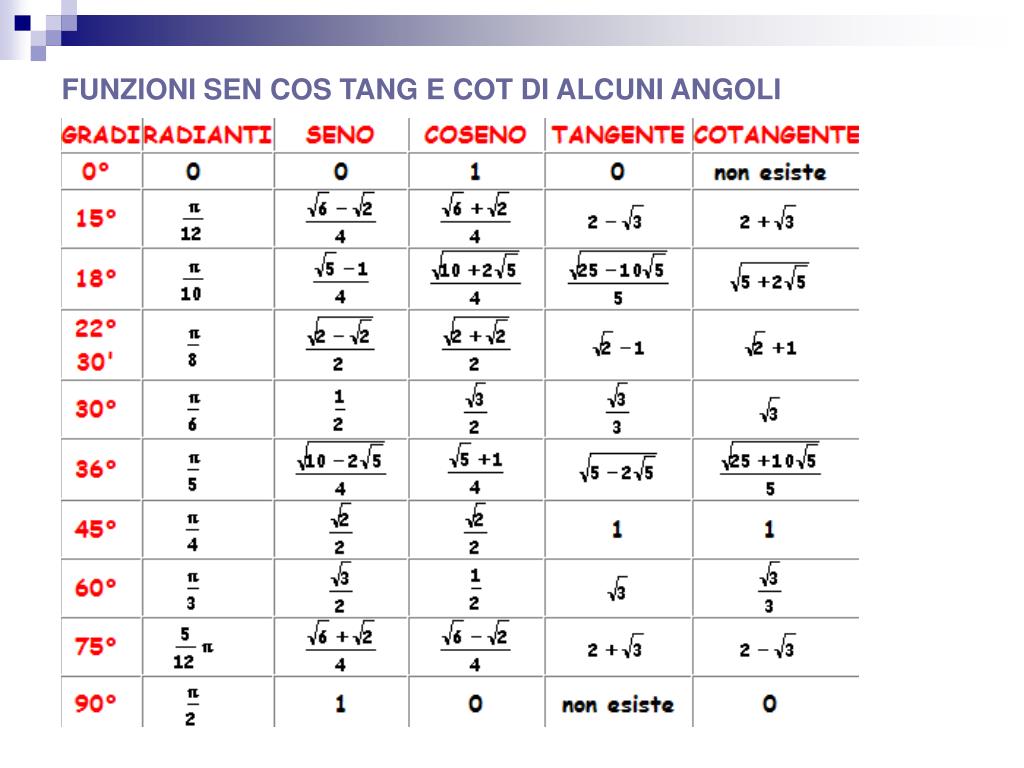
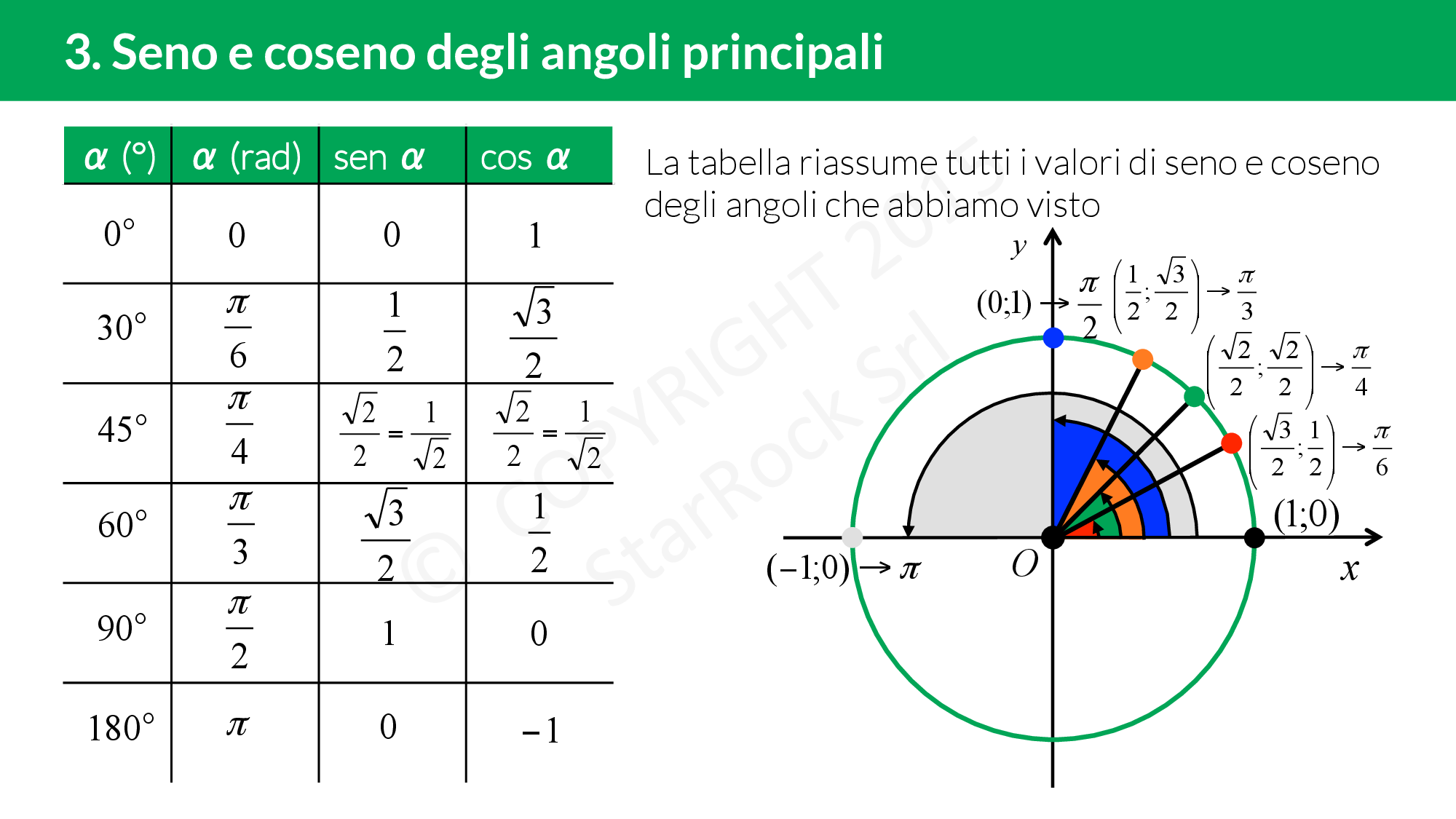
Valori Notevoli
Alcuni valori del seno sono particolarmente importanti e vengono usati frequentemente:
- sin(0°) = sin(0) = 0
- sin(30°) = sin(π/6) = 1/2
- sin(45°) = sin(π/4) = √2/2
- sin(60°) = sin(π/3) = √3/2
- sin(90°) = sin(π/2) = 1
- sin(180°) = sin(π) = 0
- sin(270°) = sin(3π/2) = -1
- sin(360°) = sin(2π) = 0
Grafico
Il grafico della funzione seno è un'onda sinusoidale che oscilla tra -1 e 1. L'asse x rappresenta l'angolo (in radianti o gradi), mentre l'asse y rappresenta il valore del seno di quell'angolo. Il grafico mostra chiaramente la periodicità e la simmetria della funzione.
Come Calcolare il Seno
Ci sono diversi modi per calcolare il seno di un angolo:
Utilizzo di una Calcolatrice
Il modo più semplice è utilizzare una calcolatrice scientifica. Assicurarsi che la calcolatrice sia impostata sulla modalità corretta (gradi o radianti) prima di inserire l'angolo.
Tavole Trigonometriche
In passato, si utilizzavano le tavole trigonometriche, che elencavano i valori del seno per diversi angoli. Anche se meno comuni oggi, possono essere utili in contesti in cui non è disponibile una calcolatrice.
Serie di Taylor
Per un calcolo più preciso, si può utilizzare la serie di Taylor per approssimare il seno di un angolo:
sin(x) = x - x³/3! + x⁵/5! - x⁷/7! + ...
Dove x è l'angolo in radianti e n! rappresenta il fattoriale di n. Più termini si includono nella serie, più precisa sarà l'approssimazione.
Relazioni Trigonometriche
Il seno può anche essere calcolato utilizzando altre relazioni trigonometriche, come l'identità fondamentale:
sin²(θ) + cos²(θ) = 1
Se si conosce il coseno dell'angolo, si può calcolare il seno come:
sin(θ) = ±√(1 - cos²(θ))
È importante determinare il segno corretto in base al quadrante in cui si trova l'angolo.
Applicazioni Reali
Il seno di un angolo ha innumerevoli applicazioni nel mondo reale:
Fisica
In fisica, il seno è utilizzato per calcolare le componenti di un vettore, ad esempio la componente verticale della velocità di un proiettile. È anche fondamentale nello studio delle onde, come le onde sonore e le onde luminose. L'ampiezza di un'onda sinusoidale, che descrive molte onde fisiche, è direttamente legata al valore del seno.
Ingegneria
In ingegneria, il seno è utilizzato per calcolare le forze agenti su una struttura, come un ponte o un edificio. È anche cruciale nella progettazione di circuiti elettrici e nella navigazione. Ad esempio, il calcolo degli angoli di elevazione per le antenne paraboliche si basa sull'uso del seno e del coseno.
Navigazione
Nella navigazione, il seno è utilizzato per determinare la posizione di una nave o di un aereo. I sistemi GPS utilizzano triangolazioni complesse che si basano su calcoli trigonometrici, inclusi quelli del seno, per determinare la posizione esatta.
Grafica Computerizzata
Nella grafica computerizzata, il seno è utilizzato per creare animazioni, modellare superfici e generare effetti speciali. Le funzioni sinusoidali sono ampiamente utilizzate per simulare movimenti ondulatori e oscillazioni.
Musica
In musica, le onde sonore possono essere descritte utilizzando funzioni sinusoidali. L'altezza di un suono è correlata alla frequenza dell'onda, mentre l'ampiezza è legata all'intensità (volume). L'analisi spettrale del suono si basa sulla decomposizione del segnale in componenti sinusoidali.
Esempio Concreto: Altezza di un Albero
Immagina di voler calcolare l'altezza di un albero. Ti trovi a una certa distanza dall'albero e misuri l'angolo di elevazione (l'angolo tra la linea di vista e l'orizzontale) verso la cima dell'albero. Conoscendo la distanza dall'albero (il cateto adiacente) e l'angolo di elevazione, puoi utilizzare la tangente dell'angolo per calcolare l'altezza dell'albero (il cateto opposto). Tuttavia, se hai misurato l'ipotenusa (la distanza in linea retta dalla tua posizione alla cima dell'albero), puoi usare il seno dell'angolo di elevazione per calcolare l'altezza:
Altezza dell'albero = Ipotenusa * sin(angolo di elevazione)
Conclusione
Il seno di un angolo è un concetto fondamentale della trigonometria con applicazioni pervasive in molte discipline scientifiche e ingegneristiche. La sua definizione, le sue proprietà e le sue applicazioni lo rendono uno strumento essenziale per la comprensione e la modellazione del mondo che ci circonda.
Per approfondire la tua comprensione, ti incoraggio a esplorare ulteriori risorse online, a esercitarti con problemi pratici e a sperimentare con software di matematica. Comprendere il seno è un passo importante verso una più profonda comprensione della matematica e delle sue applicazioni.