Cosa Sono I Limiti In Matematica

Ti sei mai chiesto cosa succede quando ti avvicini a un bordo, a un confine? Immagina di camminare verso il precipizio di una montagna. Più ti avvicini, più la vista diventa spettacolare, ma non puoi superare il bordo senza conseguenze. In matematica, il concetto di limite cattura proprio questa idea di avvicinarsi a un valore, senza necessariamente raggiungerlo. Molti studenti trovano i limiti ostici, un po' come un puzzle difficile da risolvere. Ma non temere! Cercheremo di rendere questo argomento più chiaro e accessibile.

I limiti sono fondamentali in moltissimi rami della matematica, dal calcolo infinitesimale all'analisi numerica. Capire cosa sono è cruciale per affrontare argomenti più avanzati.

Cosa Sono Esattamente i Limiti?

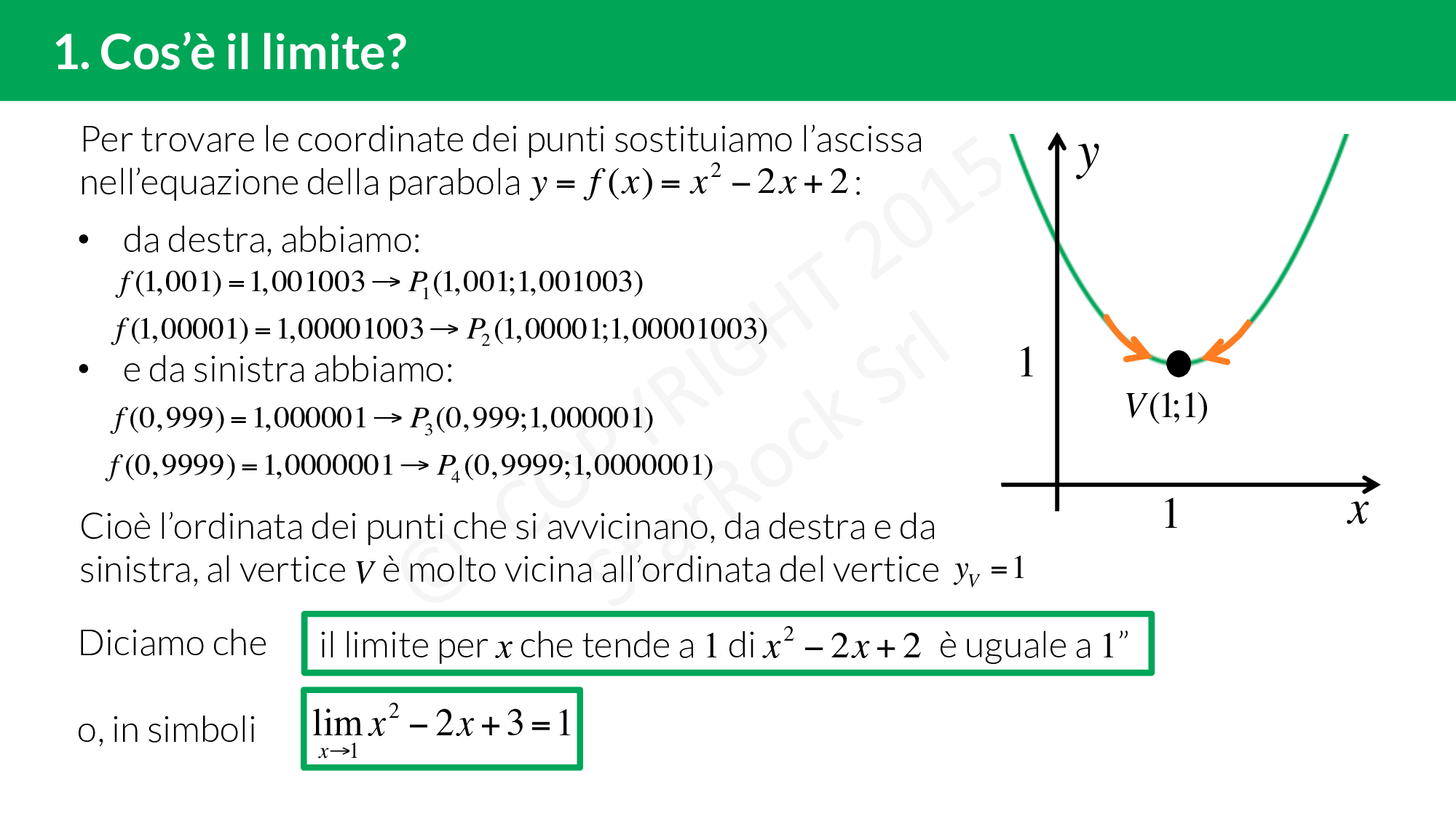
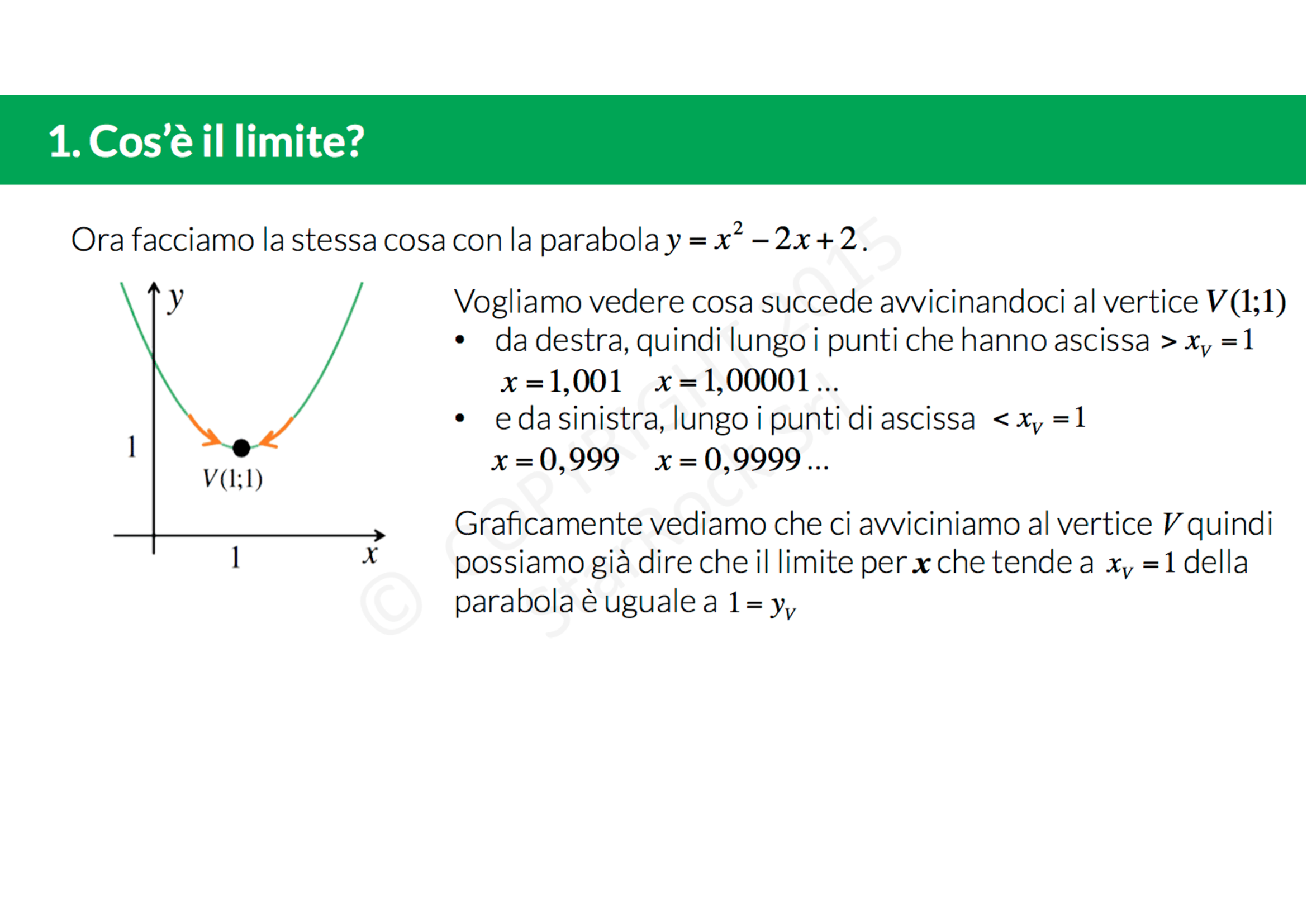
In termini semplici, un limite descrive il comportamento di una funzione quando l'input (la variabile indipendente) si avvicina a un certo valore. Non ci interessa cosa succede *esattamente* a quel valore, ma piuttosto cosa succede *nelle sue vicinanze*. È come osservare una persona che si avvicina a una porta: ci interessa capire dove sta andando, non necessariamente cosa farà una volta oltrepassata la soglia.

Formalmente, possiamo dire che il limite di una funzione f(x) quando x tende a un valore "c" è uguale a "L" se, avvicinandoci a "c", i valori di f(x) si avvicinano sempre di più a "L". Si scrive:

lim_x→c f(x) = L

Questa notazione, apparentemente complessa, significa semplicemente: "Il limite di f(x) quando x tende a c è uguale a L."

Esempio pratico: Immagina la funzione f(x) = (x² - 1) / (x - 1). Se provi a sostituire x = 1, ottieni una divisione per zero, che è indefinita. Tuttavia, possiamo semplificare la funzione come f(x) = x + 1 (per x ≠ 1). Ora, se x si avvicina a 1, f(x) si avvicina a 2. Quindi, lim_x→1 (x² - 1) / (x - 1) = 2.

Perché Sono Importanti i Limiti?

I limiti sono il fondamento del calcolo infinitesimale. Senza di essi, non potremmo definire concetti cruciali come:

* Derivate: La derivata di una funzione in un punto rappresenta la pendenza della retta tangente alla funzione in quel punto. Questa pendenza è definita proprio come un limite. * Integrali: L'integrale di una funzione rappresenta l'area sotto la curva. Anche in questo caso, l'integrale è definito come il limite di una somma. * Continuità: Una funzione è continua in un punto se il limite della funzione in quel punto è uguale al valore della funzione in quel punto.

Inoltre, i limiti trovano applicazioni in molti altri campi, come:

* Fisica: Calcolo della velocità e dell'accelerazione istantanee. * Economia: Analisi dei mercati e delle tendenze economiche. * Ingegneria: Progettazione di strutture e sistemi complessi.

Come Calcolare i Limiti

Esistono diverse tecniche per calcolare i limiti. Alcune delle più comuni sono:

* Sostituzione diretta: Se la funzione è continua nel punto in cui stiamo calcolando il limite, possiamo semplicemente sostituire il valore di x nella funzione. * Semplificazione algebrica: A volte, possiamo semplificare l'espressione della funzione per eliminare le indeterminate (come la divisione per zero). * Razionalizzazione: Se la funzione contiene radici, possiamo razionalizzare il numeratore o il denominatore per semplificare l'espressione. * Teorema del confronto (Sandwich Theorem): Se una funzione è "compressa" tra due altre funzioni che tendono allo stesso limite, allora anche la funzione "compressa" tenderà allo stesso limite. * Regola di L'Hôpital: Questa regola si applica quando abbiamo forme indeterminate come 0/0 o ∞/∞. In questi casi, possiamo derivare sia il numeratore che il denominatore e calcolare il limite del rapporto delle derivate.

Esempio di semplificazione algebrica:

Calcoliamo lim_x→2 (x² - 4) / (x - 2).

Se sostituiamo direttamente x = 2, otteniamo 0/0, che è una forma indeterminata.

Possiamo fattorizzare il numeratore come (x + 2)(x - 2).

Quindi, (x² - 4) / (x - 2) = (x + 2)(x - 2) / (x - 2) = x + 2 (per x ≠ 2).

Ora possiamo calcolare il limite sostituendo x = 2: lim_x→2 (x + 2) = 4.

Quando i Limiti Non Esistono

Non tutti i limiti esistono. Un limite può non esistere per diversi motivi:

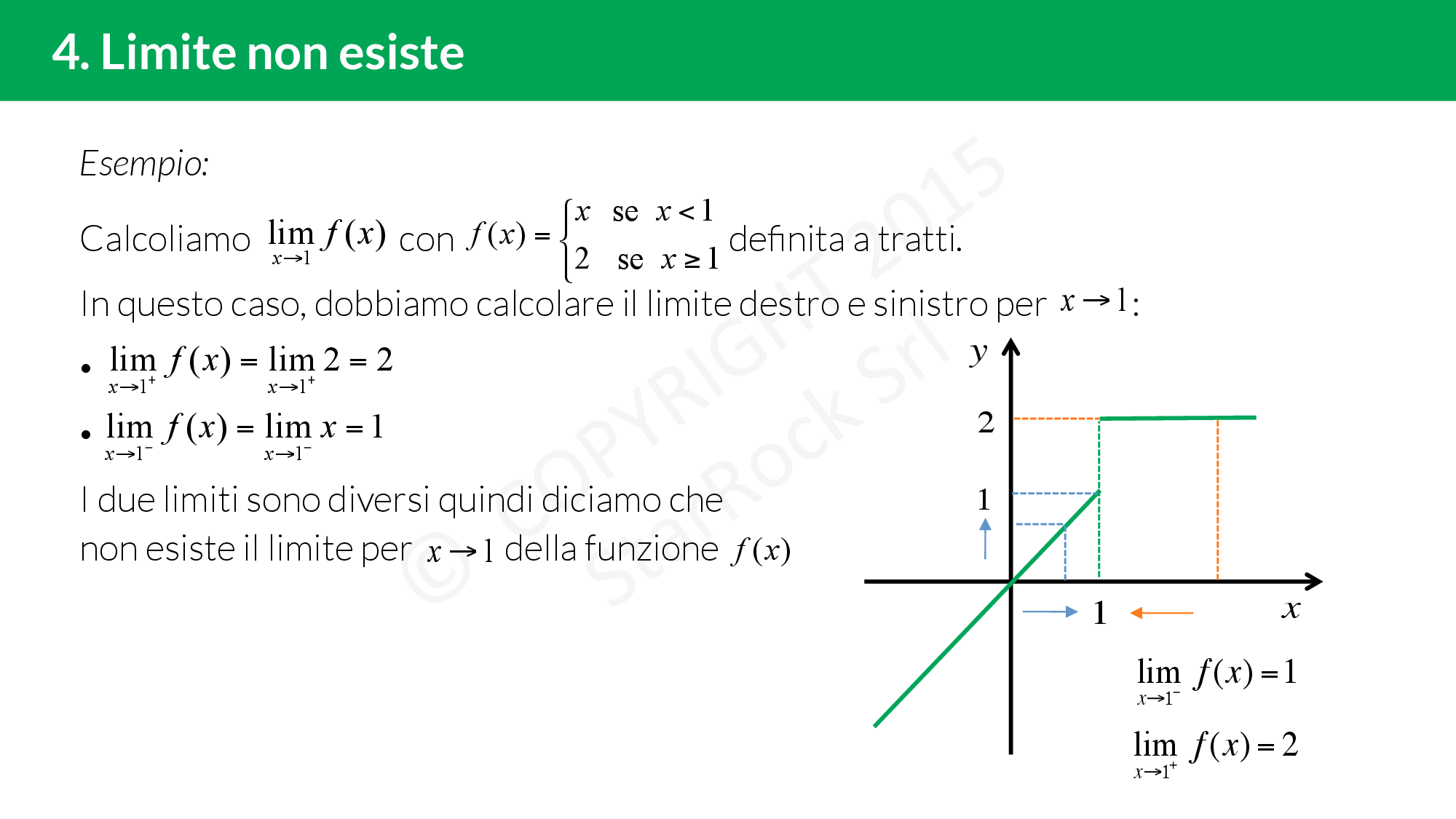
* Limiti laterali diversi: Se il limite da sinistra (x che si avvicina a c da valori inferiori a c) è diverso dal limite da destra (x che si avvicina a c da valori superiori a c), allora il limite non esiste. * Funzione illimitata: Se la funzione cresce o decresce indefinitamente mentre x si avvicina a c, allora il limite non esiste. * Funzione oscillante: Se la funzione oscilla tra due valori mentre x si avvicina a c, allora il limite non esiste.

Esempio di limiti laterali diversi:

Consideriamo la funzione f(x) = |x| / x. Questa funzione è uguale a 1 per x > 0 e -1 per x < 0.

Il limite da destra di f(x) quando x tende a 0 è 1 (lim_x→0⁺ f(x) = 1).

Il limite da sinistra di f(x) quando x tende a 0 è -1 (lim_x→0^- f(x) = -1).

Poiché i limiti laterali sono diversi, il limite di f(x) quando x tende a 0 non esiste.

Consigli Pratici per Imparare i Limiti

Ecco alcuni consigli per affrontare lo studio dei limiti:

* Inizia con gli esempi più semplici: Comprendere i concetti di base è fondamentale. Parti da funzioni semplici e gradualmente aumenta la difficoltà. * Esercitati, esercitati, esercitati: La pratica è la chiave per padroneggiare i limiti. Risolvi molti esercizi diversi per acquisire familiarità con le diverse tecniche. * Visualizza i concetti: Utilizza grafici e diagrammi per visualizzare il comportamento delle funzioni e capire cosa significa un limite. * Chiedi aiuto: Se hai difficoltà, non esitare a chiedere aiuto al tuo insegnante, ai tuoi compagni di classe o a risorse online. * Non scoraggiarti: I limiti possono sembrare complicati all'inizio, ma con la pratica e la perseveranza, diventeranno più chiari e comprensibili.

Ricorda, la comprensione dei limiti è un investimento nel tuo futuro matematico. Ti aprirà le porte a concetti più avanzati e ti fornirà gli strumenti per risolvere problemi complessi in molti campi diversi.

Imparare i limiti è un po' come imparare a guidare: all'inizio può sembrare spaventoso e complicato, ma con la pratica e la pazienza, diventerai un esperto.

Spero che questo articolo ti abbia aiutato a comprendere meglio cosa sono i limiti in matematica. Continua a esplorare e a imparare, e non aver paura di affrontare nuove sfide!