Cos è Un Piano In Geometria
L'idea di un piano è fondamentale in geometria. Si tratta di un concetto astratto che cercheremo di definire e comprendere in questa trattazione, esplorandone le caratteristiche principali e come si manifesta nel mondo che ci circonda.
Definizione e Proprietà Fondamentali
Un piano, in geometria, è una superficie bidimensionale infinita. Immaginatelo come un foglio di carta infinitamente grande che si estende in tutte le direzioni senza mai terminare. Non ha spessore: questa è una caratteristica cruciale. Pensare al piano come a un foglio sottilissimo aiuta a visualizzarlo, ma dobbiamo ricordare che il vero piano è privo di spessore.
Punti e Rette nel Piano
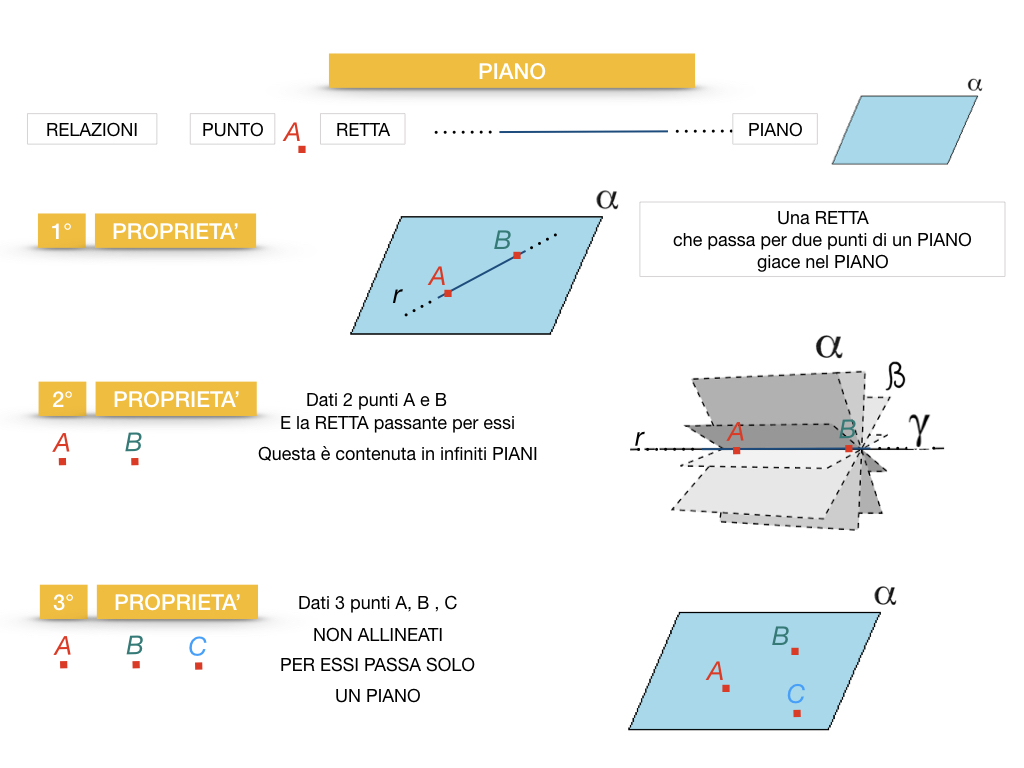
Un piano è composto da infiniti punti. Ogni punto è una posizione specifica nel piano, identificata da coordinate. Allo stesso modo, il piano contiene infinite rette. Una retta è una successione infinita di punti allineati in una stessa direzione. La relazione tra punti, rette e piani è essenziale per la geometria euclidea.
Assiomi Fondamentali
La geometria del piano si basa su alcuni assiomi, ovvero affermazioni considerate vere per definizione. Ad esempio:
- Per due punti distinti passa una e una sola retta.
- Dati una retta e un punto esterno ad essa, esiste una e una sola retta passante per il punto e parallela alla retta data (assioma delle parallele).
Questi assiomi definiscono la struttura del piano e permettono di derivare teoremi e proprietà.
Rappresentazione Analitica
Oltre alla descrizione geometrica, un piano può essere rappresentato analiticamente tramite un'equazione. In uno spazio tridimensionale, un piano è definito da un'equazione lineare del tipo:
ax + by + cz + d = 0
dove a, b, c e d sono costanti reali e x, y e z sono le coordinate di un punto nello spazio. Questa equazione ci permette di manipolare e studiare il piano utilizzando strumenti dell'algebra e dell'analisi.
Relazioni tra Piani
Quando si considerano più piani, possono verificarsi diverse relazioni:
Piani Paralleli
Due piani sono paralleli se non si intersecano mai. In altre parole, non hanno alcun punto in comune. Analiticamente, due piani sono paralleli se i coefficienti a, b, e c delle loro equazioni sono proporzionali.
Piani Perpendicolari
Due piani sono perpendicolari se l'angolo tra essi è di 90 gradi. Analiticamente, due piani sono perpendicolari se il prodotto scalare dei loro vettori normali è zero.
Intersezione di Piani
L'intersezione di due piani non paralleli è una retta. Per trovare l'equazione della retta di intersezione, si risolve il sistema di equazioni dei due piani.
Esempi Reali e Applicazioni
Anche se il piano è un concetto astratto, trova numerose applicazioni nel mondo reale:
Architettura e Ingegneria Civile
I pavimenti, i soffitti e le pareti di un edificio sono approssimazioni di piani. I progetti architettonici utilizzano intensivamente i concetti di piani paralleli, perpendicolari e inclinati per definire la forma e la struttura degli edifici. I software di progettazione assistita (CAD) permettono di manipolare piani e figure geometriche con grande precisione.
Cartografia e Sistemi di Navigazione
Le mappe geografiche sono rappresentazioni bidimensionali della superficie terrestre, che può essere approssimata localmente con un piano. I sistemi di navigazione GPS utilizzano coordinate planimetriche (latitudine e longitudine) per determinare la posizione di un oggetto sulla superficie terrestre. La proiezione di Mercatore, ad esempio, proietta la superficie sferica della Terra su un piano, introducendo distorsioni che devono essere tenute in considerazione.
Grafica Computerizzata e Videogiochi
Nella grafica computerizzata, le immagini sono create componendo figure geometriche, tra cui piani. I piani sono utilizzati per definire le superfici degli oggetti tridimensionali e per calcolare l'illuminazione e le ombre. Nei videogiochi, il terreno è spesso rappresentato come un insieme di piani interconnessi.
Fisica
In fisica, il concetto di piano è utilizzato per studiare il moto di oggetti in due dimensioni, come ad esempio il moto di un proiettile. Anche le onde elettromagnetiche possono essere descritte come onde piane, ovvero onde in cui i campi elettrico e magnetico sono uniformi su piani perpendicolari alla direzione di propagazione.
Oltre la Geometria Euclidea
La geometria che abbiamo descritto finora è la geometria euclidea, basata sugli assiomi di Euclide. Tuttavia, esistono anche altre geometrie, come la geometria non euclidea, in cui l'assioma delle parallele non è valido. In queste geometrie, il concetto di piano assume significati diversi.
Geometria Sferica
Nella geometria sferica, la superficie di una sfera assume il ruolo del piano. Le rette sono sostituite dai cerchi massimi (cerchi che hanno lo stesso raggio della sfera), e l'assioma delle parallele non è valido: non esistono rette parallele su una sfera.
Geometria Iperbolica
Nella geometria iperbolica, esistono infinite rette parallele a una retta data passanti per un punto esterno. Questa geometria ha proprietà molto diverse dalla geometria euclidea e trova applicazioni in diversi campi della matematica e della fisica.
Conclusione
Il piano, pur essendo un concetto astratto, è uno strumento fondamentale per comprendere e descrivere il mondo che ci circonda. Dalla geometria euclidea alla geometria non euclidea, dai progetti architettonici alla grafica computerizzata, il piano è presente in molteplici contesti. Approfondire la conoscenza di questo concetto è essenziale per chiunque si avvicini allo studio della matematica, della fisica, dell'ingegneria e di molte altre discipline.
Per approfondire ulteriormente l'argomento, vi invitiamo a consultare libri di testo di geometria, risorse online e software di geometria dinamica. Sperimentate con diverse costruzioni geometriche, risolvete problemi e cercate di visualizzare il piano in diverse situazioni. La pratica e l'esplorazione sono fondamentali per padroneggiare questo concetto chiave.