Cos è L Asse Di Un Segmento

L'asse di un segmento è un concetto fondamentale della geometria euclidea che riveste un ruolo cruciale in diverse applicazioni pratiche e teoriche. Comprendere a fondo cos'è e come si costruisce è essenziale per chiunque si avvicini allo studio della geometria, sia a livello scolastico che in contesti più avanzati. In questa sede, esploreremo in dettaglio la definizione di asse di un segmento, le sue proprietà principali, i metodi per costruirlo e alcune applicazioni reali.

Definizione e Proprietà Fondamentali

Definizione precisa

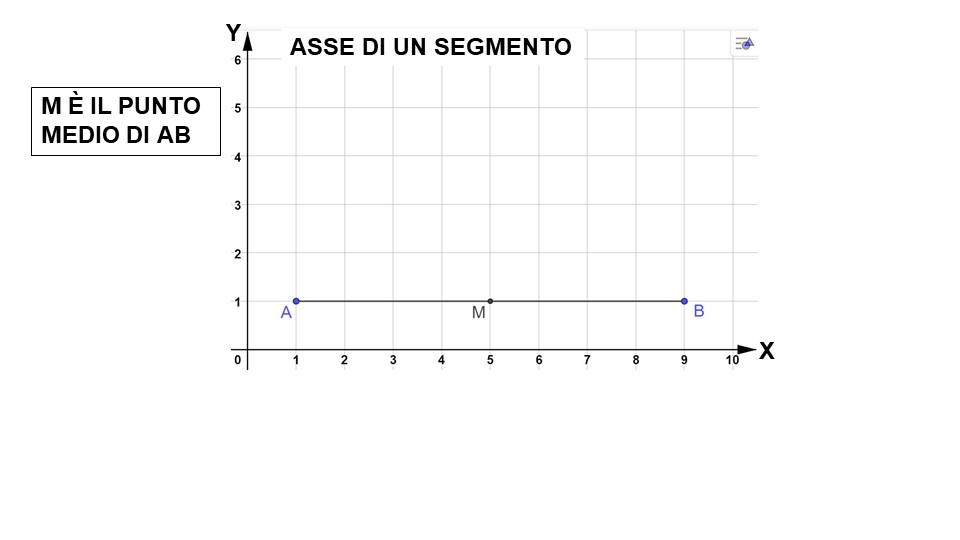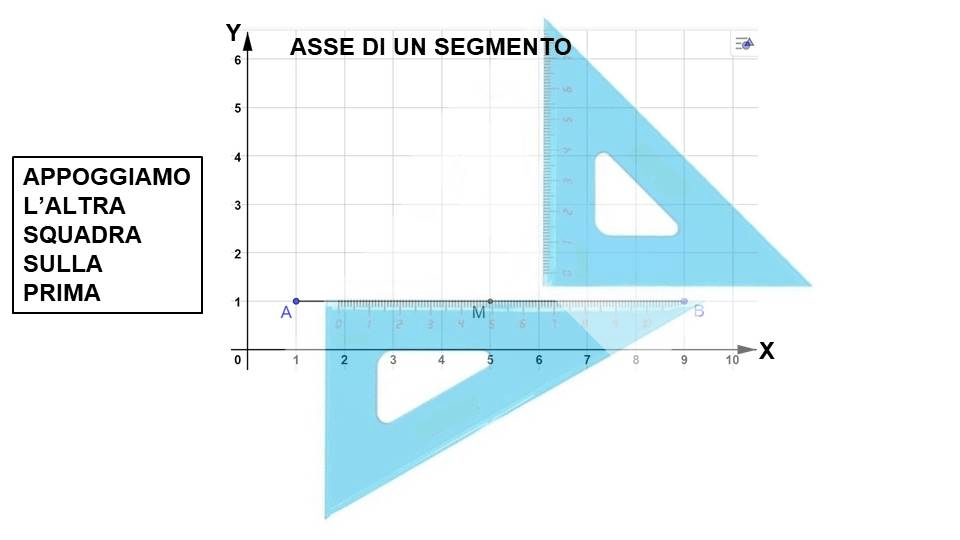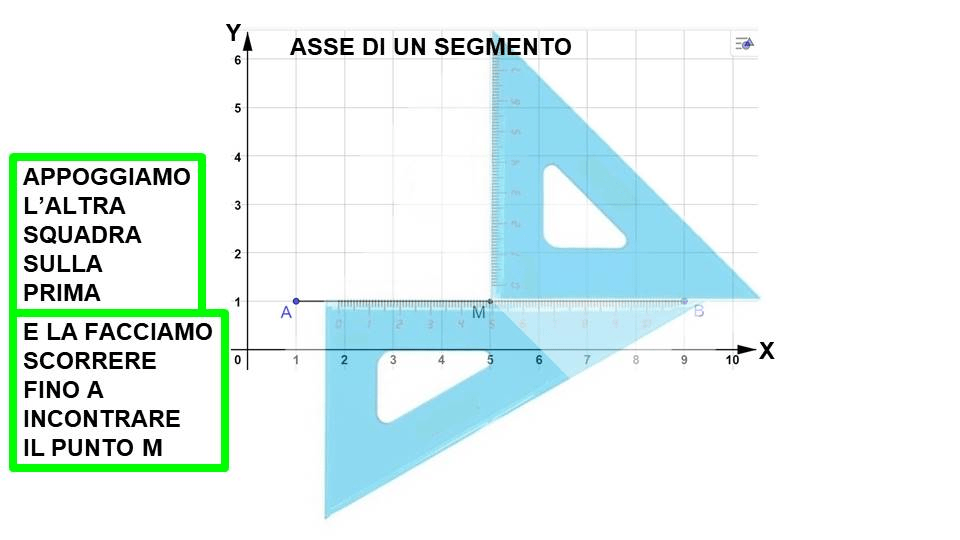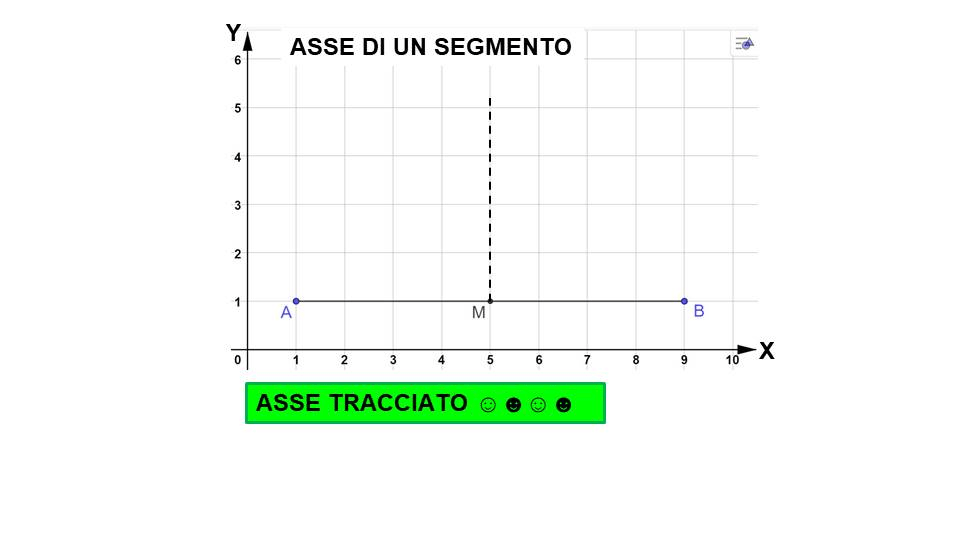
L'asse di un segmento è una retta perpendicolare al segmento considerato e passante per il suo punto medio. Questa definizione implica due caratteristiche essenziali: l'angolo formato tra l'asse e il segmento deve essere di 90 gradi (perpendicolarità), e la retta asse deve dividere il segmento in due parti uguali (passaggio per il punto medio).

Proprietà cruciali

La proprietà più importante dell'asse di un segmento è che ogni punto sull'asse è equidistante dagli estremi del segmento. Questo significa che se prendiamo un qualsiasi punto P sull'asse del segmento AB, la distanza tra P e A (PA) è uguale alla distanza tra P e B (PB). Questa proprietà è fondamentale per dimostrare diverse costruzioni geometriche e risolvere problemi.

Dimostrazione della proprietà: Consideriamo il segmento AB e il suo asse r. Sia M il punto medio di AB (e quindi il punto di intersezione tra AB e r). Prendiamo un punto P qualsiasi su r. Vogliamo dimostrare che PA = PB. Consideriamo i triangoli PMA e PMB. Essi hanno: * AM = MB (M è il punto medio di AB) * PM è in comune * Angolo PMA = Angolo PMB = 90° (r è perpendicolare ad AB) Quindi, per il primo criterio di congruenza dei triangoli (lato-angolo-lato), i triangoli PMA e PMB sono congruenti. Di conseguenza, PA = PB, come volevamo dimostrare.

Unicità dell'asse

Per un dato segmento, esiste un solo asse. Non ci possono essere due rette diverse che siano contemporaneamente perpendicolari al segmento e passanti per il suo punto medio. Questo deriva dalla geometria euclidea e dalla definizione stessa di perpendicolarità e punto medio.

Costruzione dell'Asse di un Segmento

Metodo con riga e compasso

Il metodo classico per costruire l'asse di un segmento è quello che utilizza riga e compasso. Ecco i passaggi:

1. Dato il segmento AB, puntare il compasso in A con un'apertura maggiore della metà della lunghezza di AB. Tracciare un arco che si estende sopra e sotto il segmento.
2. Mantenendo la stessa apertura del compasso, puntare il compasso in B e tracciare un altro arco che interseca il primo arco in due punti. Chiamiamo questi punti C e D.
3. Tracciare la retta passante per i punti C e D. Questa retta è l'asse del segmento AB.

Giustificazione della costruzione: I punti C e D, essendo ottenuti intersecando archi di uguale raggio centrati in A e B, sono equidistanti da A e B. Pertanto, sia C che D appartengono all'asse del segmento AB. Poiché per due punti passa una e una sola retta, la retta CD è l'asse di AB.

Metodo analitico (nel piano cartesiano)

Se il segmento AB è definito in un piano cartesiano tramite le coordinate dei suoi estremi A(x_A, y_A) e B(x_B, y_B), possiamo determinare l'equazione dell'asse analiticamente.

1. Calcolare il punto medio M del segmento AB: M((x_A + x_B)/2, (y_A + y_B)/2).
2. Calcolare il coefficiente angolare m del segmento AB: m = (y_B - y_A) / (x_B - x_A).
3. Calcolare il coefficiente angolare m' dell'asse, che è l'antireciproco di m: m' = -1/m. (Se m=0, l'asse è una retta verticale di equazione x = (x_A + x_B)/2. Se x_A = x_B, l'asse è una retta orizzontale di equazione y = (y_A + y_B)/2.)
4. Utilizzare l'equazione della retta passante per un punto con coefficiente angolare noto (forma punto-pendenza): y - y_M = m'(x - x_M), dove (x_M, y_M) sono le coordinate del punto medio M.

Semplificando l'equazione ottenuta, si otterrà l'equazione cartesiana dell'asse del segmento AB nella forma y = m'x + q, dove q è l'intercetta.

Applicazioni Reali e Esempi Pratici

Geometria e costruzioni geometriche

L'asse di un segmento è fondamentale per la costruzione di diverse figure geometriche, come triangoli isosceli e circonferenze circoscritte. Ad esempio, il circocentro di un triangolo (il centro della circonferenza circoscritta) è il punto di incontro degli assi dei lati del triangolo. Questa proprietà è cruciale in problemi di geometria e nella risoluzione di esercizi.

Ingegneria e architettura

In ingegneria e architettura, la perpendicolarità e l'equidistanza associate all'asse di un segmento sono utilizzate per garantire la simmetria e la stabilità delle strutture. Ad esempio, nella progettazione di ponti e edifici, l'asse può essere utilizzato per definire l'asse di simmetria di una campata o di un elemento strutturale, assicurando che i carichi siano distribuiti uniformemente.

Cartografia e navigazione

In cartografia e navigazione, il concetto di asse può essere applicato per determinare la posizione relativa di punti e oggetti. Ad esempio, se si conoscono le coordinate di due punti di riferimento, si può calcolare l'asse del segmento che li congiunge per determinare una linea di posizione (LOP) equidistante da entrambi i punti. Questo è particolarmente utile in situazioni in cui la precisione della localizzazione è critica.

Grafica computerizzata e modellazione 3D

Nella grafica computerizzata e nella modellazione 3D, l'asse di un segmento è utilizzato per creare simmetrie e riflessioni di oggetti. Ad esempio, per riflettere un oggetto rispetto a una retta, si può considerare l'asse del segmento che congiunge un punto dell'oggetto con la sua immagine riflessa. Questo è fondamentale per creare modelli 3D realistici e per realizzare animazioni complesse.

Esempio numerico

Consideriamo i punti A(1, 2) e B(5, 4) nel piano cartesiano. Calcoliamo l'asse del segmento AB.

1. Punto medio M: M((1+5)/2, (2+4)/2) = M(3, 3)
2. Coefficiente angolare m di AB: m = (4-2)/(5-1) = 2/4 = 1/2
3. Coefficiente angolare m' dell'asse: m' = -1/(1/2) = -2
4. Equazione dell'asse: y - 3 = -2(x - 3) => y - 3 = -2x + 6 => y = -2x + 9

Quindi l'equazione dell'asse del segmento AB è y = -2x + 9.

Conclusioni

L'asse di un segmento è un concetto geometrico apparentemente semplice, ma le sue proprietà e applicazioni sono sorprendentemente vaste e significative. Dalla costruzione di figure geometriche complesse alla risoluzione di problemi di ingegneria, architettura, cartografia e grafica computerizzata, l'asse di un segmento si rivela uno strumento potente e versatile. Comprendere a fondo la sua definizione, le sue proprietà e i metodi per costruirlo è fondamentale per chiunque si interessi alla geometria e alle sue applicazioni pratiche.

Invitiamo il lettore a sperimentare con la costruzione dell'asse di un segmento utilizzando riga e compasso, a calcolarne l'equazione nel piano cartesiano e a cercare altre applicazioni reali in diversi ambiti. L'esplorazione attiva e la sperimentazione sono i migliori modi per consolidare la comprensione di questo importante concetto geometrico.