Cos è L Asse Di Simmetria

Quante volte, osservando un fiore, una farfalla o persino il nostro viso, abbiamo notato una certa armonia, un equilibrio quasi perfetto? Spesso, questa sensazione di equilibrio deriva dalla presenza di un elemento fondamentale nella geometria e nell'arte: l'asse di simmetria. Questo articolo è rivolto a tutti coloro che, curiosi di esplorare il mondo della matematica e del design, desiderano comprendere a fondo cos'è l'asse di simmetria, come identificarlo e perché è così importante.

Cos'è l'Asse di Simmetria? Una Definizione Chiara

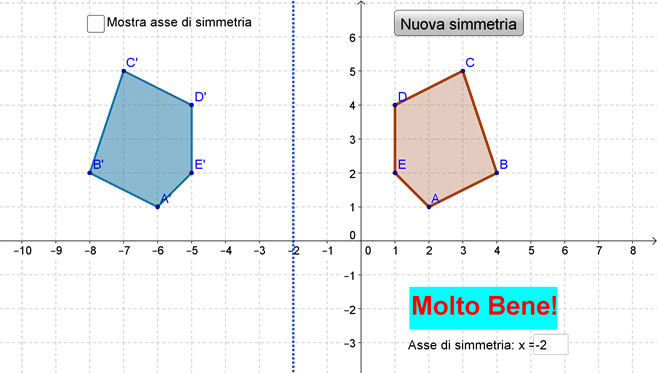
L'asse di simmetria, in termini semplici, è una linea immaginaria che divide una figura in due parti identiche, speculari. Immagina di piegare la figura lungo questa linea: le due metà dovrebbero combaciare perfettamente. Questa "piega" è, appunto, l'asse di simmetria.

Più formalmente, possiamo dire che una figura possiede un asse di simmetria se esiste una retta tale che, riflettendo la figura rispetto a questa retta, si ottiene la figura originale. In altre parole, la figura rimane invariata dopo una riflessione rispetto all'asse di simmetria.

Tipi di Simmetria: Assiale e Centrale

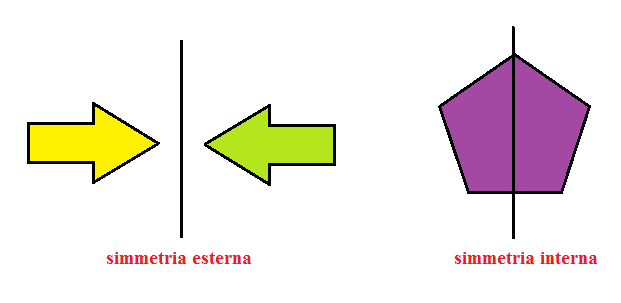
È importante distinguere tra due tipi principali di simmetria:

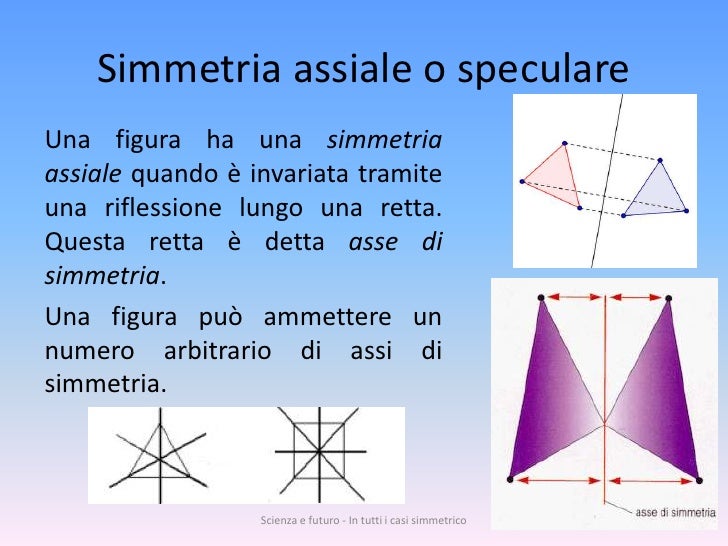
• Simmetria Assiale (o Riflessione): Quella di cui stiamo parlando principalmente, dove l'asse di simmetria è una retta.
• Simmetria Centrale (o Rotazione di 180°): In questo caso, esiste un punto (il centro di simmetria) tale che, ruotando la figura di 180° attorno a questo punto, si ottiene la figura originale. Ad esempio, un parallelogramma ha simmetria centrale, ma non assiale.

In questo articolo ci concentreremo sulla simmetria assiale e sull'asse di simmetria che la definisce.

Come Trovare l'Asse di Simmetria: Metodi e Trucchi

Identificare l'asse di simmetria di una figura può sembrare complicato, ma con un po' di pratica diventa intuitivo. Ecco alcuni metodi e trucchi:

• Osservazione Visiva: Inizia guardando attentamente la figura. Cerca una linea che sembri dividerla in due metà identiche.
• Piegatura Immaginaria: Immagina di piegare la figura lungo una linea. Le due metà combaciano? Se sì, quella è probabilmente un asse di simmetria.
• Riflessione: Visualizza la figura riflessa rispetto a una linea. Se l'immagine riflessa coincide con la figura originale, quella è un asse di simmetria.
• Utilizzo di uno Specchio: Posiziona uno specchio lungo una linea sulla figura. Se l'immagine nello specchio, combinata con la parte visibile della figura, crea l'intera figura, allora lo specchio è posizionato lungo un asse di simmetria.

Esempi Pratici: Identificare l'Asse di Simmetria in Diverse Figure

Vediamo alcuni esempi per chiarire meglio il concetto:

• Quadrato: Ha quattro assi di simmetria: due che passano per i punti medi dei lati opposti e due che coincidono con le diagonali.
• Rettangolo: Ha due assi di simmetria: quelli che passano per i punti medi dei lati opposti.
• Cerchio: Ha infiniti assi di simmetria: qualsiasi retta che passa per il centro del cerchio è un asse di simmetria.
• Triangolo Equilatero: Ha tre assi di simmetria: ognuno passa per un vertice e per il punto medio del lato opposto.
• Triangolo Isoscele: Ha un solo asse di simmetria: quello che passa per il vertice opposto alla base e per il punto medio della base.
• Lettere dell'Alfabeto: Alcune lettere hanno assi di simmetria. Ad esempio, la A ha un asse di simmetria verticale, la H ne ha uno verticale e uno orizzontale, mentre la B ha un asse di simmetria orizzontale.

Attenzione: Non tutte le figure hanno un asse di simmetria! Ad esempio, un triangolo scaleno (con tutti i lati di lunghezza diversa) non ne ha nessuno.

L'Importanza dell'Asse di Simmetria: Oltre la Geometria

L'asse di simmetria non è solo un concetto teorico; ha applicazioni pratiche in molti campi:

• Architettura: Molti edifici sono progettati con un asse di simmetria per creare un senso di equilibrio ed armonia. Pensa al Taj Mahal o a molte cattedrali gotiche.
• Design: L'asse di simmetria è fondamentale nel design di oggetti, loghi, tessuti e molto altro. Un design simmetrico è spesso percepito come più piacevole e ordinato.
• Arte: Molti artisti utilizzano la simmetria per creare opere visivamente accattivanti. Pensa alle opere di Leonardo da Vinci o alle decorazioni geometriche islamiche.
• Biologia: Molti organismi viventi, come farfalle, fiori e persino il corpo umano (almeno esternamente), mostrano una simmetria approssimativa rispetto a un asse centrale.
• Matematica: La simmetria è un concetto fondamentale in molti rami della matematica, come la geometria, l'algebra e la teoria dei gruppi.

Simmetria nella Natura: Un Esempio Toccante

Osserva un fiocco di neve. La sua forma esagonale e la sua intricata struttura sono un perfetto esempio di simmetria nella natura. Ogni ramo del fiocco di neve è identico agli altri, riflettendo l'ordine intrinseco del mondo naturale. La simmetria, in questo caso, è il risultato delle leggi fisiche che governano la formazione dei cristalli di ghiaccio.

Asse di Simmetria e Funzioni Matematiche

L'asse di simmetria trova un'applicazione importante anche nello studio delle funzioni matematiche, in particolare delle funzioni pari. Una funzione f(x) è detta pari se f(x) = f(-x) per ogni valore di x nel dominio della funzione. Graficamente, questo significa che il grafico della funzione è simmetrico rispetto all'asse y (l'asse delle ordinate). L'asse y è quindi l'asse di simmetria del grafico di una funzione pari.

Esempi di funzioni pari includono:

• f(x) = x²
• f(x) = cos(x)
• f(x) = |x| (valore assoluto di x)

Comprendere la simmetria di una funzione può semplificare notevolmente lo studio del suo grafico e delle sue proprietà.

Perché Dovremmo Preoccuparci dell'Asse di Simmetria?

Comprendere l'asse di simmetria non è solo un esercizio di geometria. È un modo per sviluppare il nostro senso estetico, per apprezzare l'ordine e l'armonia che ci circondano. Che tu sia un artista, un designer, uno studente di matematica o semplicemente una persona curiosa, la conoscenza dell'asse di simmetria può arricchire la tua comprensione del mondo e migliorare la tua capacità di apprezzare la bellezza in tutte le sue forme.

Inoltre, la capacità di identificare e comprendere la simmetria può migliorare le tue capacità di problem-solving in diversi ambiti. Ad esempio, in geometria, riconoscere la simmetria di una figura può aiutarti a risolvere problemi più rapidamente e facilmente. Nel design, la comprensione della simmetria ti permette di creare composizioni più equilibrate e piacevoli alla vista.

Conclusione: Un Mondo di Simmetria da Esplorare

L'asse di simmetria è molto più di una semplice linea immaginaria. È una chiave per comprendere l'armonia e l'equilibrio che permeano il mondo che ci circonda. Che tu stia ammirando un'opera d'arte, progettando un logo o semplicemente osservando la natura, la consapevolezza dell'asse di simmetria ti permetterà di vedere il mondo con occhi nuovi. Quindi, la prossima volta che ti imbatti in una figura, prenditi un momento per cercare il suo asse di simmetria. Potresti rimanere sorpreso da ciò che scopri!