Condizione Necessaria Per La Convergenza Di Una Serie

L'analisi delle serie numeriche è un pilastro fondamentale del calcolo infinitesimale, con applicazioni che spaziano dalla fisica all'ingegneria, dall'economia all'informatica. Comprendere il comportamento delle serie, in particolare se convergono o divergono, è cruciale per risolvere problemi complessi e modellare fenomeni reali. Un concetto chiave in questo contesto è la condizione necessaria per la convergenza. Questo articolo esplorerà questa condizione in dettaglio, analizzando il suo significato, le sue implicazioni e i suoi limiti, fornendo esempi e contestualizzandola con casi reali.

La Condizione Necessaria: Il Limite del Termine Generale

La condizione necessaria per la convergenza di una serie afferma che, se una serie converge, allora il limite del suo termine generale deve essere zero. Formalmente, sia Σ_n=1^∞ a_n una serie numerica. Se Σ_n=1^∞ a_n converge, allora lim_n→∞ a_n = 0.

È fondamentale sottolineare che questa è una condizione *necessaria* ma non *sufficiente*. Questo significa che se il limite del termine generale non è zero, allora la serie *sicuramente* diverge. Tuttavia, se il limite del termine generale è zero, non possiamo concludere automaticamente che la serie converge; sono necessari ulteriori test e analisi.

Dimostrazione della Condizione Necessaria

La dimostrazione di questa condizione è piuttosto elegante e si basa sulla definizione di convergenza di una serie. Sia S_n la somma parziale n-esima della serie, definita come S_n = a₁ + a₂ + ... + a_n. Se la serie converge a un valore S, allora lim_n→∞ S_n = S.

Consideriamo ora la somma parziale S_n-1. Poiché la serie converge, anche lim_n→∞ S_n-1 = S. Quindi, abbiamo:

a_n = S_n - S_n-1

Prendendo il limite per n che tende a infinito di entrambi i lati, otteniamo:

lim_n→∞ a_n = lim_n→∞ (S_n - S_n-1) = lim_n→∞ S_n - lim_n→∞ S_n-1 = S - S = 0

Questo dimostra che se la serie converge, il limite del termine generale deve essere zero.

Implicazioni Pratiche e Controesempi

La condizione necessaria fornisce un test rapido e semplice per escludere la convergenza di una serie. Se si calcola il limite del termine generale e si trova che è diverso da zero, si può immediatamente concludere che la serie diverge, senza bisogno di ulteriori analisi. Questo può risparmiare tempo e sforzi significativi.

Tuttavia, come accennato, la condizione non è sufficiente. Un esempio classico è la serie armonica, Σ_n=1^∞ 1/n. In questo caso, lim_n→∞ 1/n = 0, ma la serie armonica *diverge*. Questo dimostra chiaramente che il fatto che il limite del termine generale sia zero non implica necessariamente la convergenza della serie.

Altri Esempi e Tecniche di Valutazione

Consideriamo la serie Σ_n=1^∞ n/(n+1). Calcoliamo il limite del termine generale: lim_n→∞ n/(n+1) = 1. Poiché il limite è diverso da zero, la serie diverge per la condizione necessaria.

Un altro esempio è la serie Σ_n=1^∞ (-1)ⁿ. In questo caso, il limite del termine generale non esiste (oscilla tra -1 e 1). Pertanto, la serie diverge.

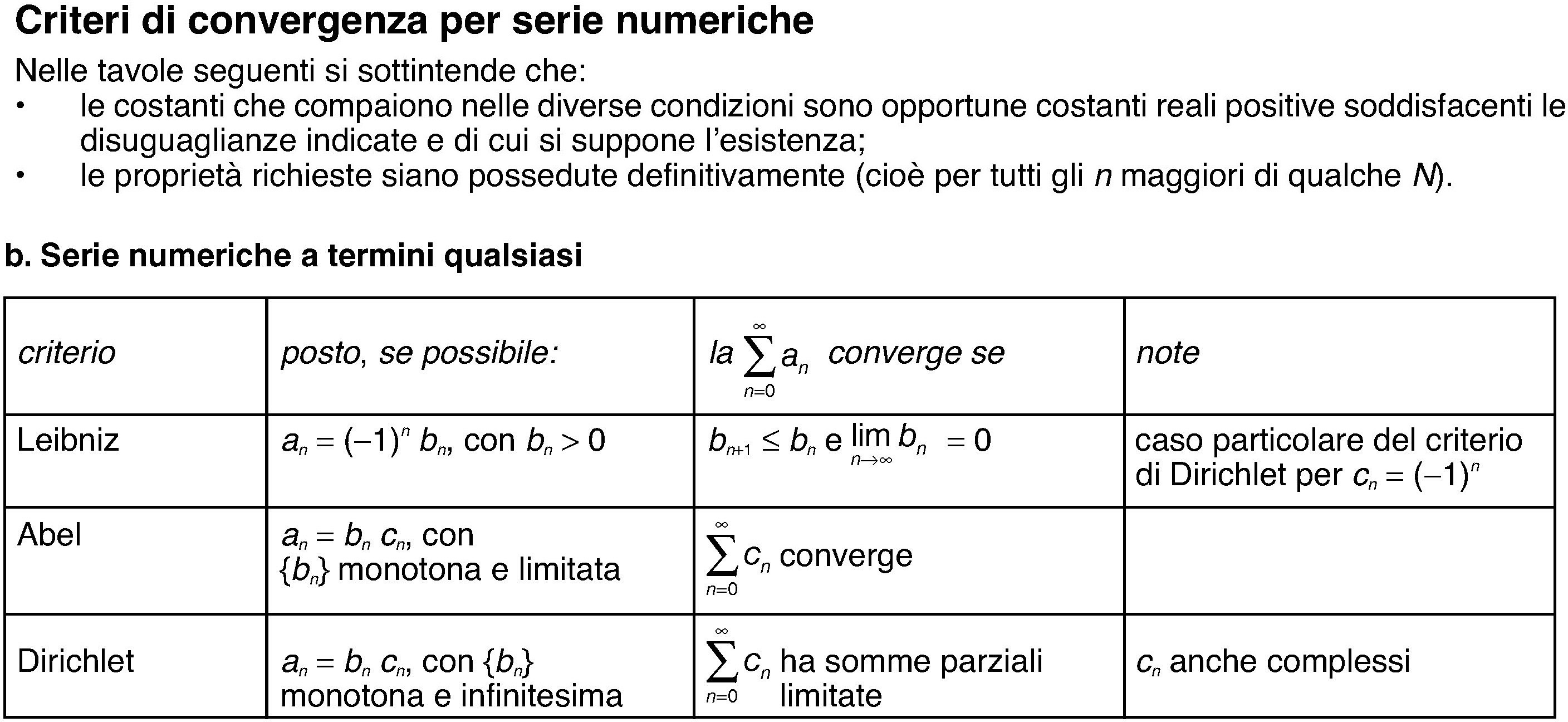
Per serie dove il limite del termine generale è zero, è necessario ricorrere ad altri test di convergenza, come:

Test del Rapporto: Utile per serie con termini che coinvolgono fattoriali o potenze.
Test della Radice: Simile al test del rapporto, ma spesso più facile da applicare.
Test dell'Integrale: Mette in relazione la convergenza della serie con la convergenza di un integrale improprio.
Test di Confronto: Confronta la serie con un'altra serie di cui si conosce il comportamento.
Test delle Serie Alternate: Specifico per serie in cui i termini alternano segno.

Applicazioni nel Mondo Reale

Le serie numeriche, e quindi la loro convergenza, sono fondamentali in molte discipline. Ad esempio:

Fisica: Le serie di Fourier sono utilizzate per rappresentare segnali periodici e risolvere equazioni differenziali che descrivono fenomeni fisici come onde sonore e vibrazioni. La convergenza di queste serie è cruciale per ottenere rappresentazioni accurate.
Ingegneria: Le serie di Taylor e Maclaurin sono usate per approssimare funzioni complesse con polinomi, semplificando i calcoli e le simulazioni. La convergenza di queste serie determina l'accuratezza dell'approssimazione.
Economia: Le serie geometriche sono utilizzate per calcolare il valore attuale di flussi di cassa futuri e per analizzare modelli di crescita economica. La convergenza di queste serie è essenziale per ottenere risultati finanziari significativi.
Informatica: Le serie sono utilizzate in algoritmi di calcolo numerico, compressione dati e crittografia. La convergenza degli algoritmi garantisce che i risultati siano accurati e affidabili.

Ad esempio, nel campo della finanza, il calcolo del valore attuale di una rendita perpetua si basa sulla convergenza di una serie geometrica. Se la serie non convergesse, il valore attuale sarebbe infinito, rendendo il calcolo privo di significato.

Limitazioni e Considerazioni Aggiuntive

È importante ricordare che la condizione necessaria per la convergenza è solo un punto di partenza. Una volta verificato che il limite del termine generale è zero, è necessario utilizzare altri test per determinare la convergenza effettiva della serie. La scelta del test appropriato dipende dalla forma del termine generale e dalle proprietà della serie.

Inoltre, è cruciale prestare attenzione alla velocità di convergenza. Anche se una serie converge, potrebbe farlo molto lentamente, il che significa che è necessario sommare un gran numero di termini per ottenere un'approssimazione accurata della somma. In questi casi, possono essere utilizzate tecniche di accelerazione della convergenza per migliorare l'efficienza dei calcoli.

In alcuni casi, può essere utile studiare la convergenza assoluta di una serie. Una serie Σ_n=1^∞ a_n converge assolutamente se la serie Σ_n=1^∞ |a_n| converge. Se una serie converge assolutamente, allora converge anche semplicemente. Tuttavia, il contrario non è sempre vero (vedi la serie armonica alternata).

Conclusione

La condizione necessaria per la convergenza di una serie è uno strumento fondamentale nell'analisi delle serie numeriche. Permette di escludere rapidamente la convergenza di una serie se il limite del suo termine generale non è zero. Pur essendo una condizione necessaria, non è sufficiente, e quindi è essenziale utilizzare altri test di convergenza per determinare il comportamento completo della serie.

Comprendere la condizione necessaria e i suoi limiti è cruciale per chiunque lavori con le serie numeriche, in quanto fornisce una base solida per l'analisi e la risoluzione di problemi in una vasta gamma di discipline. Invitiamo i lettori a esercitarsi con diversi esempi e a esplorare i vari test di convergenza per approfondire la loro comprensione di questo importante concetto.