Come Trovare Q In Una Retta

Nel mondo della matematica, e in particolare in geometria analitica, una delle sfide più comuni è comprendere e manipolare le equazioni delle rette. Un elemento cruciale di queste equazioni è il termine "q", noto anche come intercetta o termine noto. Comprendere come trovare "q" è fondamentale per analizzare, interpretare e applicare le rette in una vasta gamma di contesti.
Comprendere l'Equazione di una Retta
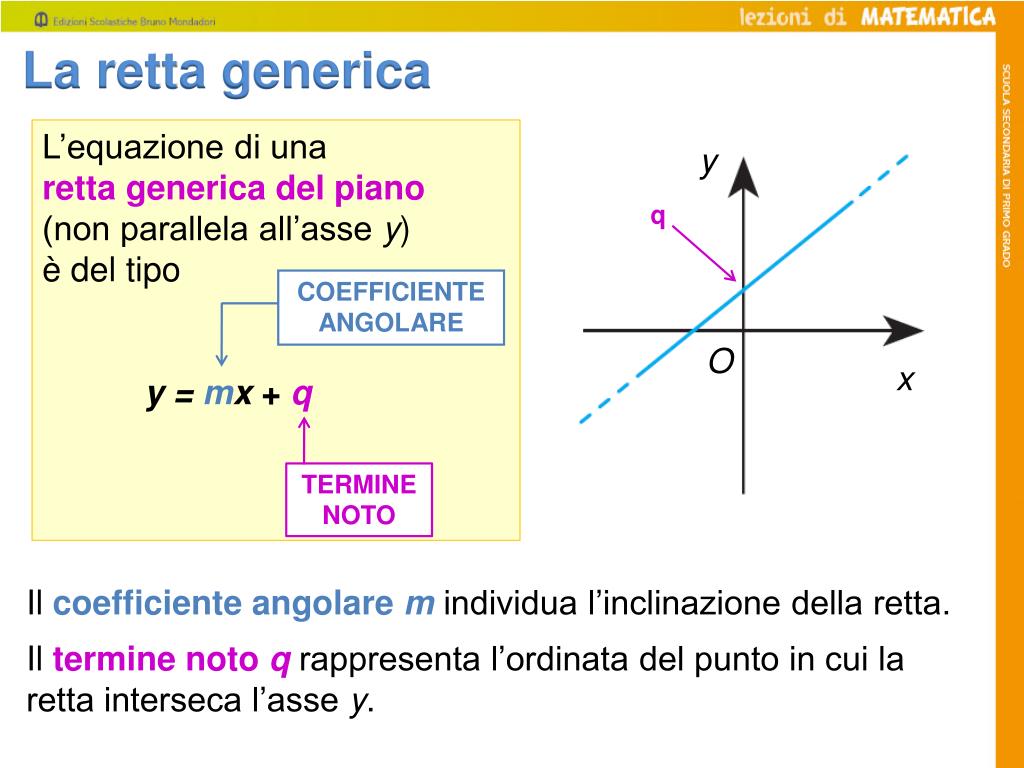
Prima di addentrarci nei metodi per trovare "q", è essenziale avere una solida comprensione dell'equazione di una retta. La forma più comune è la forma esplicita:
y = mx + q
Dove:
- y rappresenta l'ordinata (il valore sull'asse verticale).
- x rappresenta l'ascissa (il valore sull'asse orizzontale).
- m rappresenta il coefficiente angolare, ovvero la pendenza della retta.
- q rappresenta l'intercetta o termine noto, ovvero il punto in cui la retta interseca l'asse y.
L'intercetta "q" indica il valore di 'y' quando 'x' è zero. In altre parole, è l'altezza della retta sull'asse y.
Metodi per Trovare "q"
Esistono diversi metodi per determinare il valore di "q" in un'equazione di una retta. La scelta del metodo dipende dalle informazioni a nostra disposizione.
1. Conoscendo il Coefficiente Angolare (m) e un Punto (x, y)
Questo è probabilmente il metodo più comune. Se conosciamo il coefficiente angolare 'm' della retta e le coordinate di un punto (x, y) che giace sulla retta, possiamo facilmente calcolare "q".
La formula è derivata direttamente dall'equazione esplicita:
q = y - mx
Esempio:
Supponiamo di avere una retta con coefficiente angolare m = 2 e che passi per il punto (3, 7). Per trovare "q", sostituiamo i valori nell'equazione:
q = 7 - (2 * 3)
q = 7 - 6
q = 1
Quindi, l'equazione della retta è y = 2x + 1, e l'intercetta è q = 1.
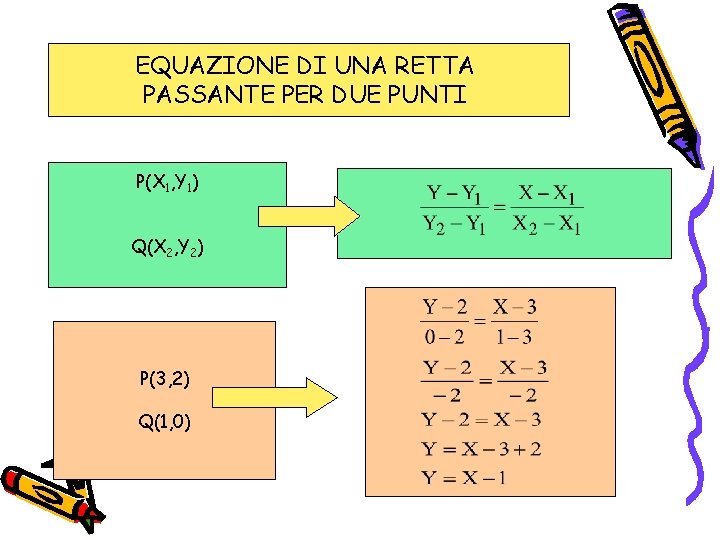
2. Conoscendo Due Punti (x₁, y₁) e (x₂, y₂)
Se conosciamo le coordinate di due punti sulla retta, possiamo trovare "q" in due passaggi:
- Calcolare il coefficiente angolare 'm': La formula per calcolare 'm' è:
m = (y₂ - y₁) / (x₂ - x₁)
- Utilizzare uno dei due punti e il valore di 'm' per calcolare 'q': Scegli uno dei due punti (ad esempio, (x₁, y₁)) e sostituisci i valori nell'equazione q = y₁ - mx₁
Esempio:
Supponiamo di avere due punti: (1, 3) e (4, 9).
- Calcolare 'm':
m = (9 - 3) / (4 - 1)
m = 6 / 3
m = 2
- Calcolare 'q': Usiamo il punto (1, 3):
q = 3 - (2 * 1)
q = 3 - 2
q = 1
Quindi, l'equazione della retta è y = 2x + 1, e l'intercetta è q = 1.
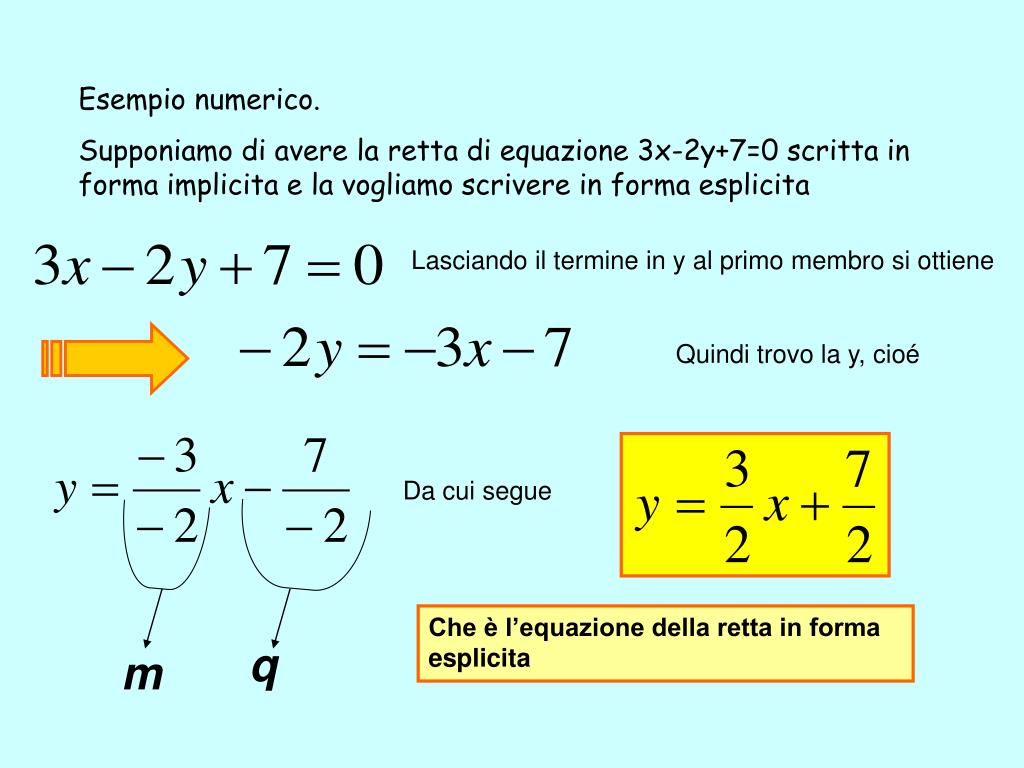
3. Dall'Equazione Implicita della Retta
A volte, l'equazione della retta è data in forma implicita:
Ax + By + C = 0
Per trovare "q", dobbiamo trasformare l'equazione nella forma esplicita (y = mx + q). Questo si fa isolando 'y':
- Sottrarre Ax e C da entrambi i lati: By = -Ax - C
- Dividere entrambi i lati per B: y = (-A/B)x - (C/B)
Ora l'equazione è nella forma esplicita. Il coefficiente angolare è m = -A/B e l'intercetta è q = -C/B.
Esempio:
Supponiamo di avere l'equazione 2x + 3y - 6 = 0.
- Isolare 'y': 3y = -2x + 6
- Dividere per 3: y = (-2/3)x + 2
Quindi, l'intercetta è q = 2.
4. Dalla Rappresentazione Grafica
Se abbiamo la rappresentazione grafica della retta, trovare "q" è molto semplice. Basta identificare il punto in cui la retta interseca l'asse y. La coordinata y di quel punto è il valore di "q". Questo metodo è particolarmente utile quando si lavora con grafici o diagrammi.
Esempio:
Se osserviamo un grafico e notiamo che la retta interseca l'asse y nel punto (0, 4), allora l'intercetta è q = 4.
Applicazioni Reali
La capacità di determinare "q" è fondamentale in molti contesti del mondo reale:
- Finanza: In modelli lineari che rappresentano costi e ricavi, "q" può rappresentare i costi fissi. Ad esempio, se un'azienda ha costi fissi di 10.000€ e un costo variabile per unità di 5€, l'equazione del costo totale potrebbe essere C = 5x + 10000, dove q = 10000 rappresenta i costi fissi.
- Fisica: In cinematica, se la velocità di un oggetto aumenta linearmente nel tempo, "q" può rappresentare la velocità iniziale. Ad esempio, se la velocità di un'auto aumenta di 2 m/s ogni secondo e la sua velocità iniziale è di 10 m/s, l'equazione della velocità nel tempo potrebbe essere v = 2t + 10, dove q = 10 rappresenta la velocità iniziale.
- Statistica: Nell'analisi di regressione lineare, "q" rappresenta l'intercetta della retta di regressione, ovvero il valore previsto della variabile dipendente quando la variabile indipendente è zero.
- Ingegneria: Nel progettare sistemi lineari, come circuiti elettrici o sistemi meccanici, "q" può rappresentare un valore di offset o un termine costante che influenza il comportamento del sistema.
Esempio di dati reali:
Immaginiamo di analizzare i dati di vendita di un prodotto. Abbiamo i seguenti dati:
| Spesa pubblicitaria (€) (x) | Vendite (€) (y) |
|---|---|
| 1000 | 5000 |
| 2000 | 8000 |
Possiamo utilizzare questi dati per creare una retta di regressione lineare. Calcolando 'm' otteniamo:
m = (8000 - 5000) / (2000 - 1000) = 3
Quindi, usando il punto (1000, 5000) e 'm' = 3, calcoliamo 'q':
q = 5000 - (3 * 1000) = 2000
L'equazione della retta è y = 3x + 2000. Questo significa che, anche senza alcuna spesa pubblicitaria (x = 0), ci aspetteremmo vendite per 2000€ (q = 2000). Questo potrebbe rappresentare vendite dovute a fattori come la notorietà del marchio o il passaparola.
Conclusioni
La determinazione di "q" (l'intercetta) in un'equazione di una retta è un'abilità fondamentale con applicazioni pratiche in una vasta gamma di discipline. Che tu stia lavorando con dati finanziari, modelli fisici o analisi statistiche, comprendere come trovare "q" ti fornirà uno strumento potente per interpretare e manipolare relazioni lineari.
Ricorda che esistono diversi metodi per trovare "q", e la scelta del metodo dipende dalle informazioni disponibili. Padronizzare questi metodi ti permetterà di affrontare con sicurezza problemi che coinvolgono rette e equazioni lineari.
Esercitati! La pratica è la chiave per padroneggiare qualsiasi concetto matematico. Prova a risolvere diversi esercizi e problemi che richiedono di trovare "q" in varie situazioni. Più ti eserciterai, più diventerai abile e sicuro nell'uso di queste tecniche. Cerca online esercizi e problemi di geometria analitica riguardanti rette e intercette per migliorare ulteriormente le tue competenze.