Come Trovare M Di Una Retta

Capita a tutti, prima o poi, di trovarsi di fronte a un problema di geometria analitica che ci fa grattare la testa. Magari dobbiamo progettare un piccolo orto sul nostro balcone e capire l'inclinazione ideale per massimizzare l'esposizione al sole, oppure stiamo cercando di simulare la traiettoria di una pallina da golf in un videogioco. In questi casi, comprendere come trovare la 'm' di una retta, ovvero il suo coefficiente angolare, diventa cruciale. Non è solo un esercizio scolastico, ma uno strumento potente per risolvere problemi concreti.

Spesso, la matematica viene percepita come un ostacolo insormontabile, piena di formule astruse e concetti incomprensibili. Ma la verità è che dietro ogni formula c'è una logica, un modo per descrivere il mondo che ci circonda. E la 'm' di una retta non fa eccezione. Cercheremo di rendere questo concetto il più accessibile possibile, usando esempi pratici e un linguaggio chiaro, per darti gli strumenti necessari a superare questa sfida.

Cos'è esattamente la 'm' di una retta?

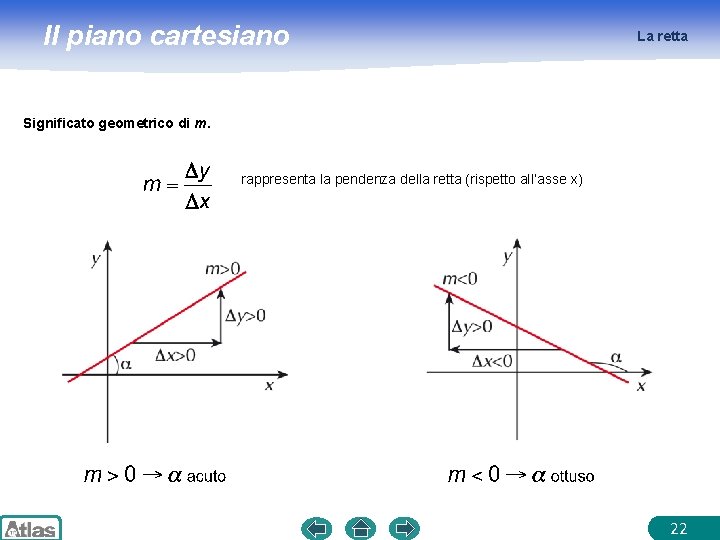
La 'm' di una retta, o coefficiente angolare, è un numero che indica la pendenza della retta stessa. In altre parole, ci dice quanto la retta sale o scende per ogni unità di spostamento orizzontale. Immagina di essere su una montagna: la pendenza del sentiero è analoga al coefficiente angolare di una retta.

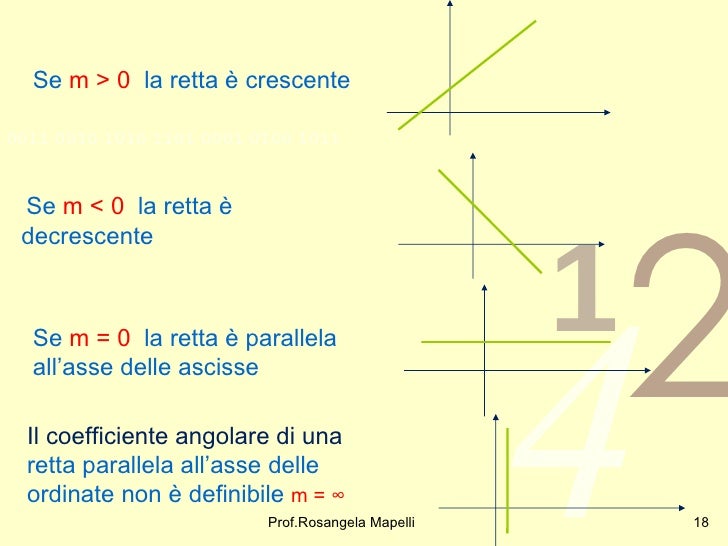
Una 'm' positiva indica che la retta sale da sinistra a destra (come una salita). Più grande è il valore di 'm', più ripida è la salita.

Una 'm' negativa indica che la retta scende da sinistra a destra (come una discesa). Più grande è il valore assoluto di 'm', più ripida è la discesa.

Una 'm' pari a zero indica una retta orizzontale, che non sale né scende.

Una retta verticale ha una 'm' indefinita (o infinita), perché per ogni minimo spostamento verticale non c'è alcuno spostamento orizzontale.

Come calcolare la 'm': diversi approcci

Esistono diversi modi per calcolare il coefficiente angolare di una retta, a seconda delle informazioni che abbiamo a disposizione. Vediamo i più comuni:

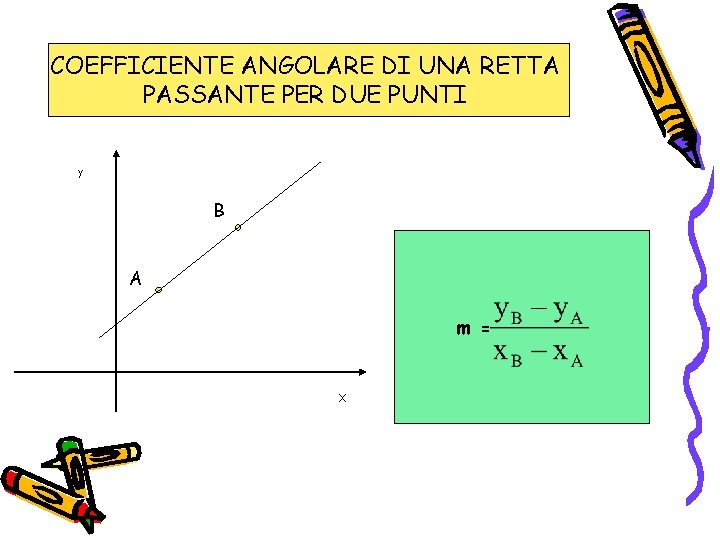
1. Conoscendo due punti sulla retta

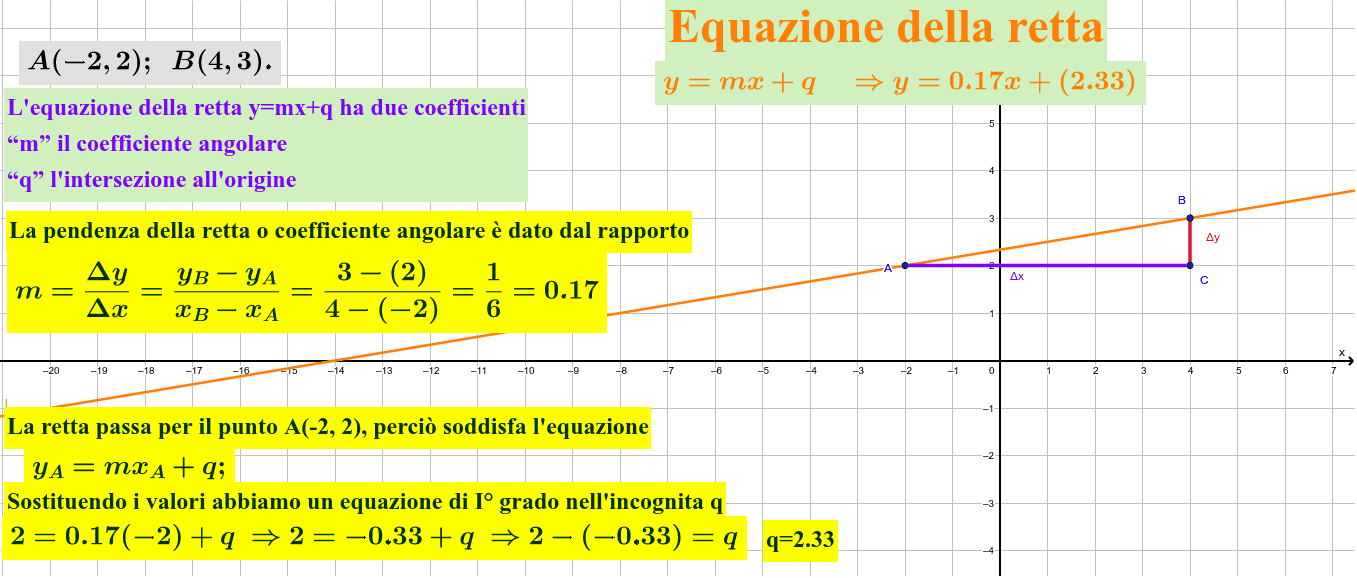
Questo è forse il metodo più utilizzato. Se conosciamo le coordinate di due punti sulla retta, ad esempio (x1, y1) e (x2, y2), possiamo usare la seguente formula:

m = (y2 - y1) / (x2 - x1)

In parole povere, stiamo calcolando la differenza tra le coordinate y (la "variazione verticale") divisa per la differenza tra le coordinate x (la "variazione orizzontale").

Esempio: Supponiamo di avere i punti (1, 2) e (4, 8). Allora:

m = (8 - 2) / (4 - 1) = 6 / 3 = 2

Quindi, la retta ha una pendenza di 2. Questo significa che per ogni unità che ci spostiamo a destra, la retta sale di 2 unità.

2. Conoscendo l'equazione della retta in forma esplicita

L'equazione di una retta in forma esplicita è: y = mx + q

Dove:

• 'y' è la coordinata verticale
• 'x' è la coordinata orizzontale
• 'm' è il coefficiente angolare (quello che stiamo cercando!)
• 'q' è l'intercetta (il punto in cui la retta interseca l'asse y)

In questo caso, trovare la 'm' è semplicissimo: è semplicemente il coefficiente di 'x' nell'equazione.

Esempio: Se l'equazione della retta è y = 3x - 5, allora m = 3.

3. Conoscendo l'angolo che la retta forma con l'asse x

La 'm' è anche uguale alla tangente dell'angolo (θ) che la retta forma con l'asse x:

m = tan(θ)

Questo metodo richiede la conoscenza della trigonometria. Se conosci l'angolo, puoi usare una calcolatrice (o una tabella trigonometrica) per trovare la tangente e quindi la 'm'.

4. A partire dalla forma implicita

Se l'equazione della retta è data in forma implicita, cioè Ax + By + C = 0, possiamo ricavare la forma esplicita per trovare 'm'. Per farlo, isoliamo 'y' da una parte dell'equazione:

By = -Ax - C

y = (-A/B)x - (C/B)

Quindi, in questo caso, m = -A/B

Esempio: Consideriamo l'equazione 2x + 3y - 6 = 0. Qui, A = 2 e B = 3. Quindi, m = -2/3.

Considerazioni importanti e potenziali errori

È importante prestare attenzione ai segni quando si applicano le formule. Un errore di segno può portare a un risultato completamente sbagliato.

Un altro errore comune è invertire le coordinate quando si usa la formula con due punti. Ricorda sempre che la variazione di 'y' va al numeratore e la variazione di 'x' va al denominatore.

Infine, ricordati che una retta verticale ha una 'm' indefinita. Se durante i calcoli ti trovi a dividere per zero, significa che la retta è verticale.

Applicazioni pratiche

Come accennato all'inizio, la 'm' di una retta ha molte applicazioni pratiche:

• Architettura e ingegneria: Calcolare la pendenza di un tetto, di una rampa o di una strada.
• Grafica computerizzata: Definire la traiettoria di oggetti in movimento.
• Statistica: Analizzare la relazione tra due variabili (la 'm' rappresenta la forza e la direzione di questa relazione).
• Finanza: Calcolare il tasso di crescita di un investimento.
• Fisica: Calcolare la velocità di un oggetto (se il grafico rappresenta la posizione in funzione del tempo).

Contro-argomentazioni: alternative alla 'm'

Alcuni potrebbero sostenere che esistono modi più intuitivi per descrivere la pendenza di una retta, come l'angolo di inclinazione rispetto all'orizzontale. Sebbene sia vero che l'angolo fornisce un'informazione simile, la 'm' ha il vantaggio di essere un numero semplice da calcolare e da utilizzare nelle formule. Inoltre, la 'm' può essere positiva o negativa, indicando la direzione della pendenza, mentre l'angolo è sempre positivo.

Un'altra possibile critica è che la 'm' non è definita per le rette verticali. Tuttavia, questo può essere visto come un vantaggio, poiché indica chiaramente che la retta ha una pendenza infinita e quindi richiede un trattamento speciale.

Un approccio "umano" alla matematica

La matematica non è un insieme di regole astratte e impersonali, ma un linguaggio che ci permette di descrivere e comprendere il mondo che ci circonda. Quando affrontiamo un problema di matematica, è utile visualizzare la situazione, cercare di capire il significato dei concetti coinvolti e non limitarsi ad applicare le formule a memoria.

Ad esempio, quando calcoliamo la 'm' di una retta, possiamo immaginare di essere su una collina e di voler calcolare la sua pendenza. Questo ci aiuta a dare un senso ai numeri che stiamo manipolando e a evitare errori.

Ricorda che la matematica è uno strumento potente, ma come ogni strumento, richiede pratica e pazienza per essere padroneggiato. Non scoraggiarti di fronte alle difficoltà, ma persevera e cerca di capire il significato dietro le formule.

Prossimi passi: mettiti alla prova!

Ora che hai imparato come trovare la 'm' di una retta, è il momento di mettere in pratica le tue conoscenze. Ecco alcuni esercizi che puoi provare a risolvere:

• Trova la 'm' della retta che passa per i punti (2, 5) e (6, 13).
• Trova la 'm' della retta di equazione y = -2x + 7.
• Trova la 'm' di una retta che forma un angolo di 45 gradi con l'asse x.
• Una rampa ha un'altezza di 1 metro e una lunghezza di 5 metri. Qual è la sua pendenza (la 'm')?
• Trova la 'm' della retta di equazione 3x - 4y + 8 = 0

Puoi anche cercare online altri esercizi o problemi di geometria analitica. Più ti eserciti, più diventerai bravo a trovare la 'm' di una retta.

Spero che questa guida ti sia stata utile. Se hai ancora domande o dubbi, non esitare a chiedere! Cosa ti spaventa di più quando affronti un problema di geometria analitica?