Come Trovare Le Diagonali Del Rombo Avendo Solo L'area

Calcolare le diagonali di un rombo avendo a disposizione solamente l'area può sembrare un'impresa ardua, ma con la giusta comprensione delle proprietà geometriche del rombo e un pizzico di algebra, è assolutamente fattibile. Questo articolo ti guiderà attraverso i passaggi necessari per raggiungere questo obiettivo, esplorando le formule chiave e fornendo un metodo pratico per risolvere questo tipo di problema.
Il Rombo e le Sue Proprietà Fondamentali
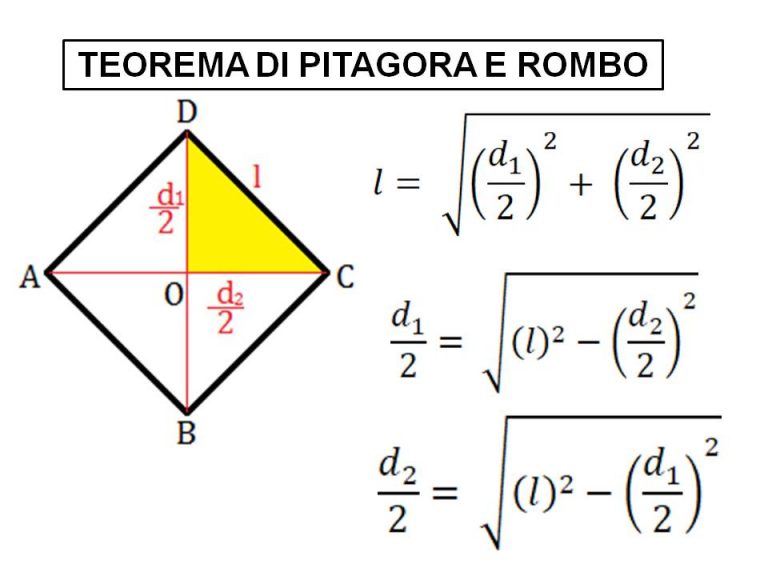
Prima di addentrarci nel calcolo specifico, è fondamentale ripassare le caratteristiche principali del rombo. Un rombo è un parallelogramma con tutti e quattro i lati di uguale lunghezza. Le sue diagonali si intersecano ad angolo retto (90 gradi) e si bisecano a vicenda, dividendosi quindi a metà.
Le Diagonali del Rombo: Pilastri della Geometria
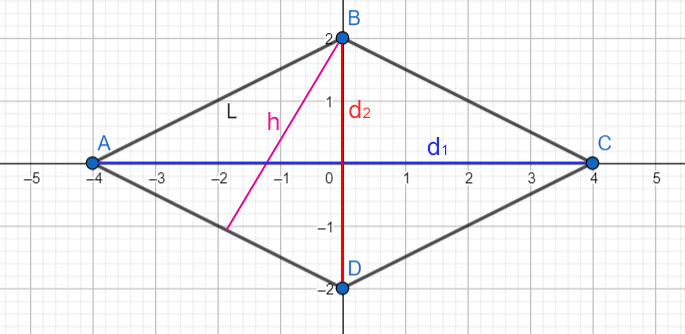
Le diagonali del rombo, spesso indicate con le lettere D (diagonale maggiore) e d (diagonale minore), giocano un ruolo cruciale. Non solo dividono il rombo in quattro triangoli rettangoli congruenti, ma sono anche intimamente legate all'area del rombo stesso. La loro lunghezza determina in gran parte la forma e le dimensioni del rombo.
L'Area del Rombo: La Chiave di Volta
L'area del rombo è data dalla seguente formula:
Area = (D * d) / 2
Dove D rappresenta la lunghezza della diagonale maggiore e d rappresenta la lunghezza della diagonale minore. Questa semplice formula è il punto di partenza per risolvere il nostro problema.
Trovare le Diagonali Conoscendo Solo l'Area: Un Metodo Pratico
Il problema principale risiede nel fatto che abbiamo una sola equazione (quella dell'area) e due incognite (D e d). Pertanto, abbiamo bisogno di ulteriori informazioni o di fare delle assunzioni per risolvere il sistema. Ecco alcuni approcci possibili:
Caso 1: Conoscere il Rapporto tra le Diagonali
Se conosciamo il rapporto tra le diagonali, ad esempio, se sappiamo che la diagonale maggiore è il doppio della diagonale minore (D = 2d), il problema diventa risolvibile. Sostituiamo questa relazione nella formula dell'area:
Area = (2d * d) / 2 = d2
Quindi, d = √Area. Una volta trovata la diagonale minore, possiamo facilmente calcolare la diagonale maggiore usando la relazione D = 2d.
Esempio: Se l'area del rombo è 18 cm2 e sappiamo che la diagonale maggiore è il doppio della diagonale minore, allora:
d = √18 = 3√2 cm
D = 2 * 3√2 = 6√2 cm
Caso 2: Conoscere la Lunghezza di un Lato e un Angolo
Se conosciamo la lunghezza di un lato (l) del rombo e un angolo (α) formato da due lati adiacenti, possiamo usare le funzioni trigonometriche per trovare le diagonali. In particolare:
D = 2 * l * cos(α/2)
d = 2 * l * sin(α/2)
Esempio: Se un lato del rombo misura 5 cm e un angolo è di 60 gradi, allora:
D = 2 * 5 * cos(30°) = 10 * (√3/2) = 5√3 cm
d = 2 * 5 * sin(30°) = 10 * (1/2) = 5 cm
Una volta calcolate le diagonali, possiamo verificare che l'area corrisponda a quella data: (5√3 * 5) / 2 = (25√3)/2 cm2. Calcolando l'area usando un altro metodo: Area = l2 * sin(α) = 52 * sin(60°) = 25 * (√3/2) = (25√3)/2 cm2. I due risultati combaciano.
Caso 3: Conoscere la Somma o la Differenza delle Diagonali
Se conosciamo la somma (S) delle diagonali (D + d = S) o la loro differenza (Diff) (D - d = Diff), possiamo impostare un sistema di equazioni e risolvere per D e d.
Esempio (Somma conosciuta): Supponiamo che l'area del rombo sia 24 cm2 e la somma delle diagonali sia 14 cm. Abbiamo il seguente sistema:
D * d = 48 (Area * 2)
D + d = 14
Da qui, possiamo esprimere D in termini di d (D = 14 - d) e sostituire nella prima equazione:
(14 - d) * d = 48
14d - d2 = 48
d2 - 14d + 48 = 0
Risolvendo l'equazione di secondo grado (usando la formula quadratica), otteniamo due possibili valori per d: 6 e 8. Di conseguenza, i valori corrispondenti per D sono 8 e 6. Quindi, le diagonali sono 6 cm e 8 cm.
Esempio (Differenza conosciuta): Supponiamo che l'area del rombo sia 24 cm2 e la differenza delle diagonali sia 2 cm. Abbiamo il seguente sistema:
D * d = 48 (Area * 2)
D - d = 2
Da qui, possiamo esprimere D in termini di d (D = 2 + d) e sostituire nella prima equazione:
(2 + d) * d = 48
2d + d2 = 48
d2 + 2d - 48 = 0
Risolvendo l'equazione di secondo grado (usando la formula quadratica), otteniamo due possibili valori per d: 6 e -8. Scartiamo il valore negativo dato che la lunghezza non puo' essere negativa. Quindi, il valore corrispondente per D è 8. Quindi, le diagonali sono 6 cm e 8 cm.
Caso 4: L'Impossibilità di una Soluzione Unica
È cruciale comprendere che, conoscendo unicamente l'area, non è possibile determinare univocamente le lunghezze delle diagonali di un rombo. Esistono infiniti rombi con la stessa area, ma con diverse combinazioni di diagonali. Si pensi a un rombo "schiacciato" e a uno più "allungato": entrambi possono avere la stessa area, ma diagonali molto diverse.
Applicazioni Pratiche e Considerazioni Finali
La capacità di calcolare le diagonali di un rombo è utile in diversi contesti pratici. Ad esempio, in architettura e ingegneria, la conoscenza delle dimensioni esatte di una forma romboidale è essenziale per la progettazione e la costruzione di strutture. Nel design grafico, la proporzione delle diagonali può influenzare l'estetica di un logo o di un motivo decorativo.
Inoltre, la comprensione delle relazioni tra l'area e le diagonali di un rombo rafforza la capacità di risolvere problemi geometrici più complessi. Esercitarsi con diversi esempi e scenari aiuta a sviluppare una solida intuizione geometrica.
Conclusione
Sebbene trovare le diagonali di un rombo conoscendo solo l'area richieda informazioni aggiuntive o assunzioni, questo articolo ha fornito un quadro completo delle possibili strategie. Comprendere le proprietà del rombo, la formula dell'area e le relazioni tra le diagonali è fondamentale per affrontare questo tipo di problema. Ricorda, la pratica costante e l'esplorazione di diversi scenari sono la chiave per padroneggiare la geometria!