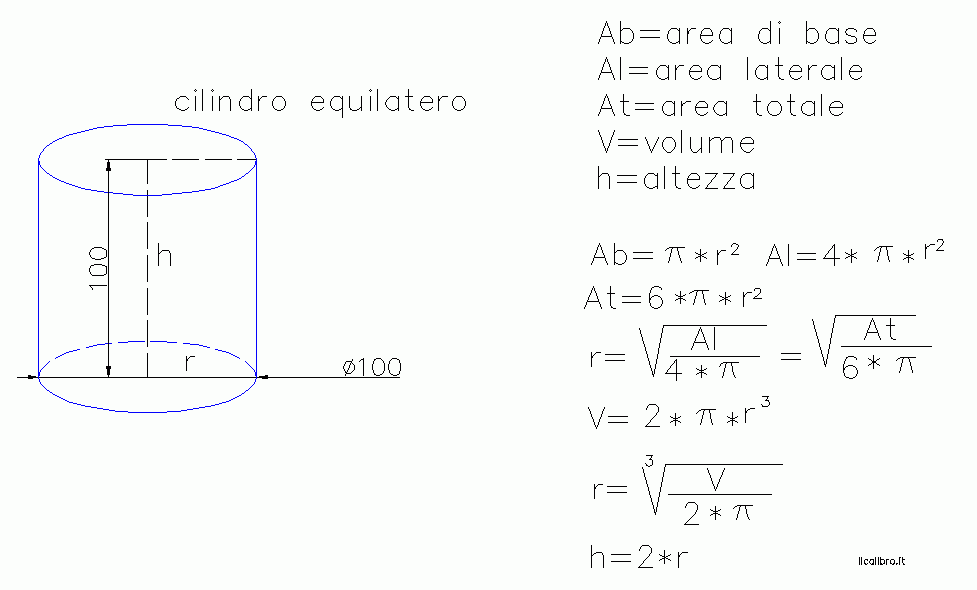Come Trovare L'altezza Di Un Cilindro Senza Il Volume

Ti sei mai trovato di fronte a un problema di geometria, fissando un cilindro disegnato su un foglio, con un unico dato: la sua area di base? E la domanda che ti tormenta è: "Come diavolo trovo l'altezza di questo cilindro se non ho il volume?". Tranquillo, non sei il solo! Molti studenti, e persino professionisti, si imbattono in questa sfida. La buona notizia è che, con un po' di ingegno e le formule giuste, è assolutamente fattibile.

Questo articolo ti guiderà passo dopo passo attraverso i metodi per determinare l'altezza di un cilindro, anche senza conoscere il suo volume. Ti forniremo un approccio chiaro e strutturato, evitando gergo tecnico inutilmente complesso, e rendendo il processo accessibile a tutti.

Capire il Cilindro e le Sue Proprietà

Prima di addentrarci nei calcoli, è fondamentale comprendere le caratteristiche di un cilindro.

Cos'è un cilindro? Un cilindro è una figura geometrica solida con due basi circolari congruenti e parallele, collegate da una superficie curva.

Elementi chiave:

• Base: Un cerchio. Ha un raggio (r) e quindi un'area calcolabile (πr²).
• Altezza (h): La distanza perpendicolare tra le due basi. È quello che stiamo cercando di trovare.
• Superficie Laterale: La superficie curva che collega le due basi.

Ricorda che il volume di un cilindro si calcola con la formula: Volume (V) = πr²h. Ma siccome non abbiamo il volume, dobbiamo esplorare altre vie.

Metodo 1: Conoscendo l'Area della Superficie Totale del Cilindro

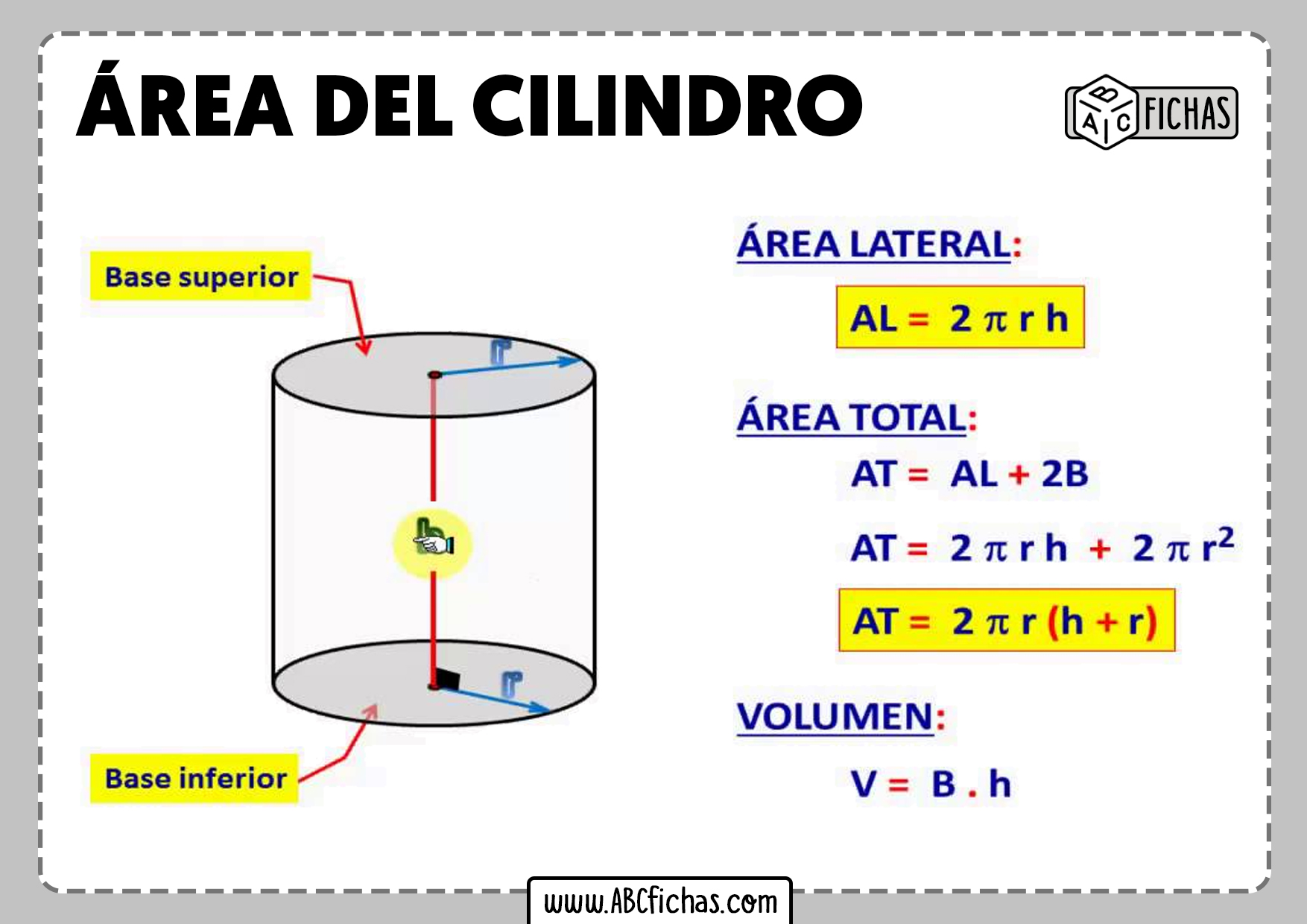
Se ti viene fornita l'area della superficie totale del cilindro (AST), puoi ricavare l'altezza. La formula dell'area della superficie totale è:

AST = 2πr² + 2πrh

Dove:

• AST = Area della superficie totale
• r = Raggio della base
• h = Altezza del cilindro

Passi per calcolare l'altezza:

1. Identifica le informazioni disponibili: Assicurati di conoscere l'area della superficie totale (AST) e il raggio (r) della base. Se ti viene dato il diametro, dividilo per 2 per ottenere il raggio.
2. Sostituisci i valori nella formula: Inserisci i valori di AST e r nella formula AST = 2πr² + 2πrh.
3. Semplifica l'equazione: Esegui le operazioni matematiche per semplificare l'equazione.
4. Isola 'h': L'obiettivo è isolare 'h' da un lato dell'equazione. Ecco come farlo:
   • Sottrai 2πr² da entrambi i lati: AST - 2πr² = 2πrh
   • Dividi entrambi i lati per 2πr: (AST - 2πr²) / (2πr) = h
5. Calcola 'h': Esegui i calcoli finali per trovare il valore dell'altezza (h).

Esempio pratico:

Supponiamo che l'area della superficie totale di un cilindro sia 300π cm² e il raggio della base sia 5 cm. Calcoliamo l'altezza.

1. AST = 300π cm², r = 5 cm
2. 300π = 2π(5)² + 2π(5)h
3. 300π = 50π + 10πh
4. 300π - 50π = 10πh => 250π = 10πh
5. 250π / 10π = h => h = 25 cm

Quindi, l'altezza del cilindro è 25 cm.

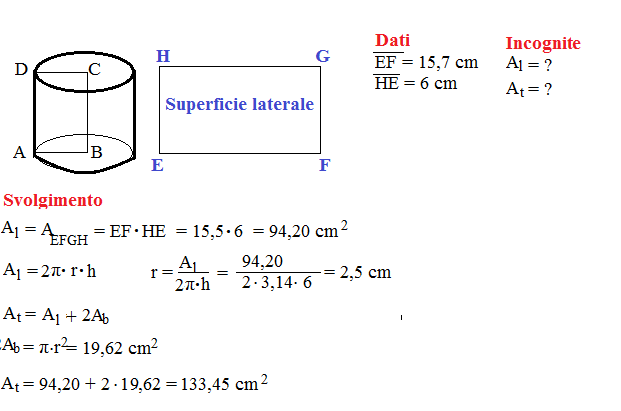
Metodo 2: Conoscendo l'Area della Superficie Laterale del Cilindro

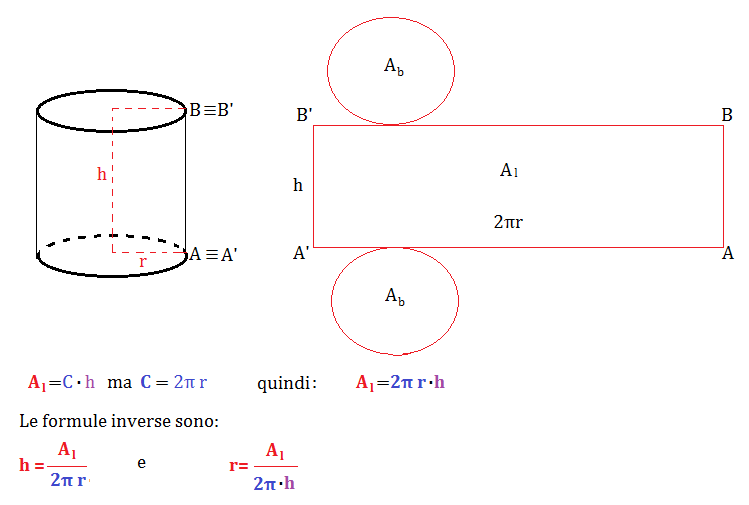
Se invece ti viene fornita l'area della superficie laterale (ASL) del cilindro, il processo è ancora più semplice. La formula dell'area della superficie laterale è:

ASL = 2πrh

Dove:

• ASL = Area della superficie laterale
• r = Raggio della base
• h = Altezza del cilindro

Passi per calcolare l'altezza:

1. Identifica le informazioni disponibili: Assicurati di conoscere l'area della superficie laterale (ASL) e il raggio (r) della base.
2. Sostituisci i valori nella formula: Inserisci i valori di ASL e r nella formula ASL = 2πrh.
3. Isola 'h': Per isolare 'h', dividi entrambi i lati dell'equazione per 2πr:
   • ASL / (2πr) = h
4. Calcola 'h': Esegui il calcolo per trovare il valore dell'altezza (h).

Esempio pratico:

Supponiamo che l'area della superficie laterale di un cilindro sia 120π cm² e il raggio della base sia 4 cm. Calcoliamo l'altezza.

1. ASL = 120π cm², r = 4 cm
2. 120π = 2π(4)h
3. 120π = 8πh
4. 120π / 8π = h => h = 15 cm

Quindi, l'altezza del cilindro è 15 cm.

Metodo 3: Conoscendo la Relazione tra Raggio e Altezza

In alcuni problemi, potrebbe non essere fornita direttamente l'area, ma piuttosto una relazione tra il raggio e l'altezza. Ad esempio, potresti sapere che l'altezza è il doppio del raggio (h = 2r) o che il raggio è la metà dell'altezza (r = h/2). In questi casi, è necessario avere almeno un'altra informazione, come l'area della base.

Esempio:

Supponiamo che l'area della base sia 25π cm² e che l'altezza sia il doppio del raggio (h = 2r).

1. Area della base = πr² = 25π cm²
2. Quindi, r² = 25 => r = 5 cm
3. Sappiamo che h = 2r, quindi h = 2 * 5 = 10 cm

Quindi, l'altezza del cilindro è 10 cm.

Consigli Utili e Precauzioni

• Unità di Misura: Assicurati che tutte le misure siano nella stessa unità di misura prima di eseguire i calcoli. Se hai il raggio in centimetri e l'area in metri quadrati, converti tutto alla stessa unità.
• Precisione: Utilizza un valore preciso di π (pi greco). La calcolatrice di solito fornisce un valore più accurato rispetto a 3.14.
• Ricontrolla: Ricontrolla sempre i tuoi calcoli per evitare errori banali.
• Visualizzazione: Disegna il cilindro e annota le informazioni che hai a disposizione. Questo può aiutarti a visualizzare il problema e a identificare la formula corretta.

Conclusione

Come hai visto, trovare l'altezza di un cilindro senza conoscere il volume è assolutamente possibile! La chiave sta nell'identificare le informazioni disponibili (area della superficie totale, area della superficie laterale, o una relazione tra raggio e altezza) e nell'applicare la formula corretta. Con un po' di pratica e attenzione ai dettagli, sarai in grado di risolvere questo tipo di problema con facilità. Non aver paura di sperimentare e di applicare i concetti appresi a diversi esercizi. La geometria, come la vita, è un problema che si risolve passo dopo passo!