Come Trovare La Diagonale Di Un Rombo Con Il Perimetro

Calcolare la diagonale di un rombo conoscendo il perimetro può sembrare un compito arduo, ma con la giusta comprensione delle proprietà geometriche del rombo e l'applicazione di alcuni principi fondamentali, è possibile risolvere il problema in modo efficace. Questo articolo esplorerà passo dopo passo il processo, fornendo spiegazioni chiare e dettagliate, senza cadere in eccessive semplificazioni.
Comprendere le Proprietà Fondamentali del Rombo
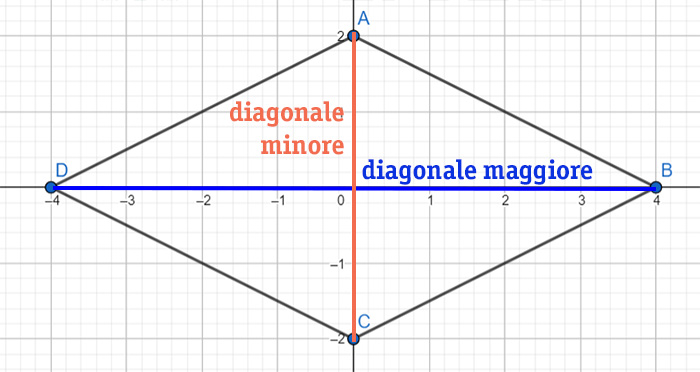
Prima di affrontare il calcolo della diagonale, è cruciale comprendere le caratteristiche distintive del rombo. Un rombo è un quadrilatero con tutti e quattro i lati di uguale lunghezza. Le diagonali di un rombo si intersecano ad angolo retto (90 gradi) e si bisecano a vicenda, il che significa che dividono il rombo in quattro triangoli rettangoli congruenti.
Un'altra proprietà importante è che le diagonali del rombo bisecano gli angoli ai vertici. Questo significa che ogni diagonale divide l'angolo in due angoli uguali. Questa proprietà può essere utile in problemi più complessi, ma per il nostro scopo primario (calcolare la diagonale dal perimetro), la concentrazione è sull'uguaglianza dei lati e l'intersezione perpendicolare delle diagonali.
Il Perimetro come Punto di Partenza
Il perimetro di un rombo è la somma delle lunghezze dei suoi quattro lati. Poiché tutti i lati sono uguali, il perimetro (P) è semplicemente quattro volte la lunghezza di un lato (l):
P = 4 * l
Quindi, se conosciamo il perimetro, possiamo facilmente determinare la lunghezza di un lato dividendo il perimetro per 4:
l = P / 4
Il Teorema di Pitagora: Il Nostro Strumento Chiave
Il Teorema di Pitagora è fondamentale per risolvere questo problema. Ricordiamo che il teorema di Pitagora afferma che in un triangolo rettangolo, il quadrato dell'ipotenusa (il lato opposto all'angolo retto) è uguale alla somma dei quadrati degli altri due lati (i cateti):
a2 + b2 = c2
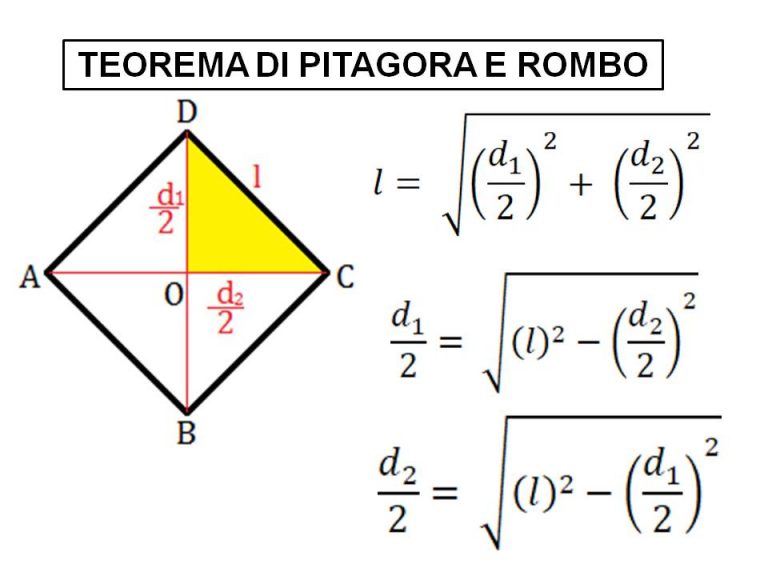
Nel contesto del rombo, possiamo applicare il teorema di Pitagora a uno dei quattro triangoli rettangoli formati dalle diagonali. L'ipotenusa di ciascuno di questi triangoli è un lato del rombo (l), e i cateti sono metà delle lunghezze delle diagonali (d1/2 e d2/2), dove d1 e d2 rappresentano le lunghezze delle due diagonali.
Impostare l'Equazione
Applicando il Teorema di Pitagora, otteniamo la seguente equazione:
(d1/2)2 + (d2/2)2 = l2
Dove 'l' è la lunghezza del lato del rombo, che abbiamo calcolato dal perimetro.
La Sfida: Un'Equazione con Due Incognite
Ora abbiamo un'equazione con due incognite (d1 e d2). Per risolvere un'equazione con due incognite, abbiamo bisogno di un'altra equazione che le metta in relazione. Purtroppo, conoscere solo il perimetro non è sufficiente per determinare univocamente le lunghezze delle due diagonali. Ci sono infinite combinazioni di lunghezze di diagonali che soddisfano l'equazione di Pitagora per un dato lato del rombo.
Esempio: Immaginiamo un rombo con perimetro di 20 cm. Quindi ogni lato misura 5 cm (20/4 = 5). L'equazione diventa:
(d1/2)2 + (d2/2)2 = 52 = 25
o, semplificando:
d12 + d22 = 100
Esistono molteplici soluzioni per d1 e d2 che soddisfano questa equazione. Ad esempio, d1 potrebbe essere 6 cm e d2 8 cm, oppure d1 potrebbe essere 8 cm e d2 6 cm, e così via. Senza ulteriori informazioni, non possiamo determinare una soluzione unica.
Informazioni Aggiuntive Necessarie
Per trovare le diagonali, è necessario disporre di un'ulteriore informazione. Questa informazione potrebbe essere:
- La lunghezza di una delle diagonali.
- La misura di uno degli angoli interni del rombo.
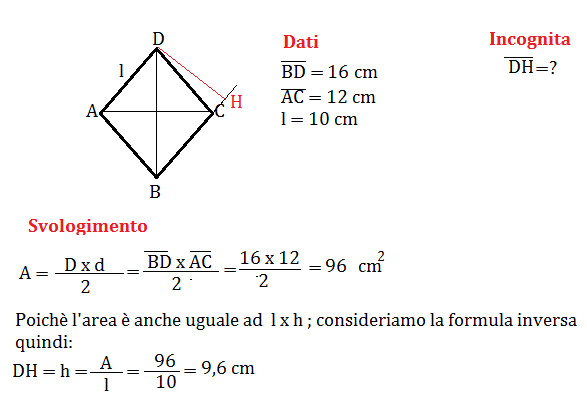
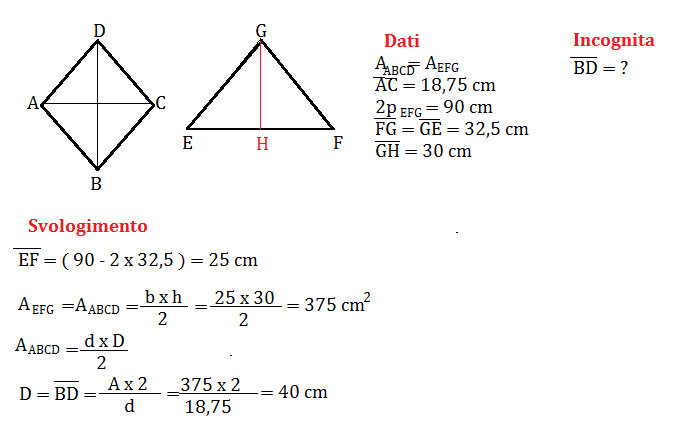
- L'area del rombo.
- Una relazione tra le due diagonali (ad esempio, che una diagonale è il doppio dell'altra).
Esempio con Informazioni Aggiuntive: Conoscendo un Angolo
Supponiamo di sapere che uno degli angoli interni del rombo è di 60 gradi. Poiché le diagonali bisecano gli angoli, uno dei triangoli rettangoli avrà un angolo di 30 gradi (60/2). Possiamo usare la trigonometria per esprimere una diagonale in termini dell'altra.
Se l'angolo è di 60 gradi, allora tan(30°) = (d1/2) / (d2/2) = d1/d2. Sappiamo che tan(30°) = 1/√3. Quindi:
d1/d2 = 1/√3 => d1 = d2/√3
Ora abbiamo una seconda equazione che lega d1 e d2. Possiamo sostituire d1 nell'equazione di Pitagora:
(d2/√3)2 + d22 = 100
d22/3 + d22 = 100
(4/3) * d22 = 100
d22 = 75
d2 = √75 = 5√3 cm
Ora possiamo trovare d1:
d1 = d2/√3 = (5√3)/√3 = 5 cm
In questo caso, siamo stati in grado di trovare le lunghezze delle diagonali perché avevamo informazioni aggiuntive (l'angolo).
Caso Particolare: Il Quadrato
Un caso particolare di rombo è il quadrato. Un quadrato è un rombo con tutti gli angoli retti (90 gradi). In un quadrato, le diagonali sono uguali. Quindi, se sapessimo che il rombo è un quadrato, potremmo semplificare il calcolo. In questo caso, d1 = d2 = d, e l'equazione di Pitagora diventa:
(d/2)2 + (d/2)2 = l2
d2/4 + d2/4 = l2
d2/2 = l2
d2 = 2 * l2
d = √(2 * l2) = l√2
Quindi, se il perimetro è 20 cm e sappiamo che il rombo è un quadrato, allora l = 5 cm e d = 5√2 cm.
Conclusioni
In conclusione, non è possibile calcolare univocamente la diagonale di un rombo conoscendo solamente il perimetro. È necessario disporre di ulteriori informazioni, come la lunghezza di una delle diagonali, la misura di un angolo interno, l'area del rombo o una relazione tra le diagonali. Una volta ottenute queste informazioni aggiuntive, è possibile utilizzare il Teorema di Pitagora e, se necessario, la trigonometria, per risolvere il problema.
Ricorda sempre di analizzare attentamente il problema e identificare tutte le informazioni disponibili prima di iniziare i calcoli. La comprensione delle proprietà geometriche del rombo è essenziale per affrontare questo tipo di problemi in modo efficace.
Per approfondire la tua comprensione, ti incoraggio a risolvere diversi esercizi con diverse informazioni aggiuntive. In questo modo, potrai affinare le tue capacità di problem-solving e acquisire una maggiore familiarità con le proprietà del rombo.