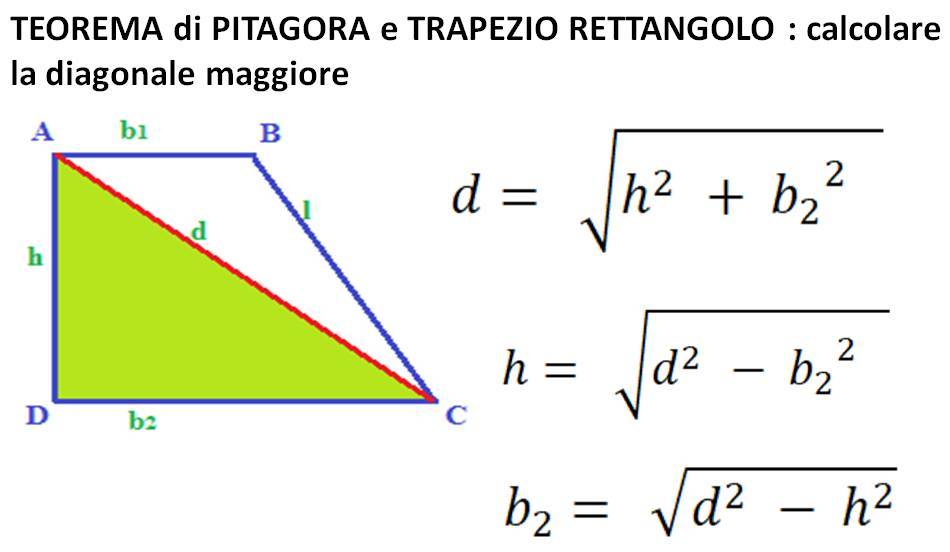
Come Trovare Il Lato Obliquo Di Un Trapezio Rettangolo

Capire la geometria può sembrare a volte un labirinto intricato, soprattutto quando ci si imbatte in figure specifiche come il trapezio rettangolo. Molti studenti e professionisti si trovano a fronteggiare problemi dove è necessario calcolare il lato obliquo, e la frustrazione può essere palpabile. Non preoccuparti, non sei solo! Questo articolo nasce proprio per guidarti passo dopo passo, rendendo questo calcolo accessibile e comprensibile.

Immagina di essere un architetto che deve progettare una facciata con una forma trapezoidale o un falegname che deve tagliare un pezzo di legno con precisione. La capacità di calcolare il lato obliquo di un trapezio rettangolo diventa essenziale per evitare errori costosi e garantire la riuscita del progetto. Non si tratta solo di formule astratte, ma di strumenti concreti che hanno un impatto diretto sulla tua vita professionale e personale.

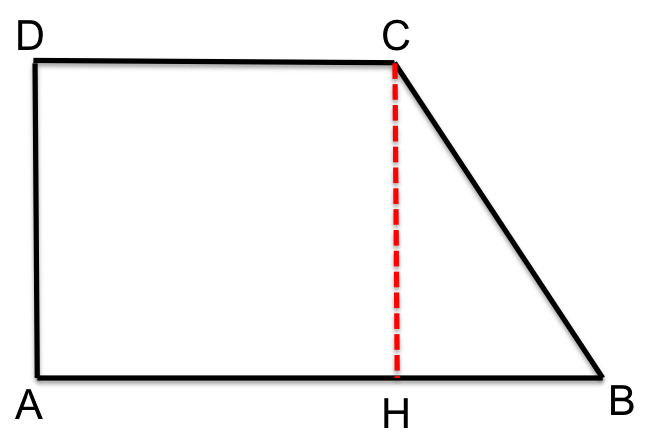
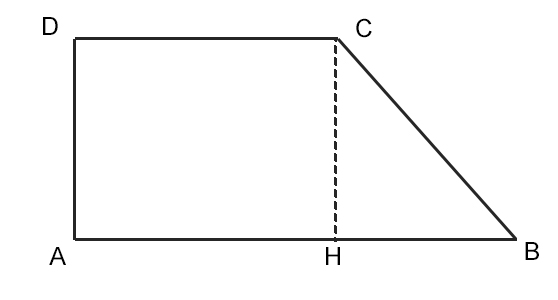
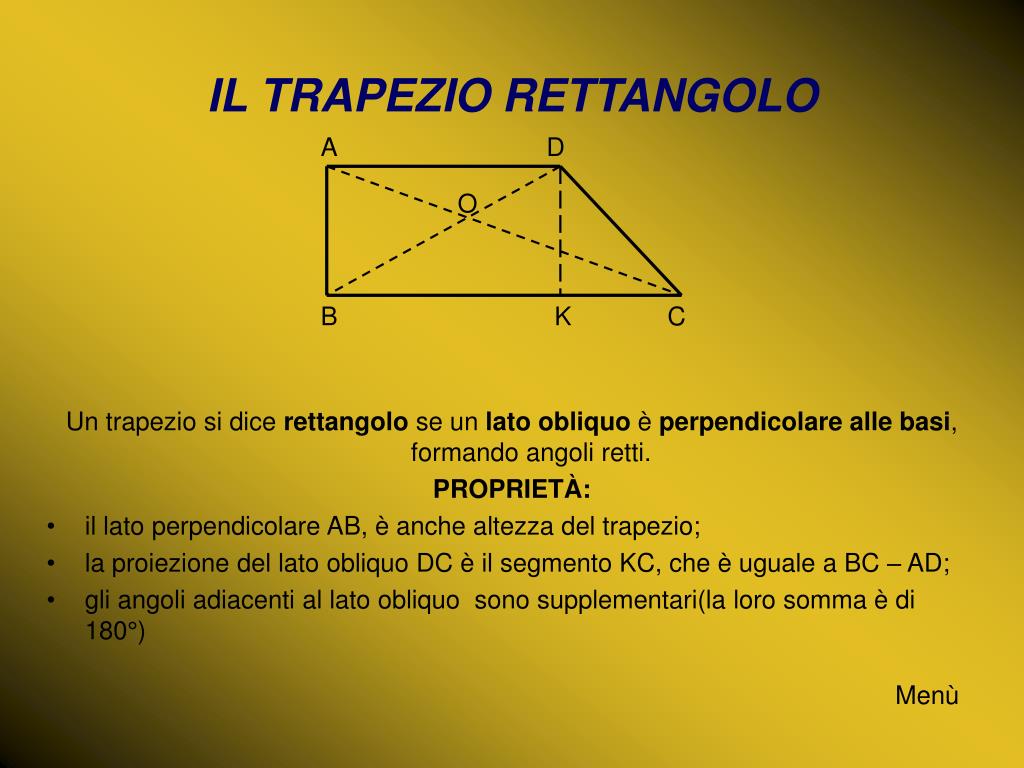
Prima di addentrarci nei metodi di calcolo, è importante definire cosa sia un trapezio rettangolo. Un trapezio rettangolo è un quadrilatero con due lati paralleli (le basi) e due angoli retti. Il lato obliquo è il lato non perpendicolare alle basi.

Metodi per Calcolare il Lato Obliquo

Esistono diversi approcci per calcolare il lato obliquo di un trapezio rettangolo, a seconda delle informazioni che hai a disposizione. Analizziamoli insieme:

1. Utilizzando il Teorema di Pitagora

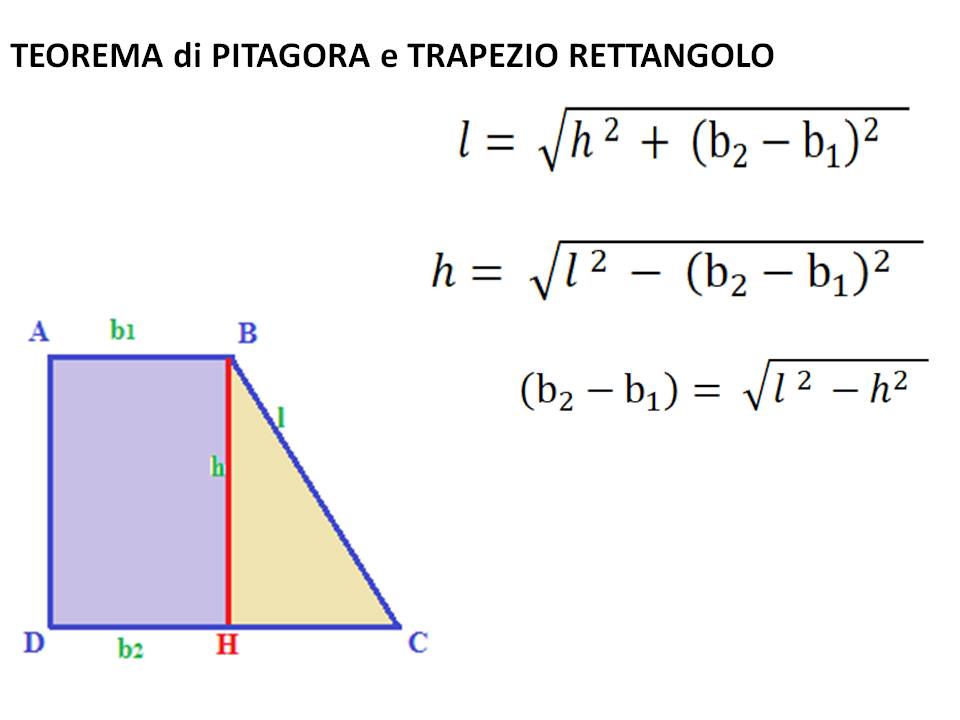
Questo è il metodo più comune e si basa sulla scomposizione del trapezio in un rettangolo e un triangolo rettangolo. Ecco i passaggi:

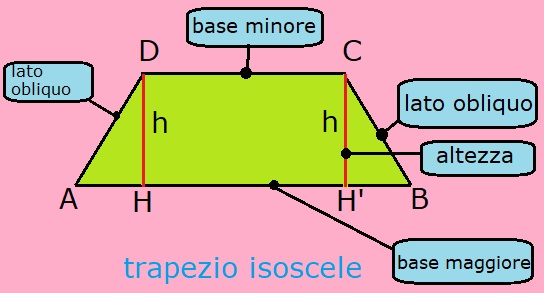
• Identifica le basi: Chiama la base maggiore 'B' e la base minore 'b'.
• Calcola la differenza delle basi: Trova la differenza tra la base maggiore e la base minore: (B - b). Questo valore rappresenta la base del triangolo rettangolo che si forma.
• Individua l'altezza: L'altezza 'h' del trapezio rettangolo è anche un cateto del triangolo rettangolo.
• Applica il Teorema di Pitagora: Il lato obliquo (che chiameremo 'l') è l'ipotenusa del triangolo rettangolo. Quindi, l² = h² + (B - b)².
• Risolvi per 'l': l = √(h² + (B - b)²)

Esempio pratico: Supponiamo che la base maggiore sia 10 cm, la base minore sia 6 cm e l'altezza sia 3 cm. La differenza delle basi è 10 - 6 = 4 cm. Applicando il teorema di Pitagora, l² = 3² + 4² = 9 + 16 = 25. Quindi, l = √25 = 5 cm. Il lato obliquo misura 5 cm.

2. Utilizzando la Trigonometria

Se conosci l'angolo acuto (α) formato dal lato obliquo con la base maggiore, puoi utilizzare le funzioni trigonometriche. Ricorda che il triangolo rettangolo che si forma ha l'angolo α, l'altezza come cateto opposto e la differenza delle basi come cateto adiacente.

• Identifica l'angolo α: Misura l'angolo tra il lato obliquo e la base maggiore.
• Utilizza la funzione seno: sin(α) = h / l, dove 'h' è l'altezza e 'l' è il lato obliquo. Quindi, l = h / sin(α).
• Utilizza la funzione coseno: cos(α) = (B - b) / l, dove (B - b) è la differenza delle basi e 'l' è il lato obliquo. Quindi, l = (B - b) / cos(α).
• Utilizza la funzione tangente: tan(α) = h / (B - b). Questa funzione è utile se devi calcolare l'angolo α conoscendo l'altezza e la differenza delle basi.

Esempio pratico: Supponiamo che l'altezza sia 4 cm e l'angolo α sia 30 gradi. Utilizzando la funzione seno, l = 4 / sin(30°) = 4 / 0.5 = 8 cm. Il lato obliquo misura 8 cm.

3. Utilizzando le Coordinate dei Vertici

Se hai le coordinate dei vertici del trapezio rettangolo, puoi calcolare la lunghezza del lato obliquo utilizzando la formula della distanza tra due punti. Supponiamo che i due vertici del lato obliquo siano (x₁, y₁) e (x₂, y₂).

• Applica la formula della distanza: l = √((x₂ - x₁)² + (y₂ - y₁)²)

Esempio pratico: Supponiamo che i vertici del lato obliquo siano (2, 1) e (6, 4). Applicando la formula della distanza, l = √((6 - 2)² + (4 - 1)²) = √(4² + 3²) = √(16 + 9) = √25 = 5. Il lato obliquo misura 5 unità.

Considerazioni Importanti e Controindicazioni

È fondamentale assicurarsi di utilizzare le unità di misura corrette e consistenti. Se l'altezza è in centimetri, anche le basi devono essere in centimetri per ottenere il lato obliquo in centimetri.

Un errore comune è confondere il lato obliquo con l'altezza. Ricorda sempre che il lato obliquo è l'ipotenusa del triangolo rettangolo che si forma, mentre l'altezza è un cateto.

Alcuni potrebbero sostenere che l'utilizzo di software di geometria dinamica o calcolatrici online rende questi calcoli manuali obsoleti. Tuttavia, la comprensione dei principi fondamentali è cruciale per interpretare correttamente i risultati e per risolvere problemi in contesti in cui non si ha accesso a tali strumenti.

Applicazioni Pratiche

Come accennato all'inizio, la capacità di calcolare il lato obliquo di un trapezio rettangolo ha diverse applicazioni pratiche:

• Architettura e Ingegneria: Progettazione di edifici, ponti e altre strutture.
• Falegnameria e Carpenteria: Taglio preciso di materiali per la costruzione di mobili e altre opere in legno.
• Geometria e Matematica: Risoluzione di problemi geometrici e matematici.
• Grafica e Design: Creazione di immagini e modelli 3D.

Immagina di dover costruire una rampa per disabili. Conoscere le dimensioni della base e l'altezza ti permette di calcolare la lunghezza del piano inclinato (il lato obliquo), garantendo una pendenza adeguata e sicura.

Conclusione

Calcolare il lato obliquo di un trapezio rettangolo non è un'impresa impossibile. Con la giusta comprensione dei concetti geometrici e l'applicazione dei metodi appropriati, puoi affrontare con sicurezza qualsiasi problema. Speriamo che questa guida ti abbia fornito gli strumenti necessari per padroneggiare questo calcolo.

Ricorda, la pratica rende perfetti. Non esitare a esercitarti con diversi esempi e a sperimentare con le varie formule. La geometria può sembrare complessa, ma con pazienza e determinazione, puoi superare qualsiasi ostacolo.

Quale di questi metodi ti sembra il più intuitivo e facile da applicare? Prova a risolvere qualche esercizio e scopri quello che funziona meglio per te! Sei pronto a mettere in pratica ciò che hai imparato?