Come Trovare Il Coefficiente Angolare Di Una Retta

Ti sei mai chiesto come fanno gli architetti a progettare edifici perfettamente allineati? O come i cartografi tracciano rotte precise? La risposta, in parte, risiede nella comprensione del coefficiente angolare, un concetto fondamentale in geometria analitica. Questa guida è pensata per chiunque voglia capire come calcolare il coefficiente angolare di una retta, che tu sia uno studente alle prese con la matematica, un professionista che ha bisogno di rinfrescare le proprie conoscenze o semplicemente una persona curiosa di apprendere qualcosa di nuovo.

Inizieremo definendo cos'è esattamente il coefficiente angolare, per poi esplorare diversi metodi per calcolarlo a partire da informazioni differenti. Che tu abbia a disposizione due punti sulla retta, l'equazione della retta stessa, o l'angolo che la retta forma con l'asse x, imparerai a padroneggiare le tecniche necessarie. Preparati a svelare i segreti delle rette!

Cos'è il Coefficiente Angolare?

Il coefficiente angolare, spesso indicato con la lettera m, è una misura della pendenza di una retta. In termini più semplici, ci dice quanto una retta è ripida e in che direzione si inclina. Una retta con un coefficiente angolare positivo sale verso destra, mentre una retta con un coefficiente angolare negativo scende verso destra. Una retta orizzontale ha un coefficiente angolare pari a zero, e una retta verticale ha un coefficiente angolare indefinito.

Immagina di camminare lungo una strada. Se la strada è pianeggiante, non c'è pendenza, e il coefficiente angolare è zero. Se la strada sale ripida, il coefficiente angolare è alto e positivo. Se la strada scende, il coefficiente angolare è negativo.

Perché è Importante?

Il coefficiente angolare è uno strumento potente che ci permette di:

• Descrivere la direzione e la pendenza di una retta.
• Confrontare la pendenza di due rette diverse.
• Determinare se due rette sono parallele o perpendicolari.
• Costruire equazioni di rette conoscendo alcune informazioni.
• Risolvere problemi di geometria analitica e fisica.

Come Calcolare il Coefficiente Angolare

Esistono diversi modi per calcolare il coefficiente angolare di una retta, a seconda delle informazioni che abbiamo a disposizione. Vediamo i metodi più comuni:

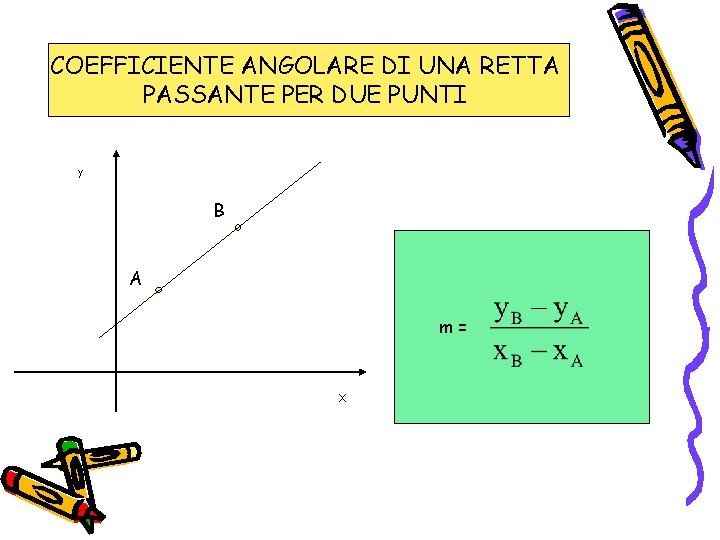
1. Conoscendo Due Punti sulla Retta

Questo è il metodo più fondamentale. Se conosciamo le coordinate di due punti qualsiasi sulla retta, diciamo (x₁, y₁) e (x₂, y₂), possiamo calcolare il coefficiente angolare m usando la seguente formula:

m = (y₂ - y₁) / (x₂ - x₁)

Questa formula rappresenta il rapporto tra la variazione verticale (differenza tra le ordinate) e la variazione orizzontale (differenza tra le ascisse). In altre parole, è la "salita" divisa per la "corsa".

Esempio:

Supponiamo di avere i punti (1, 2) e (3, 6). Calcoliamo il coefficiente angolare:

m = (6 - 2) / (3 - 1) = 4 / 2 = 2

Quindi, il coefficiente angolare della retta che passa per i punti (1, 2) e (3, 6) è 2. Questo significa che per ogni unità che ci spostiamo verso destra sull'asse x, la retta sale di 2 unità sull'asse y.

2. Conoscendo l'Equazione della Retta in Forma Esplicita

L'equazione di una retta in forma esplicita è:

y = mx + q

Dove:

• y rappresenta l'ordinata di un punto qualsiasi sulla retta.
• x rappresenta l'ascissa di un punto qualsiasi sulla retta.
• m è il coefficiente angolare (quello che stiamo cercando!).
• q è l'intercetta, ovvero il punto in cui la retta interseca l'asse y (l'ordinata all'origine).

In questa forma, il coefficiente angolare è semplicemente il numero che moltiplica la variabile x.

Esempio:

Consideriamo l'equazione della retta y = 3x - 5. In questo caso, il coefficiente angolare è 3, e l'intercetta è -5.

3. Conoscendo l'Equazione della Retta in Forma Implicita

L'equazione di una retta in forma implicita è:

Ax + By + C = 0

Dove A, B e C sono costanti. Per trovare il coefficiente angolare da questa forma, dobbiamo prima trasformare l'equazione nella forma esplicita (y = mx + q). Possiamo farlo risolvendo l'equazione per y:

By = -Ax - C

y = (-A/B)x - (C/B)

Ora possiamo vedere che il coefficiente angolare m è uguale a -A/B.

Esempio:

Consideriamo l'equazione della retta 2x + 3y - 6 = 0. Per trovare il coefficiente angolare, seguiamo questi passaggi:

3y = -2x + 6

y = (-2/3)x + 2

Quindi, il coefficiente angolare è -2/3.

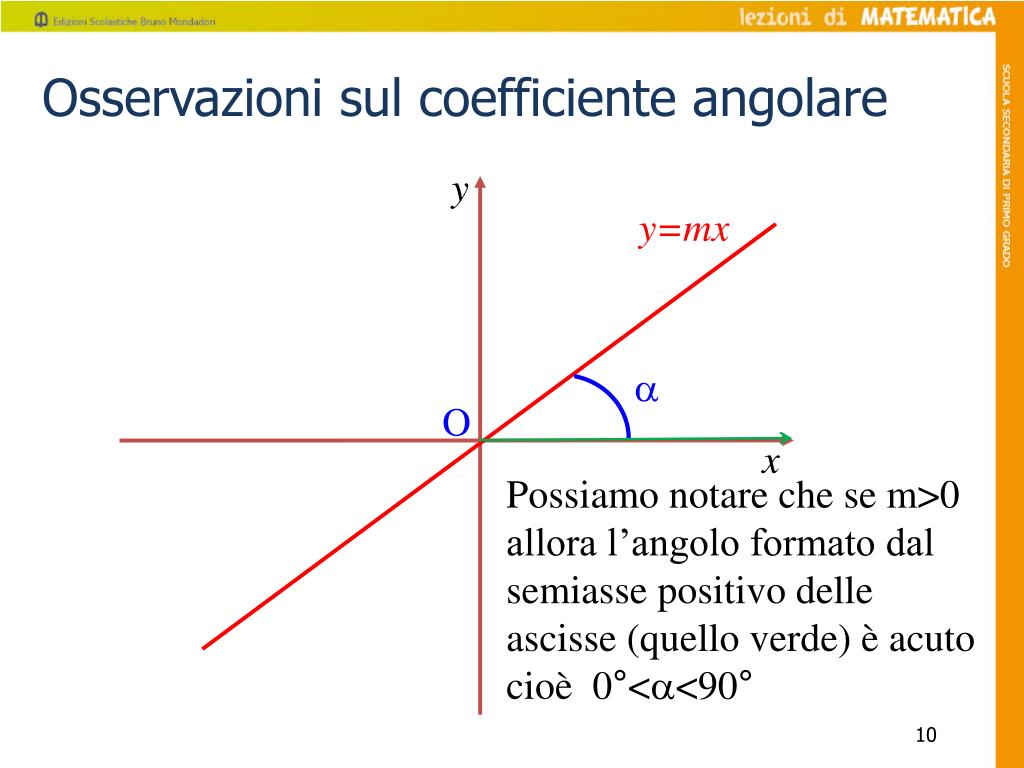
4. Conoscendo l'Angolo che la Retta Forma con l'Asse x

Il coefficiente angolare è legato all'angolo che la retta forma con l'asse x (solitamente indicato con la lettera greca θ, theta) tramite la funzione tangente:

m = tan(θ)

La tangente di un angolo è il rapporto tra il seno e il coseno dell'angolo. Se conosci l'angolo θ in gradi o radianti, puoi usare una calcolatrice per trovare la sua tangente e quindi determinare il coefficiente angolare.

Esempio:

Se una retta forma un angolo di 45 gradi con l'asse x, il suo coefficiente angolare è:

m = tan(45°) = 1

Questo significa che la retta sale di una unità sull'asse y per ogni unità che ci spostiamo verso destra sull'asse x.

Rette Parallele e Perpendicolari

Il coefficiente angolare ci permette anche di determinare se due rette sono parallele o perpendicolari.

• Rette Parallele: Due rette sono parallele se e solo se hanno lo stesso coefficiente angolare. In altre parole, se m₁ = m₂, allora le rette sono parallele.
• Rette Perpendicolari: Due rette sono perpendicolari se e solo se il prodotto dei loro coefficienti angolari è -1. In altre parole, se m₁ * m₂ = -1, allora le rette sono perpendicolari. Equivalentemente, il coefficiente angolare di una retta è l'inverso negativo del coefficiente angolare dell'altra retta. Ad esempio, se m₁ = 2, allora m₂ = -1/2.

Esercizi Pratici

Per consolidare la tua comprensione, prova a risolvere i seguenti esercizi:

1. Trova il coefficiente angolare della retta che passa per i punti (2, 5) e (4, 9).
2. Trova il coefficiente angolare della retta con equazione y = -2x + 7.
3. Trova il coefficiente angolare della retta con equazione 5x - 2y + 1 = 0.
4. Trova il coefficiente angolare di una retta che forma un angolo di 60 gradi con l'asse x.
5. Sono le rette y = 4x + 1 e y = 4x - 3 parallele?
6. Sono le rette y = 2x + 5 e y = -1/2x - 1 perpendicolari?

Conclusione

Speriamo che questa guida ti abbia fornito una comprensione chiara e completa di come trovare il coefficiente angolare di una retta. Ricorda che il coefficiente angolare è uno strumento fondamentale in matematica e in molte altre discipline, e padroneggiarlo ti aprirà le porte a una comprensione più profonda del mondo che ci circonda. Non esitare a esercitarti con diversi esempi e a consultare altre risorse se hai bisogno di ulteriore aiuto. Buono studio!