Come Trovare Il Coefficiente Angolare Con Un Punto

Ti sei mai trovato di fronte a una retta e ti sei chiesto quanto è ripida? O, più precisamente, come quantificare matematicamente la sua pendenza? La risposta è il coefficiente angolare, un concetto fondamentale in geometria analitica che descrive l'inclinazione di una retta rispetto all'asse delle ascisse. Questo articolo è pensato per chiunque voglia capire come trovare il coefficiente angolare, anche senza una preparazione matematica avanzata. Che tu sia uno studente alle prese con i compiti, un professionista che ha bisogno di rinfrescare le proprie conoscenze, o semplicemente curioso di matematica, questa guida ti fornirà gli strumenti necessari.

Cos'è il Coefficiente Angolare?

Il coefficiente angolare, spesso indicato con la lettera m, è un numero che rappresenta la pendenza di una retta. In termini semplici, indica quanto la retta sale o scende per ogni unità di spostamento orizzontale. Un coefficiente angolare positivo indica una retta crescente (che sale da sinistra a destra), mentre un coefficiente angolare negativo indica una retta decrescente (che scende da sinistra a destra). Un coefficiente angolare pari a zero indica una retta orizzontale.

Perché è importante?

Il coefficiente angolare è cruciale per diverse ragioni:

Descrizione geometrica: Permette di descrivere in modo preciso e univoco l'inclinazione di una retta.
Equazioni delle rette: È un elemento fondamentale nell'equazione di una retta, sia in forma esplicita (y = mx + q) che implicita.
Applicazioni pratiche: Trova applicazioni in fisica (ad esempio, nel calcolo della velocità), ingegneria (ad esempio, nella progettazione di rampe) ed economia (ad esempio, nell'analisi di grafici di domanda e offerta).

Come Trovare il Coefficiente Angolare: Diversi Scenari

Esistono diversi modi per calcolare il coefficiente angolare, a seconda delle informazioni che abbiamo a disposizione. Vediamo i casi più comuni:

1. Conoscendo Due Punti sulla Retta

Questo è il metodo più comune. Se conosciamo le coordinate di due punti sulla retta, diciamo (x₁, y₁) e (x₂, y₂), possiamo calcolare il coefficiente angolare usando la seguente formula:

m = (y₂ - y₁) / (x₂ - x₁)

In parole povere, il coefficiente angolare è la variazione di y (la differenza tra le coordinate y dei due punti) divisa per la variazione di x (la differenza tra le coordinate x dei due punti). È importante mantenere lo stesso ordine quando si calcolano le differenze; ovvero, se si inizia con y₂, si deve iniziare anche con x₂ al denominatore.

Esempio: Supponiamo di avere i punti A(1, 2) e B(3, 6). Calcoliamo il coefficiente angolare:

m = (6 - 2) / (3 - 1) = 4 / 2 = 2

Quindi, il coefficiente angolare della retta che passa per i punti A e B è 2. Questo significa che per ogni unità che ci spostiamo verso destra sull'asse delle x, la retta sale di 2 unità sull'asse delle y.

2. Conoscendo l'Equazione della Retta in Forma Esplicita

L'equazione di una retta in forma esplicita è: y = mx + q

Dove:

y è la coordinata verticale.
x è la coordinata orizzontale.
m è il coefficiente angolare (che stiamo cercando!).
q è l'ordinata all'origine (il punto in cui la retta interseca l'asse delle y).

Se l'equazione della retta è già in questa forma, trovare il coefficiente angolare è semplicissimo: è il numero che moltiplica la x!

Esempio: Consideriamo l'equazione y = 3x + 5. In questo caso, il coefficiente angolare è m = 3.

3. Conoscendo l'Equazione della Retta in Forma Implicita

L'equazione di una retta in forma implicita è: ax + by + c = 0

Dove a, b, e c sono costanti. Per trovare il coefficiente angolare in questo caso, dobbiamo prima trasformare l'equazione nella forma esplicita. Isoliamo y:

by = -ax - c

y = (-a/b)x - (c/b)

Ora che l'equazione è in forma esplicita, possiamo identificare il coefficiente angolare come il coefficiente di x:

m = -a/b

Esempio: Consideriamo l'equazione 2x + 3y - 6 = 0. Allora a = 2 e b = 3. Il coefficiente angolare è:

m = -2/3

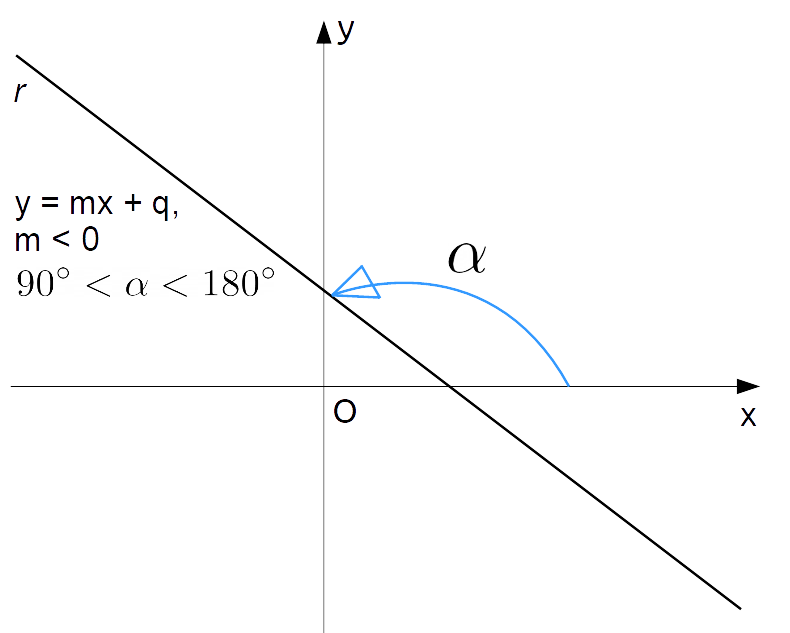
4. Conoscendo l'Angolo che la Retta Forma con l'Asse delle Ascisse

Il coefficiente angolare è anche legato all'angolo che la retta forma con l'asse delle ascisse (l'asse x). Se conosciamo questo angolo, chiamiamolo θ (theta), possiamo calcolare il coefficiente angolare usando la tangente dell'angolo:

m = tan(θ)

Esempio: Se una retta forma un angolo di 45 gradi con l'asse delle ascisse, il suo coefficiente angolare è:

m = tan(45°) = 1

Questo perché la tangente di 45 gradi è uguale a 1.

Esercizi Pratici

Per consolidare la tua comprensione, proviamo a risolvere alcuni esercizi insieme:

Trova il coefficiente angolare della retta che passa per i punti (2, 5) e (4, 9).
Trova il coefficiente angolare della retta con equazione y = -2x + 7.
Trova il coefficiente angolare della retta con equazione x - 4y + 8 = 0.
Trova il coefficiente angolare della retta che forma un angolo di 60 gradi con l'asse delle ascisse.

Soluzioni:

m = (9 - 5) / (4 - 2) = 4 / 2 = 2
m = -2
m = 1/4 (Ricorda di isolare y prima di identificare il coefficiente angolare)
m = tan(60°) = √3 (radice quadrata di 3)

Errori Comuni da Evitare

Ecco alcuni errori comuni che è bene evitare quando si calcola il coefficiente angolare:

Inversione delle coordinate: Assicurati di calcolare la variazione di y divisa per la variazione di x, e non il contrario.
Inversione dell'ordine dei punti: Quando usi la formula con due punti, assicurati di mantenere lo stesso ordine (y₂ - y₁ e x₂ - x₁).
Confusione tra forma implicita ed esplicita: Assicurati che l'equazione sia in forma esplicita (y = mx + q) prima di identificare il coefficiente angolare.
Dimenticare il segno negativo nella forma implicita: Quando usi la formula m = -a/b per la forma implicita, non dimenticare il segno meno.

Conclusione

Speriamo che questa guida ti abbia fornito una chiara comprensione di come trovare il coefficiente angolare in diverse situazioni. Ricorda, la pratica rende perfetti! Più esercizi risolverai, più diventerai sicuro nel calcolare il coefficiente angolare. Questo concetto è un mattone fondamentale per comprendere concetti più avanzati di geometria analitica e calcolo. Quindi, continua a esercitarti e non aver paura di fare domande. Buono studio!