Come Sono I Lati Del Rombo

Avete mai ammirato un aquilone che solca il cielo, o la trama intricata di un motivo geometrico? Spesso, al centro di queste figure, si nasconde un affascinante quadrilatero: il rombo. Questo articolo è pensato per chiunque, dagli studenti alle persone semplicemente curiose, desideri esplorare a fondo le proprietà e le caratteristiche dei lati del rombo. Cercheremo di rispondere in modo chiaro e completo alla domanda: come sono i lati del rombo?

Cos'è un Rombo? Una Definizione Chiara

Prima di addentrarci nei dettagli dei suoi lati, definiamo cos'è esattamente un rombo. Un rombo è un quadrilatero (una figura geometrica con quattro lati) che possiede due proprietà fondamentali:

• Tutti i suoi quattro lati sono congruenti, ovvero hanno la stessa lunghezza.
• Le sue diagonali si bisecano ad angolo retto (90 gradi).

Questa definizione è cruciale per comprendere le caratteristiche che distinguono il rombo da altri quadrilateri come il quadrato, il rettangolo o il parallelogramma. Il quadrato, ad esempio, è un caso particolare di rombo in cui anche gli angoli sono retti.

La Caratteristica Fondamentale: Lati Congruenti

La proprietà più importante e distintiva del rombo è che tutti i suoi lati sono uguali. Questo significa che se misuriamo la lunghezza di un lato, tutti gli altri lati avranno esattamente la stessa misura. Questa congruenza dei lati è la base per molte altre proprietà e calcoli che riguardano il rombo.

Immaginate di dover costruire una cornice a forma di rombo. Sapere che i lati sono uguali semplificherebbe enormemente il lavoro, perché dovreste solo tagliare quattro pezzi della stessa lunghezza e unirli seguendo gli angoli appropriati.

Come Verificare la Congruenza dei Lati

Esistono diversi modi per verificare se un quadrilatero è effettivamente un rombo, concentrandosi sulla congruenza dei lati:

• Misurazione Diretta: Il metodo più semplice è misurare direttamente la lunghezza di ciascun lato. Se tutte le misurazioni sono identiche, allora il quadrilatero soddisfa la condizione per essere un rombo.
• Coordinate nel Piano Cartesiano: Se i vertici del quadrilatero sono definiti da coordinate in un piano cartesiano, possiamo utilizzare la formula della distanza tra due punti per calcolare la lunghezza di ciascun lato. Anche in questo caso, se le lunghezze sono uguali, abbiamo un rombo.
• Utilizzo di Strumenti di Geometria: Software di geometria dinamica (come GeoGebra) permettono di disegnare quadrilateri e verificare automaticamente se i lati sono congruenti.

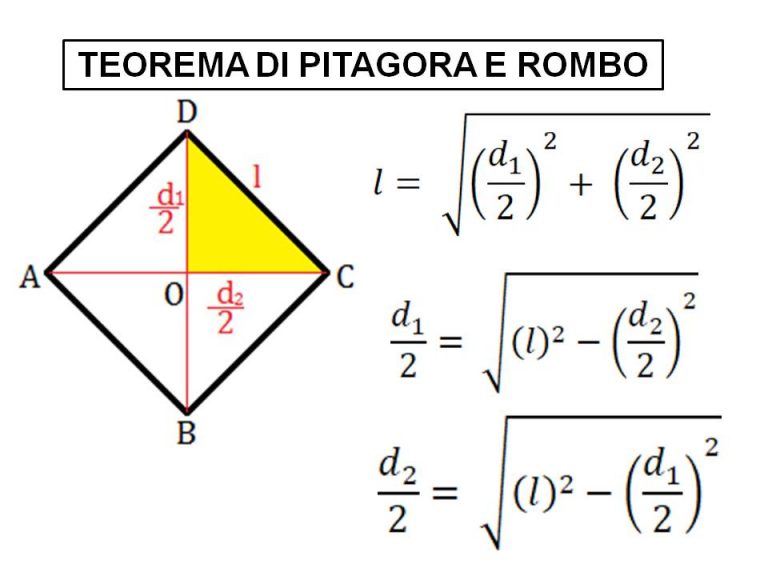
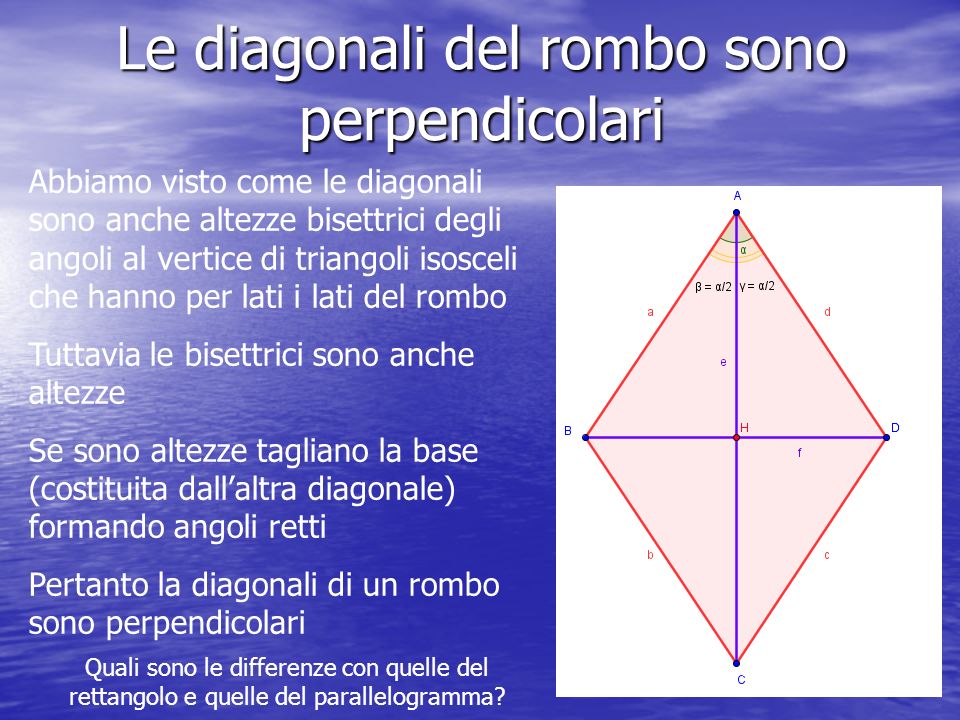
Le Diagonali del Rombo e la Loro Relazione con i Lati

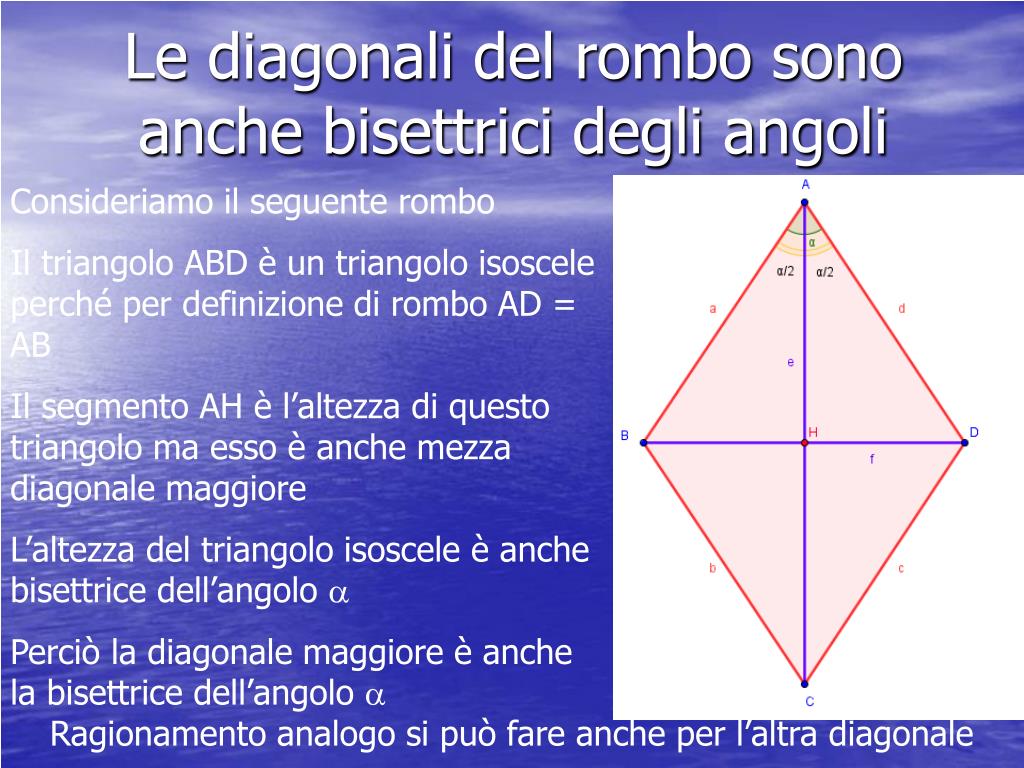
Le diagonali del rombo giocano un ruolo fondamentale nella sua geometria e sono strettamente legate alla lunghezza dei lati. Ricordiamo che le diagonali del rombo si bisecano ad angolo retto.

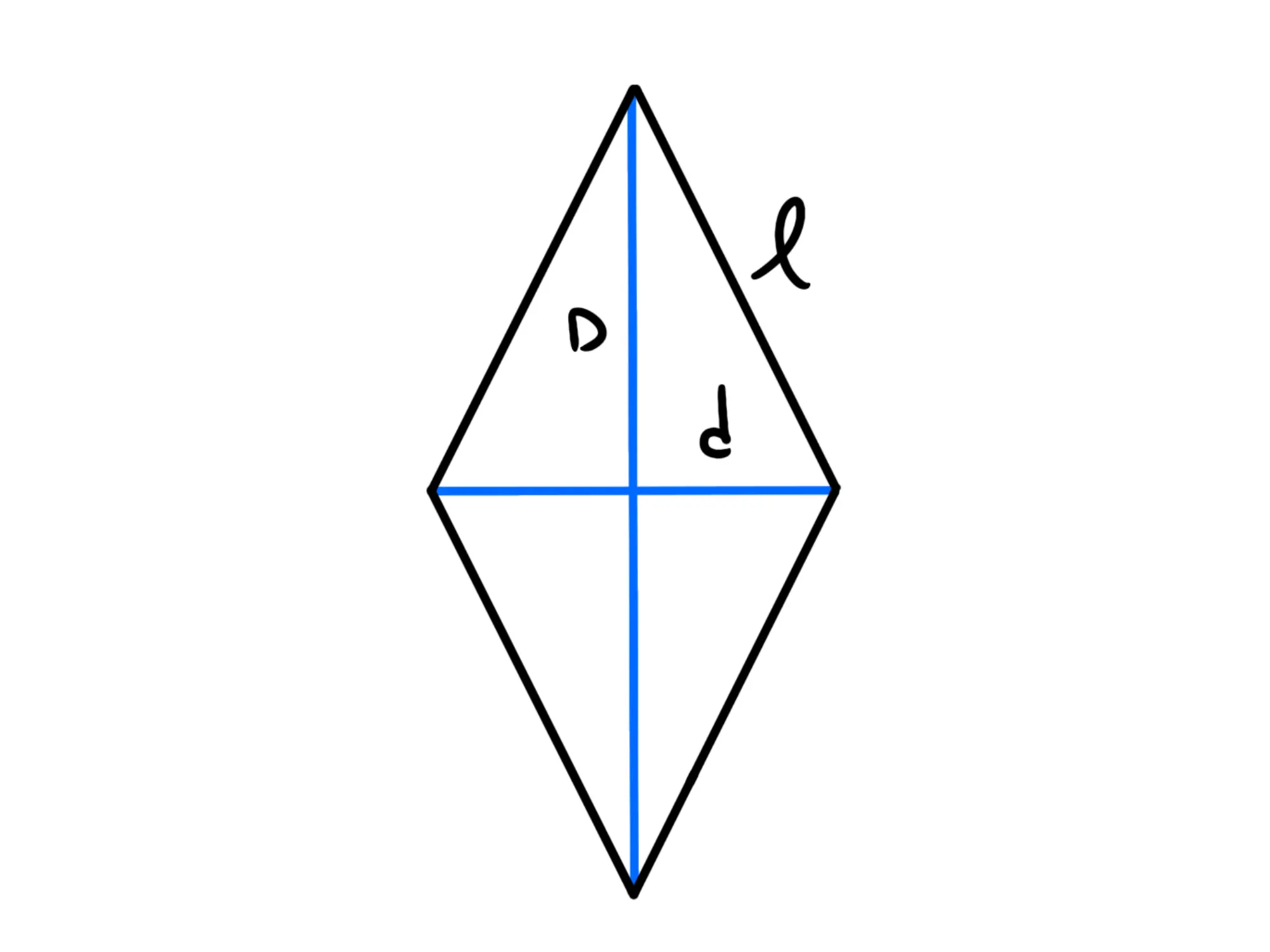
Questa proprietà crea quattro triangoli rettangoli congruenti all'interno del rombo. L'ipotenusa di ciascuno di questi triangoli rettangoli è un lato del rombo, e i cateti sono metà delle diagonali.

Il Teorema di Pitagora in Azione

Possiamo sfruttare il teorema di Pitagora per mettere in relazione la lunghezza dei lati del rombo (l) con le lunghezze delle sue diagonali (d1 e d2):

l² = (d1/2)² + (d2/2)²

Questa formula ci permette di calcolare la lunghezza di un lato del rombo se conosciamo la lunghezza delle diagonali, o viceversa.

Esempio Pratico: Immaginiamo un rombo con diagonali lunghe 6 cm e 8 cm. Per trovare la lunghezza del lato, applichiamo la formula:

l² = (6/2)² + (8/2)² = 3² + 4² = 9 + 16 = 25

l = √25 = 5 cm

Quindi, la lunghezza di ciascun lato del rombo è di 5 cm.

Angoli del Rombo: Un'Altra Caratteristica Importante

Sebbene il focus principale di questo articolo siano i lati del rombo, è importante considerare anche gli angoli, perché sono interconnessi. A differenza del quadrato, gli angoli del rombo non sono necessariamente retti. Le seguenti proprietà sono fondamentali:

• Gli angoli opposti sono congruenti.
• Gli angoli adiacenti sono supplementari (la loro somma è 180 gradi).
• Le diagonali bisecano gli angoli del rombo. Questo significa che ogni diagonale divide l'angolo in due angoli uguali.

La relazione tra i lati e gli angoli è fondamentale per calcolare l'area del rombo, come vedremo nel prossimo paragrafo.

Come Calcolare l'Area del Rombo

Esistono diversi modi per calcolare l'area del rombo, e alcuni di essi dipendono direttamente dalla lunghezza dei suoi lati:

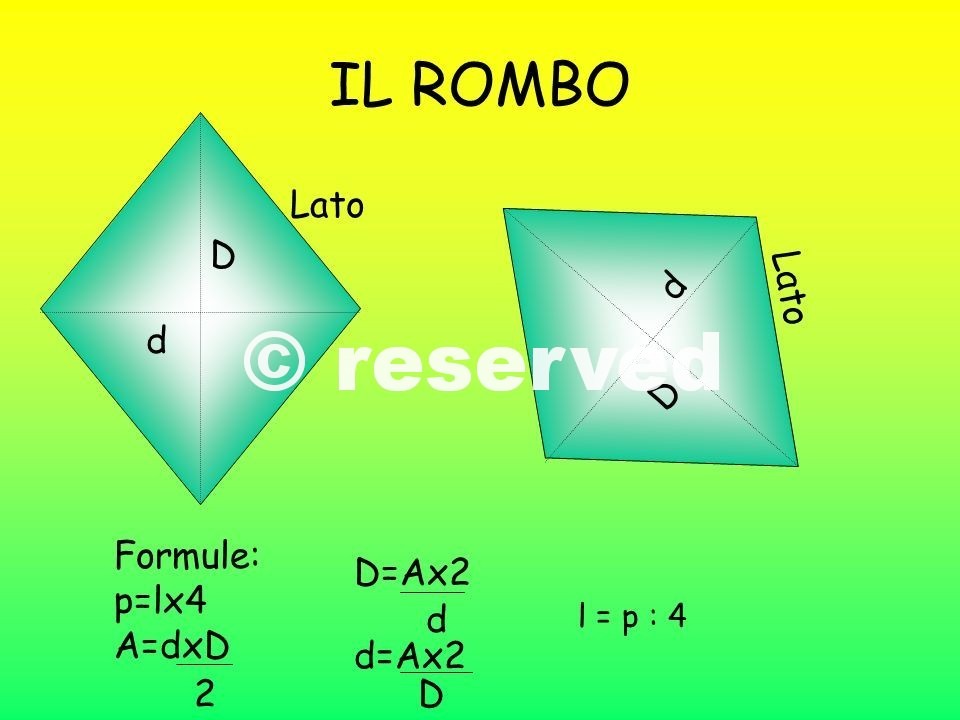
• Utilizzando le Diagonali: L'area del rombo è uguale alla metà del prodotto delle sue diagonali:

  Area = (d1 * d2) / 2

• Utilizzando il Lato e l'Altezza: L'area del rombo può anche essere calcolata moltiplicando la lunghezza di un lato per l'altezza relativa a quel lato (la distanza perpendicolare tra quel lato e il lato opposto):

  Area = lato * altezza

• Utilizzando la Trigonometria: Se conosciamo la lunghezza di un lato (l) e un angolo (α), possiamo usare la seguente formula:

  Area = l² * sin(α)

Come si può notare, la conoscenza della lunghezza dei lati è essenziale per calcolare l'area del rombo utilizzando diversi metodi. La scelta del metodo più appropriato dipende dalle informazioni che abbiamo a disposizione.

Rombo vs. Altri Quadrilateri: Cosa lo Rende Unico?

È fondamentale distinguere il rombo da altri quadrilateri per comprenderne appieno le proprietà. Confrontiamolo con alcune figure geometriche simili:

• Quadrato: Un quadrato è un rombo con quattro angoli retti. In altre parole, è un rombo "perfetto" con tutte le caratteristiche "ottimizzate".
• Rettangolo: Un rettangolo ha quattro angoli retti, ma i suoi lati non sono necessariamente tutti uguali.
• Parallelogramma: Un parallelogramma ha i lati opposti paralleli e congruenti, ma i suoi lati non sono necessariamente tutti uguali e gli angoli non sono necessariamente retti. Un rombo è un parallelogramma speciale con tutti i lati uguali.
• Trapezio: Un trapezio ha solo una coppia di lati paralleli.

La congruenza dei lati è la caratteristica distintiva che separa il rombo dai parallelogrammi e dai trapezi. Il quadrato, pur condividendo la congruenza dei lati, si distingue per avere tutti gli angoli retti.

Applicazioni Pratiche del Rombo

Il rombo non è solo una figura geometrica astratta. Trova applicazioni in diversi campi, dalla vita quotidiana all'ingegneria e all'arte:

• Design e Architettura: Motivi romboidali sono spesso utilizzati in pavimentazioni, tessuti, decorazioni e facciate di edifici. La loro forma geometrica aggiunge un tocco di eleganza e dinamicità.
• Ingegneria: Strutture a forma di rombo possono essere utilizzate per la loro resistenza e stabilità, ad esempio in ponti o tralicci.
• Gioielleria: La forma del rombo è utilizzata per tagliare gemme preziose, esaltandone la brillantezza.
• Aquiloni: Come menzionato all'inizio, molti aquiloni hanno una forma romboidale, sfruttando le proprietà aerodinamiche di questa figura.

La prossima volta che vedrete una griglia di metallo, un motivo decorativo o un diamante tagliato, ricordatevi del rombo e delle sue affascinanti proprietà geometriche.

In Conclusione: I Lati del Rombo in Sintesi

In sintesi, la caratteristica principale dei lati del rombo è la loro congruenza. Tutti e quattro i lati di un rombo hanno la stessa lunghezza. Questa proprietà, combinata con la bisettrice perpendicolare delle diagonali, rende il rombo una figura geometrica unica e interessante. Abbiamo esplorato come verificare la congruenza dei lati, come utilizzare il teorema di Pitagora per collegare i lati alle diagonali, e come calcolare l'area del rombo. Speriamo che questo articolo vi abbia fornito una comprensione completa dei lati del rombo e delle loro proprietà. La geometria è ovunque intorno a noi, e conoscere le forme che ci circondano arricchisce la nostra percezione del mondo!