Come Si Trova La Base Del Parallelogramma

Il parallelogramma, una figura geometrica fondamentale, si presenta in diverse forme nella nostra vita quotidiana, dall'architettura al design. Comprendere come calcolare la sua base è essenziale per una varietà di applicazioni pratiche. Questa guida dettagliata ti fornirà gli strumenti e le conoscenze necessarie per determinare la base di un parallelogramma, indipendentemente dalle informazioni di cui disponi.

Comprendere il Parallelogramma

Prima di addentrarci nei metodi di calcolo, è fondamentale definire cosa sia un parallelogramma. Un parallelogramma è un quadrilatero (una figura a quattro lati) con due coppie di lati opposti paralleli e uguali. Questo significa che i lati opposti non solo sono paralleli, ma hanno anche la stessa lunghezza. Le sue proprietà lo distinguono da altre figure geometriche come rettangoli (che hanno angoli retti) e rombi (che hanno quattro lati uguali).

Proprietà Chiave di un Parallelogramma

Per calcolare la base, è utile conoscere le seguenti proprietà:

I lati opposti sono paralleli e congruenti (uguali in lunghezza).
Gli angoli opposti sono congruenti.
Gli angoli adiacenti sono supplementari (sommano a 180 gradi).
Le diagonali si bisecano (si intersecano nel loro punto medio).

Metodi per Trovare la Base di un Parallelogramma

Esistono diversi metodi per calcolare la base di un parallelogramma, a seconda delle informazioni che hai a disposizione. Esploreremo i metodi più comuni.

1. Utilizzo dell'Area e dell'Altezza

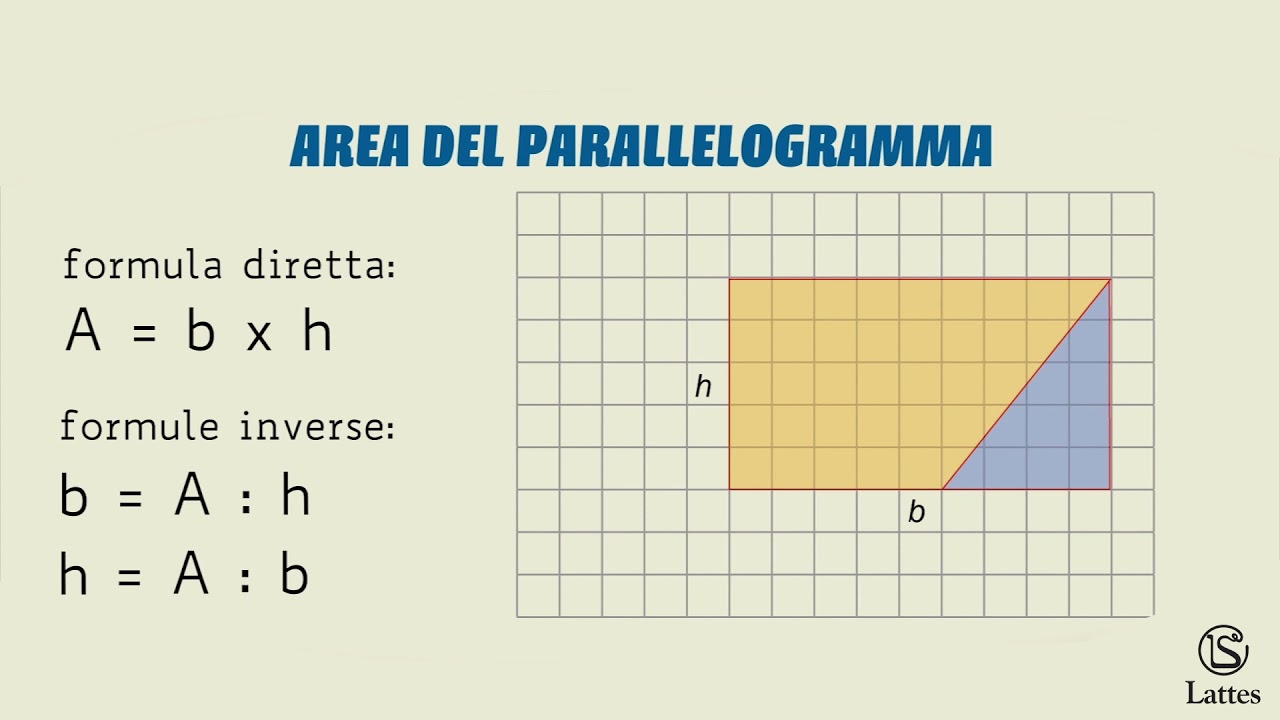
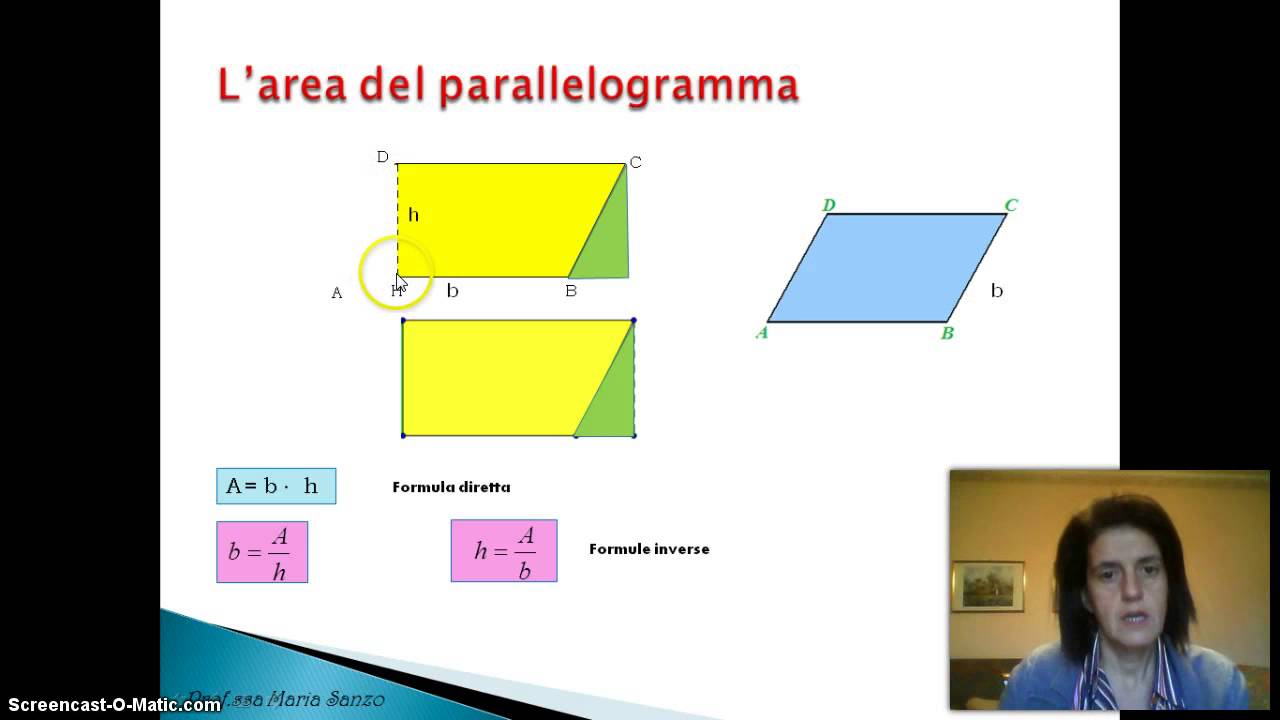
Il metodo più diretto, se conosci l'area (A) e l'altezza (h) del parallelogramma, è utilizzare la formula fondamentale:

A = b * h

Dove:

A = Area del parallelogramma
b = Lunghezza della base
h = Altezza del parallelogramma (la distanza perpendicolare tra la base e il lato opposto)

Per trovare la base (b), basta riorganizzare la formula:

b = A / h

In pratica, se un parallelogramma ha un'area di 50 cm² e un'altezza di 5 cm, la sua base sarà:

b = 50 cm² / 5 cm = 10 cm

2. Utilizzo della Lunghezza dei Lati e dell'Angolo

Se conosci la lunghezza di un lato adiacente alla base (chiamiamolo 'a') e l'angolo (θ) tra la base e quel lato, puoi utilizzare la trigonometria. L'altezza (h) può essere calcolata come:

h = a * sin(θ)

Una volta calcolata l'altezza, puoi usare la formula dell'area (A = b * h) per trovare la base (b), se conosci l'area, oppure la relazione trigonometrica di base per trovare l'area se conosci la base.

Supponiamo di conoscere l'area (A) e di aver calcolato h. Allora:

b = A / h

Se non conosci l'area ma conosci la lunghezza di un altro lato, 'a', e l'angolo tra la base e 'a', 'θ', puoi utilizzare la seguente formula per calcolare l'area: A = a * b * sin(θ). Se conosci a e θ, puoi trovare l'area (A) in funzione di 'b': A = k * b, dove k = a * sin(θ).

3. Utilizzo delle Coordinate dei Vertici

Se hai le coordinate dei vertici del parallelogramma in un piano cartesiano, puoi calcolare la lunghezza della base utilizzando la formula della distanza. Scegli due vertici adiacenti che formano la base e applica la formula:

Siano (x1, y1) e (x2, y2) le coordinate dei due vertici.

b = √((x2 - x1)² + (y2 - y1)²)

Questa formula deriva dal teorema di Pitagora e ti fornisce la distanza tra i due punti, che corrisponde alla lunghezza della base. È importante scegliere i due vertici che definiscono effettivamente un lato del parallelogramma, e non una diagonale.

4. Utilizzo delle Diagonali e dell'Angolo tra Loro

Questo metodo è meno comune, ma se conosci le lunghezze delle diagonali (d1 e d2) e l'angolo (α) tra di esse, puoi utilizzare una formula più complessa per calcolare l'area, e da lì, se conosci l'altezza, trovare la base. Tuttavia, questo metodo raramente viene utilizzato direttamente per trovare la base; di solito si usa per calcolare l'area.

L'area del parallelogramma è data da:

A = (1/2) * d1 * d2 * sin(α)

Per usare questo metodo per trovare la base è necessario conoscere anche l'altezza.

Esempi Pratici e Applicazioni Reali

I parallelogrammi e il calcolo della loro base trovano applicazione in molti settori. Ecco alcuni esempi:

Architettura: Nella progettazione di edifici, i parallelogrammi possono essere utilizzati per creare design unici e resistenti. Conoscere la base è fondamentale per calcolare i materiali necessari.
Ingegneria: Nel calcolo delle forze agenti su una struttura, spesso si scompongono le forze in componenti parallele. I parallelogrammi di forze aiutano a visualizzare e calcolare queste componenti.
Design grafico: Nella creazione di loghi o elementi grafici, i parallelogrammi possono essere utilizzati per aggiungere dinamismo e interesse visivo.
Matematica e Fisica: Lo studio dei parallelogrammi è fondamentale per comprendere concetti più avanzati come i vettori e la geometria analitica.
Agricoltura: I campi possono essere a volte approssimati con parallelogrammi per calcolare l'area coltivabile, o per ottimizzare la disposizione delle colture.

Ad esempio, immagina un architetto che deve progettare una finestra a forma di parallelogramma. Conoscendo l'altezza della finestra (diciamo 1 metro) e l'area desiderata (diciamo 1.5 metri quadrati), può facilmente calcolare la base utilizzando la formula b = A / h. In questo caso, la base sarebbe di 1.5 metri.

Un altro esempio potrebbe essere un agricoltore che ha un campo a forma di parallelogramma. Misurando la base (diciamo 100 metri) e l'altezza (diciamo 50 metri), può calcolare l'area del campo (A = b * h = 5000 metri quadrati) e stimare la quantità di fertilizzante necessaria.

Errori Comuni da Evitare

Quando si calcola la base di un parallelogramma, è importante evitare alcuni errori comuni:

Confondere l'altezza con la lunghezza del lato obliquo: L'altezza è sempre la distanza perpendicolare tra la base e il lato opposto.
Utilizzare unità di misura incoerenti: Assicurati che tutte le misure siano espresse nella stessa unità (es. metri, centimetri).
Applicare formule errate: Scegli la formula appropriata in base alle informazioni disponibili.
Ignorare le proprietà del parallelogramma: Ricorda che i lati opposti sono paralleli e uguali.

Conclusione

Calcolare la base di un parallelogramma è un'abilità fondamentale con applicazioni in vari campi. Conoscendo le proprietà del parallelogramma e le formule appropriate, puoi determinare la base in modo preciso e efficiente. Sperimenta con diversi esempi e problemi per affinare le tue capacità. La matematica non è solo teoria, ma uno strumento potente per risolvere problemi reali. Non aver paura di metterti alla prova e di esplorare le infinite possibilità che la geometria offre. Impara, pratica e applica!