Come Si Trova Il Punto Medio

Trovare il punto medio tra due punti è un concetto fondamentale in matematica, geometria e numerose applicazioni pratiche. Che si tratti di dividere un segmento di linea in due parti uguali, calcolare il centro di un oggetto o determinare la posizione "media" tra due coordinate, la capacità di individuare il punto medio è uno strumento prezioso. Questo articolo esplorerà i metodi per trovare il punto medio, fornendo una comprensione chiara e dettagliata del processo.
Comprendere il Concetto di Punto Medio
Il punto medio è, per definizione, il punto che si trova esattamente a metà strada tra due punti dati. Immagina di avere un segmento di linea. Il punto medio è il punto su quella linea che divide il segmento in due segmenti congruenti, ovvero due segmenti di uguale lunghezza. Questo concetto si applica sia in una dimensione (su una retta numerica) che in due o tre dimensioni (in un piano cartesiano o nello spazio).
Punto Medio su una Retta Numerica
Il caso più semplice è trovare il punto medio tra due numeri su una retta numerica. Se hai due numeri, a e b, il punto medio è semplicemente la loro media aritmetica. La formula è:
Punto Medio = (a + b) / 2
Ad esempio, se vuoi trovare il punto medio tra 3 e 7, applichi la formula: (3 + 7) / 2 = 10 / 2 = 5. Quindi, 5 è il punto medio tra 3 e 7.
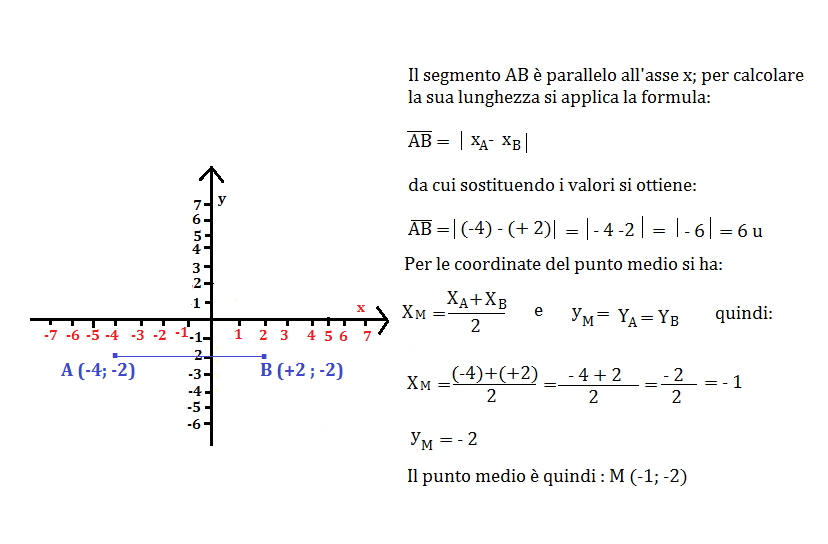
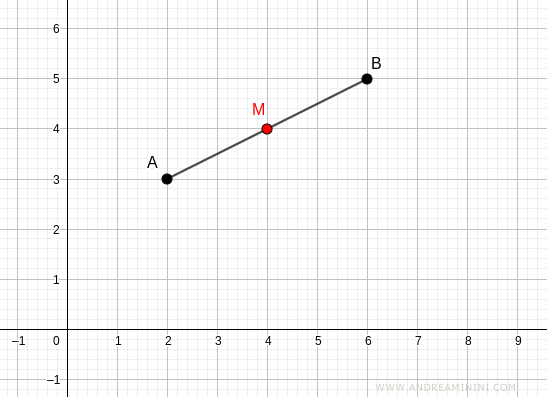
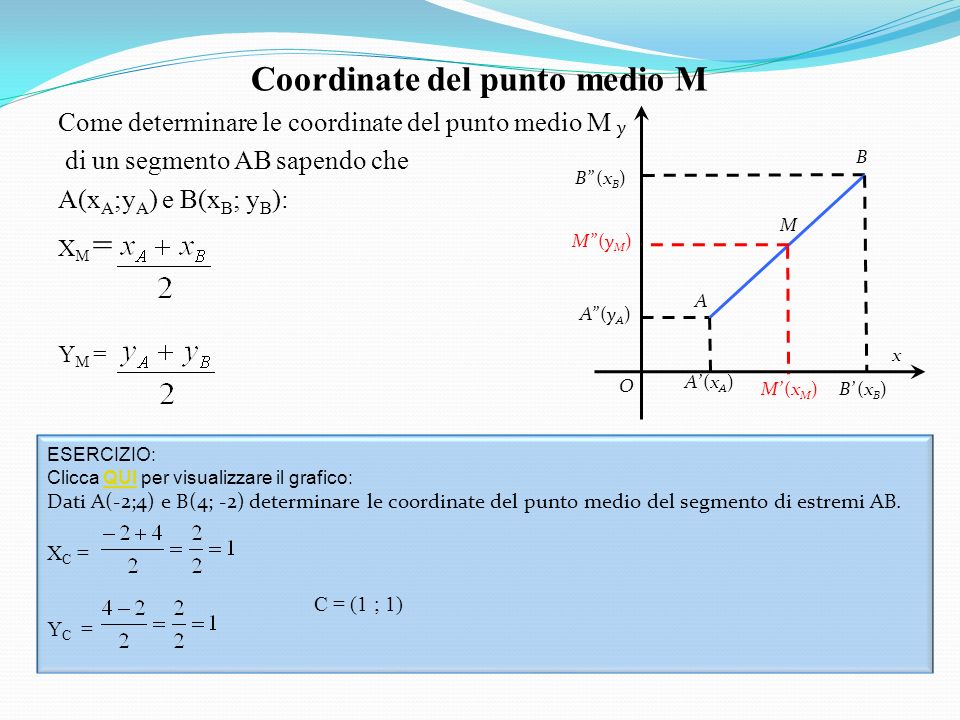
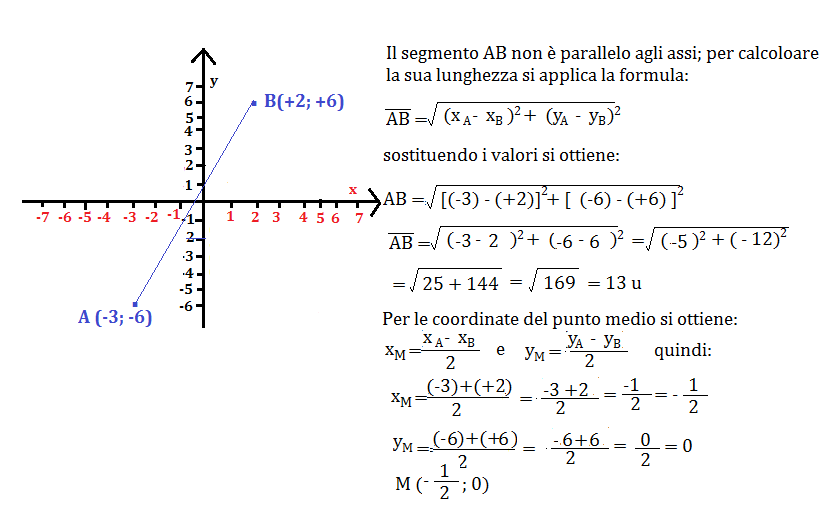
Punto Medio nel Piano Cartesiano (2D)
Le cose si fanno leggermente più complesse quando ci spostiamo in due dimensioni. Nel piano cartesiano, un punto è definito da due coordinate: (x, y). Per trovare il punto medio tra due punti (x1, y1) e (x2, y2), dobbiamo trovare la media delle coordinate x e la media delle coordinate y separatamente.
La formula per trovare il punto medio nel piano cartesiano è:
Punto Medio = ((x1 + x2) / 2, (y1 + y2) / 2)
In altre parole, sommi le coordinate x dei due punti, dividi per 2, e ottieni la coordinata x del punto medio. Fai la stessa cosa per le coordinate y. Il risultato è un nuovo punto (x, y) che rappresenta il punto medio.
Punto Medio nello Spazio (3D)
Il concetto si estende naturalmente a tre dimensioni. Invece di avere solo coordinate x e y, abbiamo anche una coordinata z. Per trovare il punto medio tra due punti (x1, y1, z1) e (x2, y2, z2) nello spazio, seguiamo la stessa logica di prima, calcolando la media di ciascuna coordinata.
La formula per trovare il punto medio nello spazio è:
Punto Medio = ((x1 + x2) / 2, (y1 + y2) / 2, (z1 + z2) / 2)
Esempi Pratici e Applicazioni Reali
La ricerca del punto medio non è solo un esercizio matematico astratto; ha numerose applicazioni nel mondo reale.
- Geolocalizzazione e Mappe: Le applicazioni di mappe utilizzano il concetto di punto medio per calcolare la posizione approssimativa tra due punti di riferimento. Ad esempio, se hai due indirizzi, l'app può stimare un punto di incontro a metà strada.
- Grafica Computerizzata: Nella grafica computerizzata, il punto medio è utilizzato per disegnare linee e curve. Gli algoritmi di rasterizzazione spesso sfruttano il punto medio per determinare quali pixel devono essere colorati per creare una linea liscia.
- Ingegneria e Architettura: Gli ingegneri e gli architetti utilizzano il punto medio per calcolare il centro di massa di una struttura o per dividere uno spazio in parti uguali.
- Statistica: Anche se non è la media statistica, il concetto di "punto medio" si può estendere a intervalli di dati per trovare il valore centrale.
- Navigazione Marittima: I navigatori possono usare il punto medio tra due boe per mantenere una rotta sicura.
Esempio Numerico: Supponiamo di voler trovare il punto medio tra le città di Roma (coordinate approssimative: 41.9028° N, 12.4964° E) e Milano (coordinate approssimative: 45.4654° N, 9.1859° E). Approssimando la Terra come piatta su questa piccola scala, possiamo applicare la formula del punto medio in 2D:
Latitudine del punto medio: (41.9028 + 45.4654) / 2 = 43.6841° N
Longitudine del punto medio: (12.4964 + 9.1859) / 2 = 10.84115° E
Questo posiziona il punto medio approssimativamente nell'area di Parma, in Italia.
Considerazioni Importanti
Sebbene il calcolo del punto medio sia relativamente semplice, ci sono alcune considerazioni da tenere a mente:
Precisione delle Coordinate
La precisione del punto medio dipende dalla precisione delle coordinate di partenza. Se le coordinate di partenza sono approssimative, anche il punto medio sarà approssimativo. Ad esempio, nell'esempio di Roma e Milano, abbiamo usato coordinate approssimative; un calcolo più preciso richiederebbe coordinate più accurate.
Sistemi di Coordinate
È importante assicurarsi che le coordinate di partenza siano nello stesso sistema di coordinate. Ad esempio, non si può mescolare coordinate geografiche (latitudine e longitudine) con coordinate cartesiane. È necessario convertire tutte le coordinate allo stesso sistema prima di calcolare il punto medio.
Applicazioni Geodetiche
Per distanze più lunghe sulla superficie terrestre, la curvatura della Terra diventa significativa. In questi casi, è necessario utilizzare formule geodetiche più complesse per calcolare il punto medio, poiché la Terra non è piatta. Queste formule tengono conto della forma ellissoidale della Terra.
Strumenti e Risorse Online
Esistono numerosi strumenti e risorse online che possono aiutarti a trovare il punto medio. Questi strumenti spesso consentono di inserire le coordinate e calcolano automaticamente il punto medio. Alcuni strumenti offrono anche funzionalità aggiuntive, come la visualizzazione del punto medio su una mappa.
Alcuni esempi includono:
- Calcolatori Online: Molti siti web offrono calcolatori di punto medio che puoi usare gratuitamente. Basta cercare "calcolatore punto medio" su un motore di ricerca.
- Software di Mappatura: Software come Google Maps o ArcGIS possono calcolare il punto medio tra due posizioni.
- Librerie di Programmazione: Se sei un programmatore, puoi usare librerie di programmazione che forniscono funzioni per calcolare il punto medio in vari sistemi di coordinate.
Conclusione e Passi Successivi
La capacità di trovare il punto medio è una competenza matematica di base con applicazioni ampie e diversificate. Che tu stia risolvendo problemi di geometria, sviluppando applicazioni di mappatura o semplicemente cercando un punto di incontro conveniente con un amico, la formula del punto medio è uno strumento prezioso.
Ora che hai compreso i concetti e le formule, ti invito a sperimentare con diversi esempi. Prova a calcolare il punto medio tra diversi punti nel piano cartesiano, nello spazio e sulla retta numerica. Esplora strumenti e risorse online per semplificare il processo. Con la pratica, diventerai abile nell'individuare il punto medio in qualsiasi situazione.
Ricorda: La matematica è un'abilità che si affina con la pratica! Non aver paura di sperimentare e applicare le tue conoscenze a problemi reali. Buona fortuna!